
Weingarten equations
Encyclopedia
Weingarten equations give expansion of the derivative of the unit normal vector to a surface in terms of the first derivatives of the position vector of this surface. These formulas were established in 1861 by German mathematician Julius Weingarten
.
that is parametrized by position vector r(u, v) of the surface. Let P = P(u, v) be a fixed point on this surface. Then
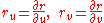
are the tangent vectors at point P.
Let n be the unit normal vector
and let (E, F, G) and (L, M, N) be the coefficients of the first
and second fundamental forms of this surface, respectively. The Weingarten equation gives the first derivative of the unit normal vector n at point P in terms of tangent vectors ru and rv:
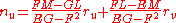
Julius Weingarten
Julius Weingarten was a German mathematician. He made some important contributions to the differential geometry of surfaces, such as theWeingarten equations.-External links:...
.
Statement in classical differential geometry
Let S be a surface in three-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
that is parametrized by position vector r(u, v) of the surface. Let P = P(u, v) be a fixed point on this surface. Then
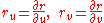
are the tangent vectors at point P.
Let n be the unit normal vector
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
and let (E, F, G) and (L, M, N) be the coefficients of the first
First fundamental form
In differential geometry, the first fundamental form is the inner product on the tangent space of a surface in three-dimensional Euclidean space which is induced canonically from the dot product of R3. It permits the calculation of curvature and metric properties of a surface such as length and...
and second fundamental forms of this surface, respectively. The Weingarten equation gives the first derivative of the unit normal vector n at point P in terms of tangent vectors ru and rv:
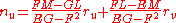
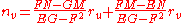
Sources
- Springer Encyclopedia of Mathematics, http://eom.springer.de/w/w097620.htm
- Erwin KreyszigErwin KreyszigErwin O. Kreyszig was a Professor of Mathematics at Carleton University in Ottawa, Canada. He was a pioneer in the field of applied mathematics: non-wave replicating linear systems...
, Differential Geometry, Dover Publications, 1991, ISBN 0-486-66721-9, section 45.

