
Weingarten function
Encyclopedia
In mathematics, Weingarten functions are rational function
s indexed by partitions of integers that can be used to calculate integrals of products of matrix coefficients over classical group
s. They were first studied by who found their asymptotic behavior, and named by , who evaluated them explicitly for the unitary group
.
Ud
of products of matrix coefficients of the form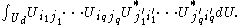
(Here denotes the conjugate transpose of
denotes the conjugate transpose of  , alternatively denoted as
, alternatively denoted as 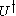 .)
.)
This integral is equal to
where Wg is the Weingarten function, given by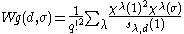
where the sum is over all partitions λ of q . Here χλ is the character if Sq corresponding to the partition λ and s is the Schur polynomial
of λ, so that sλd(1) is the dimension of the representation of Ud corresponding to λ.
The Weingarten functions are rational functions in d. They can have poles for small values of d, which cancel out in the formula above. There is an alternative inequivalent definition of Weingarten functions, where one only sums over partitions with at most d parts. This is no longer a rational function of d, but is finite for all positive integers d. The two sorts of Weingarten functions coincide for d larger than q, and either can be used in the formula for the integral.
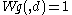 (The trivial case where q = 0)
(The trivial case where q = 0)

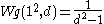

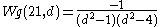

where permutations σ are denoted by their cycle shapes.
There exists a computer algebra program to produce these expressions.
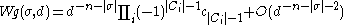
where the permutation σ is a product of cycles of lengths Ci, and cn = (2n)!/n!(n + 1)! is a Catalan number
, and |σ| is the smallest number of transpositions that σ is a product of. There exists a diagrammatic method to systematically calculate the integrals over the unitary group as a power series in 1/d.
and symplectic group
s the Weingarten functions were evaluated by . Their theory is similar to the case of the unitary group. They are parameterized by partitions such that all parts have even size.
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s indexed by partitions of integers that can be used to calculate integrals of products of matrix coefficients over classical group
Classical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
s. They were first studied by who found their asymptotic behavior, and named by , who evaluated them explicitly for the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
.
Unitary groups
Weingarten functions are used for evaluating integrals over the unitary groupUnitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
Ud
of products of matrix coefficients of the form
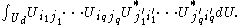
(Here
 denotes the conjugate transpose of
denotes the conjugate transpose of  , alternatively denoted as
, alternatively denoted as 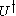 .)
.)This integral is equal to

where Wg is the Weingarten function, given by
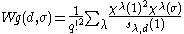
where the sum is over all partitions λ of q . Here χλ is the character if Sq corresponding to the partition λ and s is the Schur polynomial
Schur polynomial
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
of λ, so that sλd(1) is the dimension of the representation of Ud corresponding to λ.
The Weingarten functions are rational functions in d. They can have poles for small values of d, which cancel out in the formula above. There is an alternative inequivalent definition of Weingarten functions, where one only sums over partitions with at most d parts. This is no longer a rational function of d, but is finite for all positive integers d. The two sorts of Weingarten functions coincide for d larger than q, and either can be used in the formula for the integral.
Examples
The first few Weingarten functions Wg(σd) are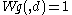 (The trivial case where q = 0)
(The trivial case where q = 0)

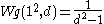

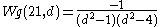

where permutations σ are denoted by their cycle shapes.
There exists a computer algebra program to produce these expressions.
Asymptotic behavior
For large d, the Weingarten function Wg has the asymptotic behavior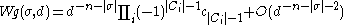
where the permutation σ is a product of cycles of lengths Ci, and cn = (2n)!/n!(n + 1)! is a Catalan number
Catalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
, and |σ| is the smallest number of transpositions that σ is a product of. There exists a diagrammatic method to systematically calculate the integrals over the unitary group as a power series in 1/d.
Orthogonal and symplectic groups
For orthogonalOrthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
and symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
s the Weingarten functions were evaluated by . Their theory is similar to the case of the unitary group. They are parameterized by partitions such that all parts have even size.

