Weyl's inequality in number theory

In number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

, Weyl's inequality, named for Hermann Weyl

Hermann Weyl

Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...

, states that if M, N, a and q are integers, with a and q coprime

Coprime

In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...

, q > 0, and f is a real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

 of degree k whose leading coefficient c satisfies


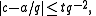
for some t greater than or equal to 1, then for any positive real number 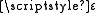one has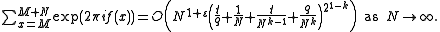


This inequality will only be useful when


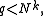
for otherwise estimating the modulus of the exponential sum

Exponential sum

In mathematics, an exponential sum may be a finite Fourier series , or other finite sum formed using the exponential function, usually expressed by means of the functione = \exp.\,...

 by means of the triangle inequality

Triangle inequality

In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....

 as provides a better bound.

Weyl's inequality in matrix theory

In linear algebra, Weyl's inequality is a theorem about the changes to eigenvalues of a Hermitian matrix that is perturbed. It is useful if we wish to know the eigenvalues of the Hermitian matrix H but there is an uncertainty about the entries of H. We let H be the exact matrix and P be a perturbation matrix that represents the uncertainty. The matrix we 'measure' is .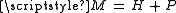

The theorem says that if M, H and P are all n by n Hermitian matrices, where M has eigenvalues


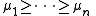
and H has eigenvalues


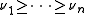
and P has eigenvalues


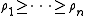
then the following inequalties hold for :


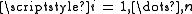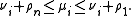
If P is positive definite (e.g. 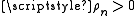) then this implies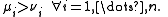


Note that we can order the eigenvalues because the matrices are Hermitian and therefore the eigenvalues are real.