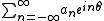Weyl differintegral
Encyclopedia
In mathematics
, the Weyl integral is an operator defined, as an example of fractional calculus
, on functions f on the unit circle
having integral 0 and a Fourier series
. In other words there is a Fourier series for f of the form
with a0 = 0.
Then the Weyl integral operator of order s is defined on Fourier series by
where this is defined. Here s can take any real value, and for integer values k of s the series expansion is the expected k-th derivative, if k > 0, or (−k)th indefinite integral normalized by integration from θ = 0.
The condition a0 = 0 here plays the obvious role of excluding the need to consider division by zero. The definition is due to Hermann Weyl
(1917).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Weyl integral is an operator defined, as an example of fractional calculus
Fractional calculus
Fractional calculus is a branch of mathematical analysis that studies the possibility of taking real number powers or complex number powers of the differentiation operator.and the integration operator J...
, on functions f on the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
having integral 0 and a Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. In other words there is a Fourier series for f of the form
with a0 = 0.
Then the Weyl integral operator of order s is defined on Fourier series by
where this is defined. Here s can take any real value, and for integer values k of s the series expansion is the expected k-th derivative, if k > 0, or (−k)th indefinite integral normalized by integration from θ = 0.
The condition a0 = 0 here plays the obvious role of excluding the need to consider division by zero. The definition is due to Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
(1917).