Whitney extension theorem
Encyclopedia
In mathematics
, in particular in mathematical analysis
, the Whitney extension theorem is a partial converse to Taylor's theorem
. Roughly speaking, the theorem asserts that if A is a closed subset of a Euclidean space, then it is possible to extend a given function off A in such a way as to have prescribed derivatives at the points of A. It is a result of Hassler Whitney
. A related result is due to McShane, hence it is sometimes called the McShane–Whitney extension theorem.
Given a real-valued Cm function f(x) on Rn, Taylor's theorem asserts that for each a, x, y ∈ Rn, it is possible to write
where α is a multi-index and Rα(x,y) → 0 uniformly as x,y → a.
Let fα=Dαf for each multi-index α. Differentiating (1) with respect to x, and possibly replacing R as needed, yields
where Rα is o(|x-y|m-|α|) uniformly as x,y → a.
Note that (2) may be regarded as purely a compatibility condition between the functions fα which must be satisfied in order for these functions to be the coefficients of the Taylor series of the function f. It is this insight which facilitates the following statement
Theorem. Suppose that fα are a collection of functions on a closed subset A of Rn for all multi-indices α with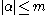
satisfying the compatibility condition (2) at all points x, y, and a of A. Then there exists a function F(x) of class Cm such that:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, the Whitney extension theorem is a partial converse to Taylor's theorem
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
. Roughly speaking, the theorem asserts that if A is a closed subset of a Euclidean space, then it is possible to extend a given function off A in such a way as to have prescribed derivatives at the points of A. It is a result of Hassler Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
. A related result is due to McShane, hence it is sometimes called the McShane–Whitney extension theorem.
Statement
A precise statement of the theorem requires careful consideration of what it means to prescribe the derivative of a function on a closed set. One difficulty, for instance, is that closed subsets of Euclidean space in general lack a differentiable structure. The starting point, then, is an examination of the statement of Taylor's theorem.Given a real-valued Cm function f(x) on Rn, Taylor's theorem asserts that for each a, x, y ∈ Rn, it is possible to write
-
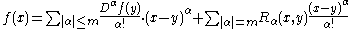(1)
where α is a multi-index and Rα(x,y) → 0 uniformly as x,y → a.
Let fα=Dαf for each multi-index α. Differentiating (1) with respect to x, and possibly replacing R as needed, yields
-
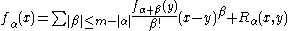(2)
where Rα is o(|x-y|m-|α|) uniformly as x,y → a.
Note that (2) may be regarded as purely a compatibility condition between the functions fα which must be satisfied in order for these functions to be the coefficients of the Taylor series of the function f. It is this insight which facilitates the following statement
Theorem. Suppose that fα are a collection of functions on a closed subset A of Rn for all multi-indices α with
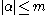satisfying the compatibility condition (2) at all points x, y, and a of A. Then there exists a function F(x) of class Cm such that:
- F=f0 on A.
- DαF = fα on A.
- F is real-analytic at every point of Rn-A.