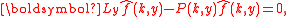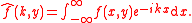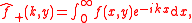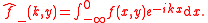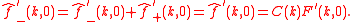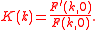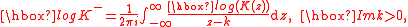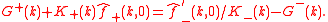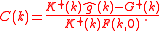Wiener-Hopf
Encyclopedia
The Wiener–Hopf method is a mathematical technique widely used in applied mathematics
. It was initially developed by Norbert Wiener
and Eberhard Hopf
as a method to solve systems of integral equation
s, but has found wider use in solving two-dimensional partial differential equation
s with mixed boundary conditions on the same boundary. In general, the method works by exploiting the complex-analytical
properties of transformed functions. Typically, the standard Fourier transform
is used, but examples exist using other transforms, such as the Mellin transform
.
In general, the governing equations and boundary conditions are transformed and these transforms are used to define a pair of complex functions (typically denoted with '+' and '-' subscripts) which are respectively analytic
in the upper and lower halves of the complex plane, and have growth no faster than polynomials in these regions. These two functions will also coincide on some region of the complex plane
, typically, a thin strip containing the real line
. Analytic continuation
guarantees that these two functions define a single function analytic in the entire complex plane, and Liouville's theorem
implies that this function is an unknown polynomial
, which is often zero or constant. Analysis of the conditions at the edges and corners of the boundary allows one to determine the degree of this polynomial.
 into two functions
into two functions 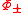 with the desired properties outlined above. In general, this can be done by writing
with the desired properties outlined above. In general, this can be done by writing
and
where the contours and
and  are parallel to the real line, but pass above and below the point
are parallel to the real line, but pass above and below the point  , respectively.
, respectively.
Similarly, arbitrary scalar functions may be decomposed into a product of +/- functions, i.e. , by first taking the logarithm, and then performing a sum decomposition. Product decompositions of matrix functions (which occur in coupled multi-modal systems such as elastic waves) are considerably more problematic since the logarithm is not well defined, and any decomposition might be expected to be non-commutative. A small subclass of commutative decompositions were obtained by Khrapkov, and various approximate methods have also been developed.
, by first taking the logarithm, and then performing a sum decomposition. Product decompositions of matrix functions (which occur in coupled multi-modal systems such as elastic waves) are considerably more problematic since the logarithm is not well defined, and any decomposition might be expected to be non-commutative. A small subclass of commutative decompositions were obtained by Khrapkov, and various approximate methods have also been developed.
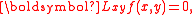
where is a linear operator which contains
is a linear operator which contains
derivatives with respect to and
and 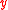 ,
,
subject to the mixed conditions on , for some prescribed
, for some prescribed
function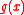 ,
,
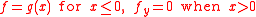
and decay at infinity i.e. as
as  . Taking a Fourier transform
. Taking a Fourier transform
with respect to x results in the following ordinary differential equation
where is a linear operator containing
is a linear operator containing 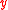 derivatives only,
derivatives only, 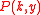 is a known function of
is a known function of 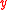 and
and  and
and
If a particular solution of this ordinary differential equation which satisfies the necessary decay at infinity is denoted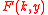 , a general solution can be written as
, a general solution can be written as
where is an unknown function to be determined by the boundary conditions on
is an unknown function to be determined by the boundary conditions on  .
.
The key idea is to split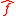 into two separate functions,
into two separate functions, 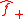 and
and 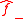 which are analytic in the lower- and upper-halves of the complex plane, respectively
which are analytic in the lower- and upper-halves of the complex plane, respectively
The boundary conditions then give
and, on taking derivatives with respect to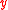 ,
,
Eliminating yields
yields
where
Now can be decomposed into the product of functions
can be decomposed into the product of functions  and
and 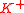 which are analytic in the upper and lower half-planes respectively. To be precise,
which are analytic in the upper and lower half-planes respectively. To be precise, 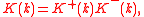 where
where
(Note that this sometimes involves scaling so that it tends to
so that it tends to 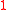 as
as  .) We also decompose
.) We also decompose  into the sum of two functions
into the sum of two functions 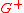 and
and 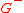 which are analytic in the lower and upper half-planes respectively - i.e.,
which are analytic in the lower and upper half-planes respectively - i.e.,
This can be done in the same way that we factorised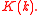
Consequently,
Now, as the left-hand side of the above equation is analytic in the lower half-plane, whilst the right-hand side is analytic in the upper half-plane, analytic continution guarantees existence of an entire function which coincides with the left- or right-hand sides in their respective half-planes. Furthermore, since it can be shown that the functions on either side of the above equation decay at large , an application of Liouville's theorem
, an application of Liouville's theorem
shows that this entire function is identically zero, therefore
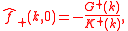
and so
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
. It was initially developed by Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
and Eberhard Hopf
Eberhard Hopf
Eberhard Frederich Ferdinand Hopf was a mathematician and astronomer, one of the founding fathers of ergodic theory and a pioneer of bifurcation theory who also made significant contributions to the subjects of partial differential equations and integral equations, fluid dynamics, and differential...
as a method to solve systems of integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s, but has found wider use in solving two-dimensional partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s with mixed boundary conditions on the same boundary. In general, the method works by exploiting the complex-analytical
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
properties of transformed functions. Typically, the standard Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
is used, but examples exist using other transforms, such as the Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
.
In general, the governing equations and boundary conditions are transformed and these transforms are used to define a pair of complex functions (typically denoted with '+' and '-' subscripts) which are respectively analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
in the upper and lower halves of the complex plane, and have growth no faster than polynomials in these regions. These two functions will also coincide on some region of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, typically, a thin strip containing the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
. Analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
guarantees that these two functions define a single function analytic in the entire complex plane, and Liouville's theorem
Liouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
implies that this function is an unknown polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, which is often zero or constant. Analysis of the conditions at the edges and corners of the boundary allows one to determine the degree of this polynomial.
Wiener–Hopf decomposition
The key step in many Wiener–Hopf problems is to decompose an arbitrary function into two functions
into two functions 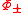 with the desired properties outlined above. In general, this can be done by writing
with the desired properties outlined above. In general, this can be done by writingand
where the contours
 and
and  are parallel to the real line, but pass above and below the point
are parallel to the real line, but pass above and below the point  , respectively.
, respectively.Similarly, arbitrary scalar functions may be decomposed into a product of +/- functions, i.e.
 , by first taking the logarithm, and then performing a sum decomposition. Product decompositions of matrix functions (which occur in coupled multi-modal systems such as elastic waves) are considerably more problematic since the logarithm is not well defined, and any decomposition might be expected to be non-commutative. A small subclass of commutative decompositions were obtained by Khrapkov, and various approximate methods have also been developed.
, by first taking the logarithm, and then performing a sum decomposition. Product decompositions of matrix functions (which occur in coupled multi-modal systems such as elastic waves) are considerably more problematic since the logarithm is not well defined, and any decomposition might be expected to be non-commutative. A small subclass of commutative decompositions were obtained by Khrapkov, and various approximate methods have also been developed.Example
Let us consider the linear partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
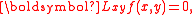
where
 is a linear operator which contains
is a linear operator which containsderivatives with respect to
 and
and 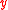 ,
,subject to the mixed conditions on
 , for some prescribed
, for some prescribedfunction
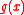 ,
,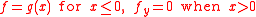
and decay at infinity i.e.
 as
as  . Taking a Fourier transform
. Taking a Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
with respect to x results in the following ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
where
 is a linear operator containing
is a linear operator containing 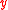 derivatives only,
derivatives only, 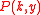 is a known function of
is a known function of 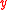 and
and  and
andIf a particular solution of this ordinary differential equation which satisfies the necessary decay at infinity is denoted
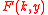 , a general solution can be written as
, a general solution can be written aswhere
 is an unknown function to be determined by the boundary conditions on
is an unknown function to be determined by the boundary conditions on  .
.The key idea is to split
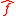 into two separate functions,
into two separate functions, 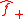 and
and 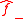 which are analytic in the lower- and upper-halves of the complex plane, respectively
which are analytic in the lower- and upper-halves of the complex plane, respectivelyThe boundary conditions then give
and, on taking derivatives with respect to
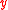 ,
,Eliminating
 yields
yieldswhere
Now
 can be decomposed into the product of functions
can be decomposed into the product of functions  and
and 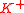 which are analytic in the upper and lower half-planes respectively. To be precise,
which are analytic in the upper and lower half-planes respectively. To be precise, 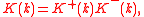 where
where(Note that this sometimes involves scaling
 so that it tends to
so that it tends to 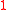 as
as  .) We also decompose
.) We also decompose  into the sum of two functions
into the sum of two functions 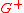 and
and 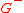 which are analytic in the lower and upper half-planes respectively - i.e.,
which are analytic in the lower and upper half-planes respectively - i.e.,
This can be done in the same way that we factorised
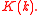
Consequently,
Now, as the left-hand side of the above equation is analytic in the lower half-plane, whilst the right-hand side is analytic in the upper half-plane, analytic continution guarantees existence of an entire function which coincides with the left- or right-hand sides in their respective half-planes. Furthermore, since it can be shown that the functions on either side of the above equation decay at large
 , an application of Liouville's theorem
, an application of Liouville's theoremLiouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
shows that this entire function is identically zero, therefore
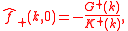
and so
External links
- Wiener–Hopf method at Wikiwaves