Witt vector
Encyclopedia
In mathematics
, a Witt vector is an infinite sequence of elements of a commutative ring
. Ernst Witt
showed how to put a ring structure
on the set of Witt vectors, in such a way that the ring of Witt vectors over the finite field of order p is the ring of p-adic integers.
a0 + a1p1 + a2p2 + ... where the as are usually taken from the set {0, 1, 2, ..., p − 1}. This set of representatives is not the only possible choice, and Teichmüller
suggested an alternative set consisting of 0 together with the p − 1st roots of 1: in other words, the p roots of
These Teichmüller representatives can be identified with the elements of the finite field
Fp of order p (by taking residues mod p), so this identifies the set of p-adic integers with infinite sequences of elements of Fp.
We now have the following problem: given two infinite sequences of elements of Fp, identified with p-adic integers using Teichmüller's representatives, describe their sum and product as p-adic integers explicitly. This problem was solved by Witt using Witt vectors.
p. A Witt vector over a commutative ring R is a sequence (X0, X1,X2,...) of elements of R. Define the Witt polynomials Wi by
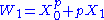
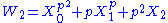
and in general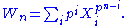
Then Witt showed that there is a unique way to make the set of Witt vectors over any commutative ring R into a ring, called the ring of Witt vectors, such that
The first few polynomials giving the sum and product of Witt vectors can be written down explicitly. For example, + (Y0, Y1,...) = (X0+Y0, X1 + Y1 + (X0p + Y0p − (X0 + Y0)p)/p, ...) × (Y0, Y1,...) = (X0Y0, X0pY1 + Y0pX1 + p X1Y1, ...)
Define the universal Witt polynomials Wn for n≥1 by
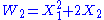
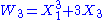
and in general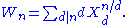
We can use these polynomials to define the ring of universal Witt vectors over any commutative ring R in much the same way as above (so the universal Witt polynomials are all homomorphisms to the ring R).
from commutative rings to commutative rings, and is also representable, so it can be thought of as a ring scheme, called the Witt scheme, over Spec(Z). The Witt scheme can be canonically identified with the spectrum of the ring of symmetric functions.
Similarly the rings of truncated Witt vectors, and the rings of
universal Witt vectors, correspond to ring schemes, called the truncated Witt schemes and the universal Witt scheme .
Moreover, the functor taking the commutative ring R to the set Rn is represented by the affine space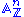
, and the ring structure on Rn makes 
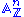into a ring scheme denoted 
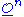. From the construction of truncated Witt vectors it follows that their associated ring scheme 
is the scheme 
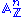with the unique ring structure such that the morphism 
given by the Witt polynomials is a morphism of ring schemes.
of characteristic 0, any unipotent
abelian connected algebraic group
is isomorphic to a product of copies of the additive group Ga.
The analogue of this for fields of characteristic p is false: the truncated Witt schemes are counterexamples. (We make them into algebraic groups by forgetting the multiplication and just using the additive structure.) However these are essentially the only counterexamples: over an algebraically closed field of characteristic p, any unipotent
abelian connected algebraic group
is
isogenous to a product of truncated Witt group schemes.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Witt vector is an infinite sequence of elements of a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. Ernst Witt
Ernst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
showed how to put a ring structure
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
on the set of Witt vectors, in such a way that the ring of Witt vectors over the finite field of order p is the ring of p-adic integers.
Motivation
Any p-adic integer can be written as a power seriesa0 + a1p1 + a2p2 + ... where the as are usually taken from the set {0, 1, 2, ..., p − 1}. This set of representatives is not the only possible choice, and Teichmüller
Oswald Teichmüller
Oswald Teichmüller was a German mathematician who introduced quasiconformal mappings and differential geometric methods into complex analysis.-Life:...
suggested an alternative set consisting of 0 together with the p − 1st roots of 1: in other words, the p roots of
- xp − x = 0.
These Teichmüller representatives can be identified with the elements of the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
Fp of order p (by taking residues mod p), so this identifies the set of p-adic integers with infinite sequences of elements of Fp.
We now have the following problem: given two infinite sequences of elements of Fp, identified with p-adic integers using Teichmüller's representatives, describe their sum and product as p-adic integers explicitly. This problem was solved by Witt using Witt vectors.
Construction of Witt rings
Fix a prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p. A Witt vector over a commutative ring R is a sequence (X0, X1,X2,...) of elements of R. Define the Witt polynomials Wi by
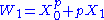
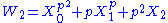
and in general
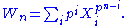
Then Witt showed that there is a unique way to make the set of Witt vectors over any commutative ring R into a ring, called the ring of Witt vectors, such that
- the sum and product are given by polynomials with integral coefficients that do not depend on R, and
- Every Witt polynomial is a homomorphism from the ring of Witt vectors over R to R.
The first few polynomials giving the sum and product of Witt vectors can be written down explicitly. For example, + (Y0, Y1,...) = (X0+Y0, X1 + Y1 + (X0p + Y0p − (X0 + Y0)p)/p, ...) × (Y0, Y1,...) = (X0Y0, X0pY1 + Y0pX1 + p X1Y1, ...)
Examples
- The Witt ring of any commutative ring R in which p is invertible is just isomorphic to RN (the product of a countable number of copies of R). In fact the Witt polynomials always give a homomorphism from the ring of Witt vectors to RN, and if p is invertible this homomorphism is an isomorphism.
- The Witt ring of the finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
of order p is the ring of p-adic integers. - The Witt ring of a finite field of order pn is the unramified extensionSplitting of prime ideals in Galois extensionsIn mathematics, the interplay between the Galois group G of a Galois extension L of a number field K, and the way the prime ideals P of the ring of integers OK factorise as products of prime ideals of OL, provides one of the richest parts of algebraic number theory...
of degree n of the ring of p-adic integers.
Universal Witt vectors
The Witt polynomials for different primes p are special cases of universal Witt polynomials, which can be used to form a universal Witt ring (not depending on a choice of prime p).Define the universal Witt polynomials Wn for n≥1 by
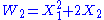
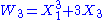
and in general
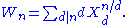
We can use these polynomials to define the ring of universal Witt vectors over any commutative ring R in much the same way as above (so the universal Witt polynomials are all homomorphisms to the ring R).
Ring schemes
The map taking a commutative ring R to the ring of Witt vectors over R (for a fixed prime p) is a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from commutative rings to commutative rings, and is also representable, so it can be thought of as a ring scheme, called the Witt scheme, over Spec(Z). The Witt scheme can be canonically identified with the spectrum of the ring of symmetric functions.
Similarly the rings of truncated Witt vectors, and the rings of
universal Witt vectors, correspond to ring schemes, called the truncated Witt schemes and the universal Witt scheme .
Moreover, the functor taking the commutative ring R to the set Rn is represented by the affine space
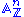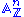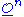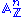, and the ring structure on Rn makes into a ring scheme denoted . From the construction of truncated Witt vectors it follows that their associated ring scheme is the scheme with the unique ring structure such that the morphism given by the Witt polynomials is a morphism of ring schemes.Commutative unipotent algebraic groups
Over an algebraically closed fieldAlgebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
of characteristic 0, any unipotent
Unipotent
In mathematics, a unipotent element r of a ring R is one such that r − 1 is a nilpotent element, in other words such that some power n is zero....
abelian connected algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
is isomorphic to a product of copies of the additive group Ga.
The analogue of this for fields of characteristic p is false: the truncated Witt schemes are counterexamples. (We make them into algebraic groups by forgetting the multiplication and just using the additive structure.) However these are essentially the only counterexamples: over an algebraically closed field of characteristic p, any unipotent
Unipotent
In mathematics, a unipotent element r of a ring R is one such that r − 1 is a nilpotent element, in other words such that some power n is zero....
abelian connected algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
is
isogenous to a product of truncated Witt group schemes.