
Witten zeta function
Encyclopedia
In mathematics, the Witten zeta function, introduced by , is a function associated to a root system
that encodes the degrees of the irreducible representations of the corresponding Lie group
. It is a special case of the Shintani zeta function
.
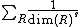
where the sum is over equivalence classes of irreducible representations R.
If Δ of rank r is a root system with n positive roots in Δ+ and with simple roots λi, the Witten zeta function of several variables is given by
The original zeta function studied by Witten differed from this slightly, in that all the numbers sα are equal, and the function is multiplied by a constant.
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
that encodes the degrees of the irreducible representations of the corresponding Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. It is a special case of the Shintani zeta function
Shintani zeta function
In mathematics, a Shintani zeta function or Shintani L-function is a generalization of the Riemann zeta function. They were studied studied by...
.
Definition
Witten's original definition of the zeta function of a semisimple Lie group was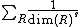
where the sum is over equivalence classes of irreducible representations R.
If Δ of rank r is a root system with n positive roots in Δ+ and with simple roots λi, the Witten zeta function of several variables is given by

The original zeta function studied by Witten differed from this slightly, in that all the numbers sα are equal, and the function is multiplied by a constant.

