Wrapped Lévy distribution
Encyclopedia
In probability theory
and directional statistics, a wrapped Lévy distribution is a wrapped probability distribution
that results from the "wrapping" of the Lévy distribution around the unit circle
.
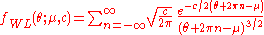
where the value of the summand is taken to be zero when
, 
is the scale factor and 
is the location parameter. Expressing
the above pdf in terms of the characteristic function
of the Lévy distribution yields:
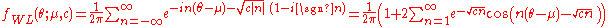
In terms of the circular variable
the circular moments of the wrapped Lévy distribution are the characteristic function of the Lévy distribution evaluated at integer arguments:
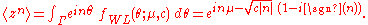
where
is some interval of length 
. The first moment is then the expectation value of z, also known as the mean resultant, or mean resultant vector:
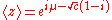
The mean angle is
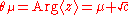
and the length of the mean resultant is
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and directional statistics, a wrapped Lévy distribution is a wrapped probability distribution
Wrapped distribution
In probability theory and directional statistics, a wrapped probability distribution is a continuous probability distribution that describes data points that lie on a unit n-sphere...
that results from the "wrapping" of the Lévy distribution around the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
.
Description
The pdf of the wrapped Lévy distribution is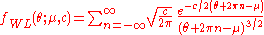where the value of the summand is taken to be zero when
, is the scale factor and is the location parameter. ExpressingWrapped distribution
In probability theory and directional statistics, a wrapped probability distribution is a continuous probability distribution that describes data points that lie on a unit n-sphere...
the above pdf in terms of the characteristic function
Characteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
of the Lévy distribution yields:
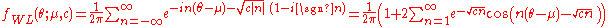
In terms of the circular variable
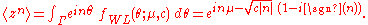
the circular moments of the wrapped Lévy distribution are the characteristic function of the Lévy distribution evaluated at integer arguments:where
is some interval of length . The first moment is then the expectation value of z, also known as the mean resultant, or mean resultant vector: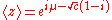The mean angle is
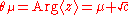
and the length of the mean resultant is