
Wythoff's game
Encyclopedia
Wythoff's game is a two-player mathematical
game of strategy, played with two piles of counters. Players take turns removing counters from one or both piles; in the latter case, the numbers of counters removed from each pile must be equal. The game ends when one person removes the last counter or counters, thus winning.
Martin Gardner
claims that the game was played in China under the name 捡石子 jiǎn shízǐ ("picking stones"). The Dutch mathematician W. A. Wythoff
published a mathematical analysis of the game in 1907.
The classification of positions into hot and cold can be carried out recursively
with the following three rules:
For instance, all positions of the form (0, m) and (m, m) with m > 0 are hot, by rule 2. However, the position (1,2) is cold, because the only positions that can be reached from it, (0,1), (0,2), and (1,1), are all hot. The cold positions (n, m) with the smallest values of n and m are (0, 0), (1, 2), (3, 5), (4, 7),(6,10) and (8, 13).
. Specifically, if k is any natural number and
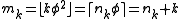
where φ is the golden ratio and we are using the floor function
, then (nk, mk) is the kth cold position. These two sequences of numbers are recorded in the Online Encyclopedia of Integer Sequences as and , respectively.
The two sequences nk and mk are the Beatty sequence
s associated with the equation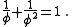
As is true in general for pairs of Beatty sequences, these two sequences are complementary
: each positive integer appears exactly once in either sequence.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
game of strategy, played with two piles of counters. Players take turns removing counters from one or both piles; in the latter case, the numbers of counters removed from each pile must be equal. The game ends when one person removes the last counter or counters, thus winning.
Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
claims that the game was played in China under the name 捡石子 jiǎn shízǐ ("picking stones"). The Dutch mathematician W. A. Wythoff
Willem Abraham Wythoff
Willem Abraham Wythoff was a Dutch mathematician and number theorist. Wythoff is well-known for his study of a combinatorial game referred to as Wythoff's game and for the Wythoff construction and the Wythoff symbol utilised in this tiling construction.- References :*...
published a mathematical analysis of the game in 1907.
Optimal strategy
Any position in the game can be described by a pair of integers (n, m) with n ≤ m, describing the size of both piles in the position. The strategy of the game revolves around cold positions and hot positions: in a cold position, the player whose turn it is to move will lose with best play, while in a hot position, the player whose turn it is to move will win with best play. The optimal strategy from a hot position is to move to any reachable cold position.The classification of positions into hot and cold can be carried out recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
with the following three rules:
- (0,0) is a cold position.
- Any position from which a cold position can be reached in a single move is a hot position.
- If every move leads to a hot position, then a position is cold.
For instance, all positions of the form (0, m) and (m, m) with m > 0 are hot, by rule 2. However, the position (1,2) is cold, because the only positions that can be reached from it, (0,1), (0,2), and (1,1), are all hot. The cold positions (n, m) with the smallest values of n and m are (0, 0), (1, 2), (3, 5), (4, 7),(6,10) and (8, 13).
Formula for cold positions
Wythoff discovered that the cold positions follow a regular pattern determined by the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. Specifically, if k is any natural number and

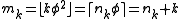
where φ is the golden ratio and we are using the floor function
Floor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
, then (nk, mk) is the kth cold position. These two sequences of numbers are recorded in the Online Encyclopedia of Integer Sequences as and , respectively.
The two sequences nk and mk are the Beatty sequence
Beatty sequence
In mathematics, a Beatty sequence is the sequence of integers found by taking the floor of the positive multiplesof a positive irrational number...
s associated with the equation
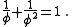
As is true in general for pairs of Beatty sequences, these two sequences are complementary
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
: each positive integer appears exactly once in either sequence.

