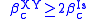XY model
Encyclopedia
The classical XY model
is a model of statistical mechanics
. It is the special case of the n-vector model for .
.
 -dimensional lattice
-dimensional lattice  , per each lattice site
, per each lattice site  there is a two-dimensional, unit-length vector
there is a two-dimensional, unit-length vector
 . A spin configuration,
. A spin configuration,  is an assignment of the angle
is an assignment of the angle 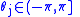 per each site
per each site  in the lattice.
in the lattice.
Given a translation-invariant interaction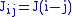 and a point dependent external field
and a point dependent external field
 , the configuration energy is
, the configuration energy is
The case in which except for
except for 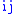 nearest neighbor is called 'nearest neighbor case'.
nearest neighbor is called 'nearest neighbor case'.
The configuration probability is given by the Boltzmann distribution
with inverse temperature :
:
where is the normalization, or partition function
is the normalization, or partition function
.
is a model of statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. It is the special case of the n-vector model for
 .
.Definition
Given a -dimensional lattice
-dimensional lattice  , per each lattice site
, per each lattice site  there is a two-dimensional, unit-length vector
there is a two-dimensional, unit-length vector . A spin configuration,
. A spin configuration,  is an assignment of the angle
is an assignment of the angle 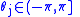 per each site
per each site  in the lattice.
in the lattice.Given a translation-invariant interaction
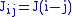 and a point dependent external field
and a point dependent external field , the configuration energy is
, the configuration energy is
The case in which
 except for
except for 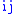 nearest neighbor is called 'nearest neighbor case'.
nearest neighbor is called 'nearest neighbor case'.The configuration probability is given by the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
with inverse temperature
 :
:
where
 is the normalization, or partition function
is the normalization, or partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
.
General properties
- The existence of the thermodynamic limit for the free energyThermodynamic free energyThe thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
and spin correlations were proved by GinibreJean GinibreJean Ginibre is a French mathematical physicist, known in particular for his contributions to random matrix theory , statistical mechanics , and partial differential equations. He received the Paul Langevin Prize in 1969.Jean Ginibre is Emeritus Professor at Paris-Sud 11 University....
, extending to this case the Griffiths inequalityGriffiths inequalityIn statistical mechanics, the Griffiths inequality , named after Robert B. Griffiths, is a correlation inequality for ferromagnetic spin systems...
.
- At high temperature, the spontaneous magnetization vanishes:
-

- Besides, cluster expansionCluster expansionIn statistical mechanics, the cluster expansion is a power series expansion of the partition function of a statistical field theory around a model that is a union of non-interacting 0-dimensional field theories. Cluster expansions originated in the work of...
shows that the spin correlations cluster exponentially fast: for instance
- Using the Griffiths inequalityGriffiths inequalityIn statistical mechanics, the Griffiths inequality , named after Robert B. Griffiths, is a correlation inequality for ferromagnetic spin systems...
in the formulation of Ginibre, Aizenman and Simon proved that the two point spin correlation of the ferromagnetics XY model in dimension , coupling
, coupling  and inverse temperature
and inverse temperature  is dominated by (i.e. has upper bound given by) the two point correlation of the ferromagnetic Ising modelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
is dominated by (i.e. has upper bound given by) the two point correlation of the ferromagnetic Ising modelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
in dimension , coupling
, coupling  and inverse temperature
and inverse temperature 
-

- Hence the critical
 of the XY model cannot be smaller than the double of the critical temperature of the Ising model
of the XY model cannot be smaller than the double of the critical temperature of the Ising model
One dimension
As in any 'nearest-neighbor' n-vector model with free boundary conditions, if the external field is zero, there exists a simple exact solution.
In the nearest-neighbor, free boundary conditions case, the Hamiltonian is
therefore the partition function factorizes under the change of coordinates
That gives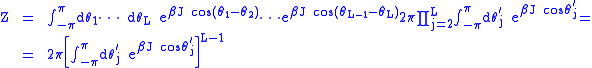
Finally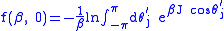
The same computation for periodic boundary condition (and still ) requires the transfer matrix formalism.
) requires the transfer matrix formalism.
Two Dimensions
- At low temperature, the spontaneous magnetization remains zero,
-

- but Fröhlich and Spencer proved that the decay of the correlations is only power law.
 .
.
The continuous version of the XY model is often used to model systems that possess order parameters with the same kinds of symmetry, e.g. superfluid helium, hexatic liquid crystals. This is what makes them peculiar from other phase transitions which are always accompanied with a symmetry breaking. Topological defects in the XY model leads to a vortex-unbinding transition from the low-temperature phase to the high-temperature disordered phase. In two spatial dimensions the XY model exhibits a Kosterlitz-Thouless transitionKosterlitz-Thouless transitionIn statistical mechanics, a part of mathematical physics, the Kosterlitz–Thouless transition, or Berezinsky–Kosterlitz–Thouless transition, is a kind of phase transition that appears in the XY model in 2 spatial dimensions. The XY model is a 2-dimensional vector spin model that possesses U or...
from the disordered high-temperature phase into the quasi-long range ordered low-temperature phase.
Three and Higher Dimensions
- At low temperature, infrared bound shows that the spontaneous magnetization is strictly positive:
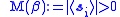
See also
- Goldstone bosonGoldstone bosonIn particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
- Ising modelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
- Potts modelPotts modelIn statistical mechanics, the Potts model, a generalization of the Ising model, is a model of interacting spins on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid state physics...
- Kosterlitz-Thouless transitionKosterlitz-Thouless transitionIn statistical mechanics, a part of mathematical physics, the Kosterlitz–Thouless transition, or Berezinsky–Kosterlitz–Thouless transition, is a kind of phase transition that appears in the XY model in 2 spatial dimensions. The XY model is a 2-dimensional vector spin model that possesses U or...
- Topological defectTopological defectIn mathematics and physics, a topological soliton or a topological defect is a solution of a system of partial differential equations or of a quantum field theory homotopically distinct from the vacuum solution; it can be proven to exist because the boundary conditions entail the existence of...
- Superfluid filmSuperfluid filmSuperfluidity and superconductivity are macroscopic manifestations of quantum mechanics. There is considerable interest, both theoretical and practical, in these quantum phase transitions. There has been a tremendous amount of work done in the field of phase transitions and critical phenomenon in...
- At low temperature, infrared bound shows that the spontaneous magnetization is strictly positive:
- but Fröhlich and Spencer proved that the decay of the correlations is only power law.
- Hence the critical
- Using the Griffiths inequality
- Besides, cluster expansion