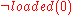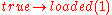Yale shooting problem
Encyclopedia
The Yale shooting problem is a conundrum or scenario in formal situational logic
on which early logical solutions to the frame problem
fail. The name of this problem derives from its inventors, Steve Hanks and Drew McDermott
, working at Yale University
when they proposed it. In this scenario, Fred (later identified as a turkey
) is initially alive and a gun is initially unloaded. Loading the gun, waiting for a moment, and then shooting the gun at Fred is expected to kill Fred. However, if inertia
is formalized in logic by minimizing the changes in this situation, then it cannot be uniquely proved that Fred is dead after loading, waiting, and shooting. In one solution, Fred indeed dies; in another (also logically correct) solution, the gun becomes mysteriously unloaded and Fred survives.
Technically, this scenario is described by two fluents
(a fluent is a condition that can change truth value over time):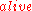 and
and 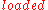 . Initially, the first condition is true and the second is false. Then, the gun is loaded, some time passes, and the gun is fired. Such problems can be formalized in logic by considering four time points
. Initially, the first condition is true and the second is false. Then, the gun is loaded, some time passes, and the gun is fired. Such problems can be formalized in logic by considering four time points  ,
,  ,
,  , and
, and  , and turning every fluent such as
, and turning every fluent such as 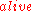 into a predicate
into a predicate 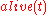 depending on time. A direct formalization of the statement of the Yale shooting problem in logic is the following one:
depending on time. A direct formalization of the statement of the Yale shooting problem in logic is the following one:
The first two formulae represent the initial state. The third formula formalizes the effect of loading the gun at time . The fourth formula formalizes the effect of shooting at Fred at time
. The fourth formula formalizes the effect of shooting at Fred at time 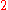 . This is a simplified formalization in which action names are neglected and the effects of actions are directly specified for the time points in which the actions are executed. See situation calculus
. This is a simplified formalization in which action names are neglected and the effects of actions are directly specified for the time points in which the actions are executed. See situation calculus
for details.
The formulae above, while being direct formalizations of the known facts, do not suffice to correctly characterize the domain. Indeed,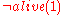 is consistent with all these formulae, although there is no reason to believe that Fred dies before the gun has been shot. The problem is that the formulae above only include the effects of actions, but do not specify that all fluents not changed by the actions remain the same. In other words, a formula
is consistent with all these formulae, although there is no reason to believe that Fred dies before the gun has been shot. The problem is that the formulae above only include the effects of actions, but do not specify that all fluents not changed by the actions remain the same. In other words, a formula  must be added to formalize the implicit assumption that loading the gun only changes the value of
must be added to formalize the implicit assumption that loading the gun only changes the value of 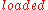 and not the value of
and not the value of 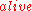 . The necessity of a large number of formulae stating the obvious fact that conditions do not change unless an action changes them is known as the frame problem
. The necessity of a large number of formulae stating the obvious fact that conditions do not change unless an action changes them is known as the frame problem
.
An early solution to the frame problem was based on minimizing the changes. In other words, the scenario is formalized by the formulae above (that specify only the effects of actions) and by the assumption that the changes in the fluents over time are as minimal as possible. The rationale is that the formulae above enforce all effect of actions to take place, while minimization should restrict the changes to exactly those due to the actions.
In the Yale shooting scenario, one possible evaluation of the fluents in which the changes are minimized is the following one.
This is the expected solution. It contains two fluent changes: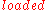 becomes true at time 1 and
becomes true at time 1 and 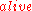 becomes false at time 3. The following evaluation also satisfies all formulae above.
becomes false at time 3. The following evaluation also satisfies all formulae above.
In this evaluation, there are still two changes only: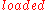 becomes true at time 1 and false at time 2. As a result, this evaluation is considered a valid description of the evolution of the state, although there is no valid reason to explain
becomes true at time 1 and false at time 2. As a result, this evaluation is considered a valid description of the evolution of the state, although there is no valid reason to explain 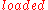 being false at time 2. The fact that minimization of changes leads to wrong solution is the motivation for the introduction of the Yale shooting problem.
being false at time 2. The fact that minimization of changes leads to wrong solution is the motivation for the introduction of the Yale shooting problem.
While the Yale shooting problem has been considered a severe obstacle to the use of logic for formalizing dynamical scenarios, solutions to it are known since the late 1980s. One solution involves the use of predicate completion in the specification of actions: according to this solution, the fact that shooting causes Fred to die is formalized by the preconditions: alive and loaded, and the effect is that alive changes value (since alive was true before, this corresponds to alive becoming false). By turning this implication into an if and only if statement, the effects of shooting are correctly formalized. (Predicate completion is more complicated when there is more than one implication involved.)
A solution proposed by Erik Sandewall
was to include a new condition of occlusion, which formalizes the “permission to change” for a fluent. The effect of an action that might change a fluent is therefore that the fluent has the new value, and that the occlusion is made (temporarily) true. What is minimized is not the set of changes, but the set of occlusions being true. Another constraint specifying that no fluent changes unless occlusion is true completes this solution.
The Yale shooting scenario is also correctly formalized by the Reiter version of the situation calculus
, the fluent calculus
, and the action description language
s.
In spite of being a solved problem, the Yale shooting scenario is still sometimes mentioned in recent research papers, where it is used as an illustrative example (e.g., for explaining the syntax of a new logic for reasoning about actions), rather than being presented as a problem.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
on which early logical solutions to the frame problem
Frame problem
In artificial intelligence, the frame problem was initially formulated as the problem of expressing a dynamical domain in logic without explicitly specifying which conditions are not affected by an action. John McCarthy and Patrick J. Hayes defined this problem in their 1969 article, Some...
fail. The name of this problem derives from its inventors, Steve Hanks and Drew McDermott
Drew McDermott
Drew McDermott is a Professor of Computer Science at Yale University. He was born in 1949, and lived in the Midwestern United States , for four years, and in Brazil .-Education:...
, working at Yale University
Yale University
Yale University is a private, Ivy League university located in New Haven, Connecticut, United States. Founded in 1701 in the Colony of Connecticut, the university is the third-oldest institution of higher education in the United States...
when they proposed it. In this scenario, Fred (later identified as a turkey
Turkey (bird)
A turkey is a large bird in the genus Meleagris. One species, Meleagris gallopavo, commonly known as the Wild Turkey, is native to the forests of North America. The domestic turkey is a descendant of this species...
) is initially alive and a gun is initially unloaded. Loading the gun, waiting for a moment, and then shooting the gun at Fred is expected to kill Fred. However, if inertia
Inertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
is formalized in logic by minimizing the changes in this situation, then it cannot be uniquely proved that Fred is dead after loading, waiting, and shooting. In one solution, Fred indeed dies; in another (also logically correct) solution, the gun becomes mysteriously unloaded and Fred survives.
Technically, this scenario is described by two fluents
Fluent (artificial intelligence)
In artificial intelligence, a fluent is a condition that can change over time. In logical approaches to reasoning about actions, fluents can be represented in first-order logic by predicates having an argument that depends on time...
(a fluent is a condition that can change truth value over time):
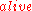 and
and 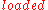 . Initially, the first condition is true and the second is false. Then, the gun is loaded, some time passes, and the gun is fired. Such problems can be formalized in logic by considering four time points
. Initially, the first condition is true and the second is false. Then, the gun is loaded, some time passes, and the gun is fired. Such problems can be formalized in logic by considering four time points  ,
,  ,
,  , and
, and  , and turning every fluent such as
, and turning every fluent such as 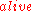 into a predicate
into a predicate 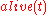 depending on time. A direct formalization of the statement of the Yale shooting problem in logic is the following one:
depending on time. A direct formalization of the statement of the Yale shooting problem in logic is the following one:The first two formulae represent the initial state. The third formula formalizes the effect of loading the gun at time
 . The fourth formula formalizes the effect of shooting at Fred at time
. The fourth formula formalizes the effect of shooting at Fred at time 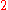 . This is a simplified formalization in which action names are neglected and the effects of actions are directly specified for the time points in which the actions are executed. See situation calculus
. This is a simplified formalization in which action names are neglected and the effects of actions are directly specified for the time points in which the actions are executed. See situation calculusSituation calculus
The situation calculus is a logic formalism designed for representing and reasoning about dynamical domains. It was first introduced by John McCarthy in 1963. The main version of the situational calculus that is presented in this article is based on that introduced by Ray Reiter in 1991...
for details.
The formulae above, while being direct formalizations of the known facts, do not suffice to correctly characterize the domain. Indeed,
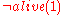 is consistent with all these formulae, although there is no reason to believe that Fred dies before the gun has been shot. The problem is that the formulae above only include the effects of actions, but do not specify that all fluents not changed by the actions remain the same. In other words, a formula
is consistent with all these formulae, although there is no reason to believe that Fred dies before the gun has been shot. The problem is that the formulae above only include the effects of actions, but do not specify that all fluents not changed by the actions remain the same. In other words, a formula  must be added to formalize the implicit assumption that loading the gun only changes the value of
must be added to formalize the implicit assumption that loading the gun only changes the value of 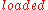 and not the value of
and not the value of 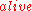 . The necessity of a large number of formulae stating the obvious fact that conditions do not change unless an action changes them is known as the frame problem
. The necessity of a large number of formulae stating the obvious fact that conditions do not change unless an action changes them is known as the frame problemFrame problem
In artificial intelligence, the frame problem was initially formulated as the problem of expressing a dynamical domain in logic without explicitly specifying which conditions are not affected by an action. John McCarthy and Patrick J. Hayes defined this problem in their 1969 article, Some...
.
An early solution to the frame problem was based on minimizing the changes. In other words, the scenario is formalized by the formulae above (that specify only the effects of actions) and by the assumption that the changes in the fluents over time are as minimal as possible. The rationale is that the formulae above enforce all effect of actions to take place, while minimization should restrict the changes to exactly those due to the actions.
In the Yale shooting scenario, one possible evaluation of the fluents in which the changes are minimized is the following one.
 |
 |
 |
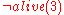 |
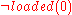 |
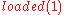 |
 |
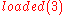 |
This is the expected solution. It contains two fluent changes:
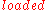 becomes true at time 1 and
becomes true at time 1 and 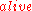 becomes false at time 3. The following evaluation also satisfies all formulae above.
becomes false at time 3. The following evaluation also satisfies all formulae above.  |
 |
 |
 |
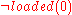 |
 |
 |
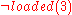 |
In this evaluation, there are still two changes only:
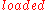 becomes true at time 1 and false at time 2. As a result, this evaluation is considered a valid description of the evolution of the state, although there is no valid reason to explain
becomes true at time 1 and false at time 2. As a result, this evaluation is considered a valid description of the evolution of the state, although there is no valid reason to explain 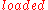 being false at time 2. The fact that minimization of changes leads to wrong solution is the motivation for the introduction of the Yale shooting problem.
being false at time 2. The fact that minimization of changes leads to wrong solution is the motivation for the introduction of the Yale shooting problem.While the Yale shooting problem has been considered a severe obstacle to the use of logic for formalizing dynamical scenarios, solutions to it are known since the late 1980s. One solution involves the use of predicate completion in the specification of actions: according to this solution, the fact that shooting causes Fred to die is formalized by the preconditions: alive and loaded, and the effect is that alive changes value (since alive was true before, this corresponds to alive becoming false). By turning this implication into an if and only if statement, the effects of shooting are correctly formalized. (Predicate completion is more complicated when there is more than one implication involved.)
A solution proposed by Erik Sandewall
Erik Sandewall
Erik Sandewall is a Swedish Professor in the Chair of Computer Science at Linköping University since 1975. He is known for his pioneering research in artificial intelligence.- Education :Erik Sandewall received the B.A. and Ph.D...
was to include a new condition of occlusion, which formalizes the “permission to change” for a fluent. The effect of an action that might change a fluent is therefore that the fluent has the new value, and that the occlusion is made (temporarily) true. What is minimized is not the set of changes, but the set of occlusions being true. Another constraint specifying that no fluent changes unless occlusion is true completes this solution.
The Yale shooting scenario is also correctly formalized by the Reiter version of the situation calculus
Situation calculus
The situation calculus is a logic formalism designed for representing and reasoning about dynamical domains. It was first introduced by John McCarthy in 1963. The main version of the situational calculus that is presented in this article is based on that introduced by Ray Reiter in 1991...
, the fluent calculus
Fluent calculus
The fluent calculus is a formalism for expressing dynamical domains in first-order logic. It is a variant of the situation calculus; the main difference is that situations are considered representations of states. A binary function symbol \circ is used to concatenate the terms that represent facts...
, and the action description language
Action description language
In artificial intelligence, Action description language is an automated planning and scheduling system in particular for robots. It is considered an advancement of STRIPS. Pednault proposed this language in 1987...
s.
In spite of being a solved problem, the Yale shooting scenario is still sometimes mentioned in recent research papers, where it is used as an illustrative example (e.g., for explaining the syntax of a new logic for reasoning about actions), rather than being presented as a problem.