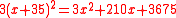Yigu yanduan is a 13th-century mathematical work by Yuan dynasty

Yuan Dynasty

The Yuan Dynasty , or Great Yuan Empire was a ruling dynasty founded by the Mongol leader Kublai Khan, who ruled most of present-day China, all of modern Mongolia and its surrounding areas, lasting officially from 1271 to 1368. It is considered both as a division of the Mongol Empire and as an...

 mathematician Li Zhi

Li Zhi (mathematician)

Li Zhi , later Li Ye , was a Chinese mathematician and scholar, who published and improved the tian yuan shu method for solving polynomial equations of one variable.- Name :...

. Yigu yanduan was based on North Song mathematician Jiang Zhou (蒋周) Yigu Ji (益古集 Collection of Old Mathematics)which was extinct. However from fragments quoted in Yang Hui

Yang Hui

Yang Hui , courtesy name Qianguang , was a Chinese mathematician from Qiantang , Zhejiang province during the late Song Dynasty . Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting 'Yang Hui's Triangle'...

's work The Complete Agorithms of Acreage(田亩比类算法大全), we know that this lost mathematic treatise Yigu Ji was about solving area problems with geometry. Li Zhi used the examples of Yigu Ji to introduce the art of Tian yuan shu

Tian yuan shu

' is a Chinese system of algebra for polynomial equations created in the 13th century. It is first known from the writing of Li Zhi , though it was created earlier....

 to new comers to this field. Although Li Zhi's previous monograph Ceyuan haijing also used tian yuan shu, however it is harder to understand than Yigu yanduan.

Yigu yanduan was later collected into Siku Quanshu

Siku Quanshu

The Siku Quanshu, variously translated as the Imperial Collection of Four, Emperor's Four Treasuries, Complete Library in Four Branches of Literature, or Complete Library of the Four Treasuries, is the largest collection of books in Chinese history and probably the most ambitious editorial...

.

Content

Yigu yanduan consists of three volumes with 64 problems solved with Tian yuan shu

Tian yuan shu

' is a Chinese system of algebra for polynomial equations created in the 13th century. It is first known from the writing of Li Zhi , though it was created earlier....

 in parallel with geometrical method. Li Zhi intended to introduced students to the art of Tian yuan shu thru ancient geometry. Yigu yanduan together with Ceyuan haijing are considered major contribution to Tian yuan shu

Tian yuan shu

' is a Chinese system of algebra for polynomial equations created in the 13th century. It is first known from the writing of Li Zhi , though it was created earlier....

 by Li Zhi. These two works are also considered as the earliest extant documents on Tian yuans shu.

All the 64 problems followed more or less the same format, it started with a question, followed by an answer, a diagram, then a method, in which Li Zhi explaned step by step how to set up algebra equation with Tian yuan shu

Tian yuan shu

' is a Chinese system of algebra for polynomial equations created in the 13th century. It is first known from the writing of Li Zhi , though it was created earlier....

, then followed by geometrical interpretation (Tiao duan shu). The order of arrangement of Tian yuan shu equation in Yigu yanduan is the reverse of that in Ceyuan haijing, i.e., here with the
constant term at top, followed by first order tian yuan, second order tian yuan, third order tian yuan etc. This later arrangement conformed
with contemporary convention of algebra equation( for instance, Qin Jiushao's Mathematical Treatise in Nine Sections

Mathematical Treatise in Nine Sections

The Mathematical Treatise in Nine Sections is a mathematical text written by Chinese Southern Song dynasty mathematician Qin Jiushao in the year 1247.This book contains nine chapters:#Da Yan type ;#Heaven phenomena...

), and later became a norm.

Volume I

Problem 1 to 22, all about the mathematics of a circle embedded in a square.

Example: problem 8

There is a square field, with a circular pool in the middle, given that the land is 13.75 mu, and the sum of the circumferences of the square field and the circular pool equals to 300 steps, what is the circumferences of the square and circle respective ?

Anwwer: The circumference of the square is 240 steps, the circumference of the circle is 60 steps.

Method: set up tian yuan one (celetial element 1) as the diameter of the circle, x

TAI

multiply it by 3 to get the circumference of the circle 3x (pi ~~3)

TAI

subtract this from the sum of circumfereces to obtain the circumference of the square 300-3x

TAI

The square of it equals to 16 times the area of the square (300-3x)*(300-3x) = 900 -1800x +9

TAI

Again set up tian yuan 1 as the diameter of circle, square it up and multiplied by 12 to get
16 times the area of circle as

TAI

subtract from 16 time square area we have 16 times area of land

TAI

put it at right hand side
and put 16 times 13.75 mu = 16 * 13.75 *240 =52800 steps at left,
after cancellation, we get 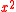=0:

TAI

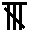
Solve this equation to get diameter of circle = 20 steps, circumference of circle = 60 steps

Volume II

Problem 23 to 42, 20 problems in all solving geometry of rectangle embedded in circle with tian yuan shu

Example, problem 35

Suppose we have a circular field with a rectangular water pool in the center, and the distance of a corner to the circumference is 17.5 steps,
and the sum of length and width of the pool is 85 steps, what is the diameter of the circle, the length and width of the pool ?

Answer: The diameter of the circle is one hundred steps, the length of pool is 60 steps, and the width 25 steps.
Method: Let tian yuan one as the diagonal of rectangle, then the diamter of circle is tian yuan one plus 17.5*2

x+35

multiply the square of diameter with equals to four times the area of the circle:

subracting four times the area of land to obtain:

four times the area of pool = =

now

The square of the sum of length and width of the pool =85*85 =7225
which is four times the pool area plus the square of the difference of its length and width ()

Further
double the pool area plus equals to 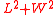= the square of the diagonal of the pool
thus

( four time pool area + the square of its dimension difference ) - (twice the pool area + square if its dimension difference)
equals 7225 - 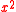= twice the pool area

so four times the area of pool =

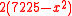
equate this with the four times pool area obtained above

=

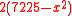we get a quadratic equation =0
Solve this equation to get

• diagonal of pool =65 steps
• diameter of circle =65 +2*17.5 =100 steps
• Length - width =35 steps
• Length + width =85 steps
• Length =60 steps
• Width =25 steps

Volume III

Problem 42 to 64, altogether 22 questions about the mathematics of more complex diagrams