Young–Laplace equation
Encyclopedia
In physics
, the Young–Laplace equation is a nonlinear partial differential equation
that describes the capillary pressure difference sustained across the interface between two static fluids
, such as water
and air, due to the phenomenon of surface tension
or wall tension, although usage on the latter is only applicable if assuming that the wall is very thin. The Young–Laplace equation relates the pressure difference to the shape of the surface or wall and it is fundamentally important in the study of static capillary surface
s. It is a statement of normal stress balance for static fluids meeting at an interface, where the interface is treated as a surface
(zero thickness):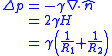
where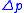 is the pressure difference across the fluid interface, γ is the surface tension
is the pressure difference across the fluid interface, γ is the surface tension
(or wall tension), is the unit normal pointing out of the surface,
is the unit normal pointing out of the surface,  is the mean curvature
is the mean curvature
, and and
and  are the principal radii of curvature
are the principal radii of curvature
. (Some authors refer inappropriately to the factor as the total curvature
as the total curvature
.) Note that only normal stress is considered, this is because it can be shown that a static interface is possible only in the absence of tangential stress.
The equation is named after Thomas Young
, who developed the qualitative theory of surface tension in 1805, and Pierre-Simon Laplace
who completed the mathematical description in the following year. It is sometimes also called the Young–Laplace–Gauss equation, as Gauss
unified the work of Young and Laplace in 1830, deriving both the differential equation and boundary conditions using Johann Bernoulli
's virtual work
principles.
.
. To form the small, highly curved droplets of an emulsion, extra energy is required to overcome the large pressure that results from their small radius.
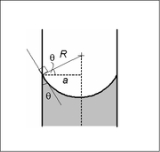
In a sufficiently narrow (i.e., low Bond number) tube of circular cross-section (radius a), the interface between two fluids forms a meniscus
that is a portion of the surface of a sphere with radius R. The pressure jump across this surface is: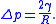
This may be shown by writing the Young–Laplace equation in spherical form with a contact angle
boundary condition and also a prescribed height boundary condition at, say, the bottom of the meniscus. The solution is a portion of a sphere, and the solution will exist only for the pressure difference shown above. This is significant because there isn't another equation or law to specify the pressure difference; existence of solution for one specific value of the pressure difference prescribes it.
The radius of the sphere will be a function only of the contact angle
, θ, which in turn depends on the exact properties of the fluids and the solids in which they are in contact: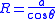
so that the pressure difference may be written as:
 In order to maintain hydrostatic equilibrium
In order to maintain hydrostatic equilibrium
, the induced capillary pressure is balanced by a change in height, h, which can be positive or negative, depending on whether the wetting angle is less than or greater than 90°. For a fluid of density
ρ: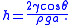 .
.
— where g is the gravitational acceleration
. This is sometimes known as the Jurin rule or Jurin height after James Jurin
who studied the effect in 1718.
For a water-filled glass tube in air at sea level
:
— and so the height of the water column is given by: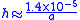 m
m
.
Thus for a 2 mm wide (1 mm radius) tube, the water would rise 14 mm. However, for a capillary tube with radius 0.1 mm, the water would rise 14 cm (about 6 inch
es).

The equation can be non-dimensionalised
in terms of its characteristic length-scale, the capillary length: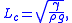
— and characteristic pressure: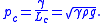
For clean water at standard temperature and pressure, the capillary length is ~2 mm.
The non-dimensional equation then becomes: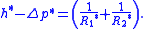
Thus, the surface shape is determined by only one parameter, the over pressure of the fluid, Δp* and the scale of the surface is given by the capillary length. The solution of the equation requires an initial condition for position, and the gradient of the surface at the start point.
 >
>
to give the hydrostatic Young–Laplace equations :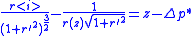
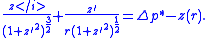
it is often referred to as the Law of Laplace, used in the context of cardiovascular physiology
, and also respiratory physiology
. Arteries may be viewed as cylinders, and the left ventricle of the heart can be viewed as part cylinder, part hemisphere (a bullet shape), modeled by the Law of Laplace as T=p x r / (2 x t), where T=wall tension, p=pressure, r=radius, t=wall thickness. For a given pressure, increased radius requires increased wall thickness to accommodate a stable wall tension; also, increased pressure requires increased thickness to maintain a stable wall tension. The latter is used to explain thickening of arteries and thickening of the left ventricle to accommodate high blood pressure. However, the thickened left ventricle is stiffer than when the thickness is normal, so it requires elevated pressures to fill, a condition known as diastolic heart failure. Note that trucks carrying pressurized gas often have multiple tubes of small radius, so that the wall tension T will be low to reduce need for thick walls to prevent pipes from bursting. The lung contains small spherical gas-exchange chambers called alveoli, where a single alveolus can be modeled as being a perfect sphere. The Law of Laplace explains why alveoli of the lung need small radius to accommodate their thin walls for gas exchange at atmospheric pressure. Numerous small radius alveoli also achieves high surface area
Applying the Law of Laplace to alveoli of the lung, the pressure differential nets a force pushing on the surface of the alveolus, tending to decrease size during exhalation. The Law of Laplace states that there is an inverse relationship between surface tension and alveolar radius. It follows from this that if surface tensions are equal, a small alveolus will experience a greater inward force than a large alveolus. In that case, if both alveoli are connected to the same airway, the small alveolus will be more likely to collapse, expelling its contents into the large alveolus.
This explains why the presence of surfactant
lining the alveoli is of vital importance. Surfactant reduces the surface tension on all alveoli, but its effect is greater on small alveoli than on large alveoli. Thus, surfactant compensates for the size differences between alveoli, and ensures that smaller alveoli do not collapse. You can mimic this issue by connecting two inflated balloons to either ends of a plastic straw or a stiffer tube (you may need rubber bands to secure them). If the balloons are equal in thickness and radius then they can stay equally inflated, but if you squeeze one a bit to reduce its radius, the condition will be unstable, and in accord with the Law of Laplace, the smaller one will empty itself into the larger one.
The Law of Laplace also explains various phenomena encountered in the pathology
of vascular
or gastrointestinal walls
. The wall tension in this case represents the muscular tension
on the wall of the vessel. For example, if an aneurysm
forms in a blood vessel wall, the radius of the vessel has increased. This means that the inward force on the vessel decreases, and therefore the aneurysm will continue to expand until it ruptures. A similar logic applies to the formation of diverticuli in the gut
.
The Law of Laplace can also be used to model transmural pressure in the heart and the rest of the circulatory system.
performed some of the earliest observations and experiments in 1709 and these were repeated in 1718 by James Jurin
who observed that the height of fluid in a capillary column was a function only of the cross-sectional area at the surface, not of any other dimensions of the column.
Thomas Young
laid the foundations of the equation in his 1804 paper An Essay on the Cohesion of Fluids where he set out in descriptive terms the principles governing contact between fluids (along with many other aspects of fluid behaviour). Pierre Simon Laplace followed this up in Mécanique Céleste with the formal mathematical description given above, which reproduced in symbolic terms the relationship described earlier by Young.
Laplace accepted the idea propounded by Hauksbee in the Philosophical Transactions for 1709, that the phenomenon was due to a force of attraction that was insensible at sensible distances. The part which deals with the action of a solid
on a liquid
and the mutual action of two liquids was not worked out thoroughly, but ultimately was completed by Gauss. Carl Neumann
later filled in a few details.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Young–Laplace equation is a nonlinear partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
that describes the capillary pressure difference sustained across the interface between two static fluids
Fluid statics
Fluid statics is the science of fluids at rest, and is a sub-field within fluid mechanics. The term usually refers to the mathematical treatment of the subject. It embraces the study of the conditions under which fluids are at rest in stable equilibrium...
, such as water
Water
Water is a chemical substance with the chemical formula H2O. A water molecule contains one oxygen and two hydrogen atoms connected by covalent bonds. Water is a liquid at ambient conditions, but it often co-exists on Earth with its solid state, ice, and gaseous state . Water also exists in a...
and air, due to the phenomenon of surface tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
or wall tension, although usage on the latter is only applicable if assuming that the wall is very thin. The Young–Laplace equation relates the pressure difference to the shape of the surface or wall and it is fundamentally important in the study of static capillary surface
Capillary surface
In fluid mechanics and mathematics, a capillary surface is a surface that represents the interface between two different fluids. As a consequence of being a surface, a capillary surface has no thickness in slight contrast with most real fluid interfaces....
s. It is a statement of normal stress balance for static fluids meeting at an interface, where the interface is treated as a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
(zero thickness):
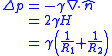
where
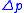 is the pressure difference across the fluid interface, γ is the surface tension
is the pressure difference across the fluid interface, γ is the surface tensionSurface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
(or wall tension),
 is the unit normal pointing out of the surface,
is the unit normal pointing out of the surface,  is the mean curvature
is the mean curvatureMean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
, and
 and
and  are the principal radii of curvature
are the principal radii of curvaturePrincipal curvature
In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.-Discussion:...
. (Some authors refer inappropriately to the factor
 as the total curvature
as the total curvatureTotal curvature
In mathematical study of the differential geometry of curves, the total curvature of an immersed plane curve is the integral of curvature along a curve taken with respect to arclength:\int_a^b k\,ds....
.) Note that only normal stress is considered, this is because it can be shown that a static interface is possible only in the absence of tangential stress.
The equation is named after Thomas Young
Thomas Young (scientist)
Thomas Young was an English polymath. He is famous for having partly deciphered Egyptian hieroglyphics before Jean-François Champollion eventually expanded on his work...
, who developed the qualitative theory of surface tension in 1805, and Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
who completed the mathematical description in the following year. It is sometimes also called the Young–Laplace–Gauss equation, as Gauss
Gauss
Gauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
unified the work of Young and Laplace in 1830, deriving both the differential equation and boundary conditions using Johann Bernoulli
Johann Bernoulli
Johann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
's virtual work
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
principles.
Soap films
If the pressure difference is zero, as in a soap film without gravity, the interface will assume the shape of a minimal surfaceMinimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
.
Emulsions
The equation also explains the energy required to create an emulsionEmulsion
An emulsion is a mixture of two or more liquids that are normally immiscible . Emulsions are part of a more general class of two-phase systems of matter called colloids. Although the terms colloid and emulsion are sometimes used interchangeably, emulsion is used when both the dispersed and the...
. To form the small, highly curved droplets of an emulsion, extra energy is required to overcome the large pressure that results from their small radius.
Capillary pressure in a tube
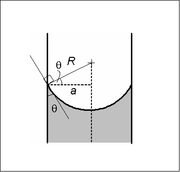 |
In a sufficiently narrow (i.e., low Bond number) tube of circular cross-section (radius a), the interface between two fluids forms a meniscus
Meniscus
The meniscus is the curve in the upper surface of a liquid close to the surface of the container or another object, caused by surface tension. It can be either convex or concave. A convex meniscus occurs when the molecules have a stronger attraction to each other than to the material of the...
that is a portion of the surface of a sphere with radius R. The pressure jump across this surface is:
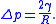
This may be shown by writing the Young–Laplace equation in spherical form with a contact angle
Contact angle
The contact angle is the angle at which a liquid/vapor interface meets a solid surface. The contact angle is specific for any given system and is determined by the interactions across the three interfaces. Most often the concept is illustrated with a small liquid droplet resting on a flat...
boundary condition and also a prescribed height boundary condition at, say, the bottom of the meniscus. The solution is a portion of a sphere, and the solution will exist only for the pressure difference shown above. This is significant because there isn't another equation or law to specify the pressure difference; existence of solution for one specific value of the pressure difference prescribes it.
The radius of the sphere will be a function only of the contact angle
Contact angle
The contact angle is the angle at which a liquid/vapor interface meets a solid surface. The contact angle is specific for any given system and is determined by the interactions across the three interfaces. Most often the concept is illustrated with a small liquid droplet resting on a flat...
, θ, which in turn depends on the exact properties of the fluids and the solids in which they are in contact:
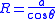
so that the pressure difference may be written as:


Hydrostatic equilibrium
Hydrostatic equilibrium or hydrostatic balance is the condition in fluid mechanics where a volume of a fluid is at rest or at constant velocity. This occurs when compression due to gravity is balanced by a pressure gradient force...
, the induced capillary pressure is balanced by a change in height, h, which can be positive or negative, depending on whether the wetting angle is less than or greater than 90°. For a fluid of density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
ρ:
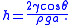 .
.— where g is the gravitational acceleration
Gravitational acceleration
In physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
. This is sometimes known as the Jurin rule or Jurin height after James Jurin
James Jurin
James Jurin FRS MA FRCP MD was an English scientist and physician, particularly remembered for his early work in capillary action and in the epidemiology of smallpox vaccination...
who studied the effect in 1718.
For a water-filled glass tube in air at sea level
Sea level
Mean sea level is a measure of the average height of the ocean's surface ; used as a standard in reckoning land elevation...
:
| γ = 0.0728 J/m2 at 20 °C Celsius Celsius is a scale and unit of measurement for temperature. It is named after the Swedish astronomer Anders Celsius , who developed a similar temperature scale two years before his death... |
θ = 20° (0.35 rad) |
| ρ = 1000 kg/m3 | g = 9.8 m/s2 |
— and so the height of the water column is given by:
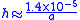 m
mMetre
The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
.
Thus for a 2 mm wide (1 mm radius) tube, the water would rise 14 mm. However, for a capillary tube with radius 0.1 mm, the water would rise 14 cm (about 6 inch
Inch
An inch is the name of a unit of length in a number of different systems, including Imperial units, and United States customary units. There are 36 inches in a yard and 12 inches in a foot...
es).
Capillary action in general
In the general case, for a free surface and where there is an applied "over-pressure", Δp, at the interface in equilibrium, there is a balance between the applied pressure, the hydrostatic pressure and the effects of surface tension. The Young–Laplace equation becomes:
The equation can be non-dimensionalised
Nondimensionalization
Nondimensionalization is the partial or full removal of units from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis...
in terms of its characteristic length-scale, the capillary length:
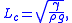
— and characteristic pressure:
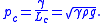
For clean water at standard temperature and pressure, the capillary length is ~2 mm.
The non-dimensional equation then becomes:
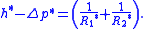
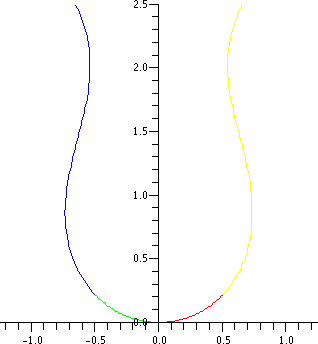
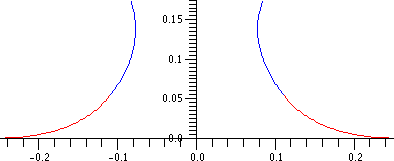
Thus, the surface shape is determined by only one parameter, the over pressure of the fluid, Δp* and the scale of the surface is given by the capillary length. The solution of the equation requires an initial condition for position, and the gradient of the surface at the start point.


Axisymmetric equations
The (nondimensional) shape, r(z) of an axisymmetric surface can be found by substituting general expressions for curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
to give the hydrostatic Young–Laplace equations :
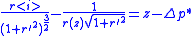
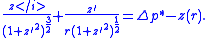
Application in medicine
In medicineMedicine
Medicine is the science and art of healing. It encompasses a variety of health care practices evolved to maintain and restore health by the prevention and treatment of illness....
it is often referred to as the Law of Laplace, used in the context of cardiovascular physiology
Cardiovascular physiology
Cardiovascular physiology is the study of the circulatory system. More specifically, it addresses the physiology of the heart and blood vessels ....
, and also respiratory physiology
Respiratory physiology
Respiratory physiology is the branch of human physiology focusing upon respiration.Topics include:-Volumes:* lung volumes* vital capacity* functional residual capacity* dead space* spirometry* body plethysmography* peak flow meter-Mechanics:...
. Arteries may be viewed as cylinders, and the left ventricle of the heart can be viewed as part cylinder, part hemisphere (a bullet shape), modeled by the Law of Laplace as T=p x r / (2 x t), where T=wall tension, p=pressure, r=radius, t=wall thickness. For a given pressure, increased radius requires increased wall thickness to accommodate a stable wall tension; also, increased pressure requires increased thickness to maintain a stable wall tension. The latter is used to explain thickening of arteries and thickening of the left ventricle to accommodate high blood pressure. However, the thickened left ventricle is stiffer than when the thickness is normal, so it requires elevated pressures to fill, a condition known as diastolic heart failure. Note that trucks carrying pressurized gas often have multiple tubes of small radius, so that the wall tension T will be low to reduce need for thick walls to prevent pipes from bursting. The lung contains small spherical gas-exchange chambers called alveoli, where a single alveolus can be modeled as being a perfect sphere. The Law of Laplace explains why alveoli of the lung need small radius to accommodate their thin walls for gas exchange at atmospheric pressure. Numerous small radius alveoli also achieves high surface area
Applying the Law of Laplace to alveoli of the lung, the pressure differential nets a force pushing on the surface of the alveolus, tending to decrease size during exhalation. The Law of Laplace states that there is an inverse relationship between surface tension and alveolar radius. It follows from this that if surface tensions are equal, a small alveolus will experience a greater inward force than a large alveolus. In that case, if both alveoli are connected to the same airway, the small alveolus will be more likely to collapse, expelling its contents into the large alveolus.
This explains why the presence of surfactant
Pulmonary surfactant
Pulmonary surfactant is a surface-active lipoprotein complex formed by type II alveolar cells. The proteins and lipids that surfactant comprises have both a hydrophilic region and a hydrophobic region...
lining the alveoli is of vital importance. Surfactant reduces the surface tension on all alveoli, but its effect is greater on small alveoli than on large alveoli. Thus, surfactant compensates for the size differences between alveoli, and ensures that smaller alveoli do not collapse. You can mimic this issue by connecting two inflated balloons to either ends of a plastic straw or a stiffer tube (you may need rubber bands to secure them). If the balloons are equal in thickness and radius then they can stay equally inflated, but if you squeeze one a bit to reduce its radius, the condition will be unstable, and in accord with the Law of Laplace, the smaller one will empty itself into the larger one.
The Law of Laplace also explains various phenomena encountered in the pathology
Pathology
Pathology is the precise study and diagnosis of disease. The word pathology is from Ancient Greek , pathos, "feeling, suffering"; and , -logia, "the study of". Pathologization, to pathologize, refers to the process of defining a condition or behavior as pathological, e.g. pathological gambling....
of vascular
Blood vessel
The blood vessels are the part of the circulatory system that transports blood throughout the body. There are three major types of blood vessels: the arteries, which carry the blood away from the heart; the capillaries, which enable the actual exchange of water and chemicals between the blood and...
or gastrointestinal walls
Gastrointestinal tract
The human gastrointestinal tract refers to the stomach and intestine, and sometimes to all the structures from the mouth to the anus. ....
. The wall tension in this case represents the muscular tension
Muscle contraction
Muscle fiber generates tension through the action of actin and myosin cross-bridge cycling. While under tension, the muscle may lengthen, shorten, or remain the same...
on the wall of the vessel. For example, if an aneurysm
Aneurysm
An aneurysm or aneurism is a localized, blood-filled balloon-like bulge in the wall of a blood vessel. Aneurysms can commonly occur in arteries at the base of the brain and an aortic aneurysm occurs in the main artery carrying blood from the left ventricle of the heart...
forms in a blood vessel wall, the radius of the vessel has increased. This means that the inward force on the vessel decreases, and therefore the aneurysm will continue to expand until it ruptures. A similar logic applies to the formation of diverticuli in the gut
Gut (zoology)
In zoology, the gut, also known as the alimentary canal or alimentary tract, is a tube by which bilaterian animals transfer food to the digestion organs. In large bilaterians the gut generally also has an exit, the anus, by which the animal disposes of solid wastes...
.
The Law of Laplace can also be used to model transmural pressure in the heart and the rest of the circulatory system.
History
Francis HauksbeeFrancis Hauksbee
Francis Hauksbee the elder , also known as Francis Hawksbee, was an 18th-century English scientist, and a Fellow of the Royal Society...
performed some of the earliest observations and experiments in 1709 and these were repeated in 1718 by James Jurin
James Jurin
James Jurin FRS MA FRCP MD was an English scientist and physician, particularly remembered for his early work in capillary action and in the epidemiology of smallpox vaccination...
who observed that the height of fluid in a capillary column was a function only of the cross-sectional area at the surface, not of any other dimensions of the column.
Thomas Young
Thomas Young (scientist)
Thomas Young was an English polymath. He is famous for having partly deciphered Egyptian hieroglyphics before Jean-François Champollion eventually expanded on his work...
laid the foundations of the equation in his 1804 paper An Essay on the Cohesion of Fluids where he set out in descriptive terms the principles governing contact between fluids (along with many other aspects of fluid behaviour). Pierre Simon Laplace followed this up in Mécanique Céleste with the formal mathematical description given above, which reproduced in symbolic terms the relationship described earlier by Young.
Laplace accepted the idea propounded by Hauksbee in the Philosophical Transactions for 1709, that the phenomenon was due to a force of attraction that was insensible at sensible distances. The part which deals with the action of a solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
on a liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
and the mutual action of two liquids was not worked out thoroughly, but ultimately was completed by Gauss. Carl Neumann
Carl Neumann
Carl Gottfried Neumann was a German mathematician.Neumann was born in Königsberg, Prussia, as the son of the mineralogist, physicist and mathematician Franz Ernst Neumann , who was professor of mineralogy and physics at Königsberg University...
later filled in a few details.

