Z-factor
Encyclopedia
The Z-factor is a measure of statistical
effect size
. It has been proposed for use in high-throughput screening
to judge whether the response in a particular assay
is large enough to warrant further attention.
samples. The particular choice of experimental conditions and measurements is called an assay. Large screens are expensive in time and resources. Therefore, prior to starting a large screen, smaller test (or pilot) screens are used to assess the quality of an assay, in an attempt to predict if it would be useful in a high-throughput setting. The Z-factor is an attempt to quantify the suitability of a particular assay for use in a full-scale, high-throughput screen.
s and standard deviation
s of both the positive (p) and negative (n) controls (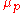
, 
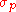, and 
, 
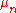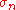). Given these values, the Z-factor is defined as:
In practice, the Z-factor is estimated from the sample mean
s and sample standard deviations
Note that by the standards of many types of experiments, a zero Z-factor would suggest a large effect size, rather than a borderline useless result as suggested above. For example, if σp=σn=1, then μp=6 and μn=0 gives a zero Z-factor. But for normally-distributed data with these parameters, the probability that the positive control value would be less than the negative control value is less than 1 in 105. Extreme conservatism is used in high throughput screening due to the large number of tests performed.
. Extreme values (outliers) in either the positive or negative controls can adversely affect the Z-factor, potentially leading to an apparently favorable Z-factor even when there are severe problems with the assay
.
In addition, the application of the single Z-factor-based criterion to two or more positive controls with different strengths in the same assay will lead to misleading results
. The absolute sign in the Z-factor makes it inconvenient to derive the statistical inference of Z-factor mathematically
. A recently proposed statistical parameter, strictly standardized mean difference (SSMD), can address these issues
. One estimate of SSMD is robust to outliers.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
effect size
Effect size
In statistics, an effect size is a measure of the strength of the relationship between two variables in a statistical population, or a sample-based estimate of that quantity...
. It has been proposed for use in high-throughput screening
High-throughput screening
High-throughput screening is a method for scientific experimentation especially used in drug discovery and relevant to the fields of biology and chemistry. Using robotics, data processing and control software, liquid handling devices, and sensitive detectors, High-Throughput Screening allows a...
to judge whether the response in a particular assay
Assay
An assay is a procedure in molecular biology for testing or measuring the activity of a drug or biochemical in an organism or organic sample. A quantitative assay may also measure the amount of a substance in a sample. Bioassays and immunoassays are among the many varieties of specialized...
is large enough to warrant further attention.
Background
In high-throughput screens, experimenters often compare a large number (hundreds of thousands to tens of millions) of single measurements of unknown samples to positive and negative controlScientific control
Scientific control allows for comparisons of concepts. It is a part of the scientific method. Scientific control is often used in discussion of natural experiments. For instance, during drug testing, scientists will try to control two groups to keep them as identical and normal as possible, then...
samples. The particular choice of experimental conditions and measurements is called an assay. Large screens are expensive in time and resources. Therefore, prior to starting a large screen, smaller test (or pilot) screens are used to assess the quality of an assay, in an attempt to predict if it would be useful in a high-throughput setting. The Z-factor is an attempt to quantify the suitability of a particular assay for use in a full-scale, high-throughput screen.
Definition
The Z-factor is defined in terms of four parameters: the meanExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s and standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
s of both the positive (p) and negative (n) controls (
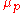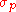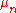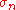, , and , ). Given these values, the Z-factor is defined as:In practice, the Z-factor is estimated from the sample mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
s and sample standard deviations
Interpretation
The following interpretations for the Z-factor are taken from :| Z-factor | Interpretation |
|---|---|
| 1.0 | Ideal. Z-factors can never exceed 1. |
| between 0.5 and 1.0 | An excellent assay. Note that if  , 0.5 is equivalent to a separation of 12 standard deviations between  and  . |
| between 0 and 0.5 | A marginal assay. |
| less than 0 | There is too much overlap between the positive and negative controls for the assay to be useful. |
Note that by the standards of many types of experiments, a zero Z-factor would suggest a large effect size, rather than a borderline useless result as suggested above. For example, if σp=σn=1, then μp=6 and μn=0 gives a zero Z-factor. But for normally-distributed data with these parameters, the probability that the positive control value would be less than the negative control value is less than 1 in 105. Extreme conservatism is used in high throughput screening due to the large number of tests performed.
Limitations
The constant factor 3 in the definition of the Z-factor is motivated by the normal distribution, for which more than 99% of values occur within 3 standard deviations of the mean. If the data follow a strongly non-normal distribution, the reference points (e.g. the meaning of a negative value) may be misleading. Another issue is that the usual estimates of the mean and standard deviation are not robustRobust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
. Extreme values (outliers) in either the positive or negative controls can adversely affect the Z-factor, potentially leading to an apparently favorable Z-factor even when there are severe problems with the assay
.
In addition, the application of the single Z-factor-based criterion to two or more positive controls with different strengths in the same assay will lead to misleading results
. The absolute sign in the Z-factor makes it inconvenient to derive the statistical inference of Z-factor mathematically
. A recently proposed statistical parameter, strictly standardized mean difference (SSMD), can address these issues
. One estimate of SSMD is robust to outliers.
Further reading
- Kraybill, B. (2005) "Quantitative Assay Evaluation and Optimization" (unpublished note)
- Zhang XHD (2011) "Optimal High-Throughput Screening: Practical Experimental Design and Data Analysis for Genome-scale RNAi Research, Cambridge University Press"