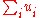Zero-sum
Encyclopedia
In game theory
and economic theory, a zero-sum game is a mathematical representation
of a situation in which a participant's gain (or loss) of utility
is exactly balanced by the losses (or gains) of the utility of other participant(s). If the total gains of the participants are added up, and the total losses are subtracted, they will sum to zero. Thus cutting a cake, where taking a larger piece reduces the amount of cake available for others, is a zero-sum game if all participants value each unit of cake equally (see marginal utility
). In contrast, non-zero-sum describes a situation in which the interacting parties' aggregate gains and losses are either less than or more than zero. A zero-sum game is also called a strictly competitive game. Zero-sum games are most often solved with the minimax theorem which is closely related to linear programming duality, or with Nash equilibrium
.
Situations where participants can all gain or suffer together are referred to as non-zero-sum. Thus, a country with an excess of bananas trading with another country for their excess of apples, where both benefit from the transaction, is in a non-zero-sum situation. Other non-zero-sum games are games in which the sum of gains and losses by the players are sometimes more or less than what they began with.
solution concept
s of Nash equilibrium
, minimax
, and maximin all give the same solution. In the solution, players play a mixed strategy.
A game's payoff matrix is a convenient representation. Consider for example the two-player zero-sum game pictured at right.
The order of play proceeds as follows: The first player (red) chooses in secret one of the two actions 1 or 2; the second player (blue), unaware of the first player's choice, chooses in secret one of the three actions A, B or C. Then, the choices are revealed and each player's points total is affected according to the payoff for those choices.
Example: Red chooses action 2 and Blue chooses action B. When the payoff is allocated, Red gains 20 points and Blue loses 20 points.
Now, in this example game both players know the payoff matrix and attempt to maximize the number of their points. What should they do?
Red could reason as follows: "With action 2, I could lose up to 20 points and can win only 20, while with action 1 I can lose only 10 but can win up to 30, so action 1 looks a lot better." With similar reasoning, Blue would choose action C. If both players take these actions, Red will win 20 points. But what happens if Blue anticipates Red's reasoning and choice of action 1, and goes for action B, so as to win 10 points? Or if Red in turn anticipates this devious trick and goes for action 2, so as to win 20 points after all?
Émile Borel
and John von Neumann
had the fundamental and surprising insight that probability
provides a way out of this conundrum. Instead of deciding on a definite action to take, the two players assign probabilities to their respective actions, and then use a random device which, according to these probabilities, chooses an action for them. Each player computes the probabilities so as to minimise the maximum expected
point-loss independent of the opponent's strategy. This leads to a linear programming
problem with the optimal strategies for each player. This minimax
method can compute provably optimal strategies for all two-player zero-sum games.
For the example given above, it turns out that Red should choose action 1 with probability 4/7 and action 2 with probability 3/7, while Blue should assign the probabilities 0, 4/7, and 3/7 to the three actions A, B, and C. Red will then win 20/7 points on average per game.
for a two-player, zero-sum game can be found by solving a linear programming
problem. Suppose a zero-sum game has a payoff matrix
where element 
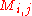is the payoff obtained when the minimizing player chooses pure strategy 
and the maximizing player chooses pure strategy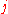 
(i.e. the player trying to minimize the payoff chooses the row and the player trying to maximize the payoff chooses the column). Assume every element of 
is positive. The game will have at least one Nash equilibrium. The Nash equilibrium can be found (see ref. [2], page 740) by solving the following linear program to find a vector 
:
The first constraint says each element of the
vector must be nonnegative, and the second constraint says each element of the 
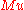vector must be at least 1. For the resulting 
vector, the inverse of the sum of its elements is the value of the game. Multiplying 
by that value gives a probability vector, giving the probability that the maximizing player will choose each of the possible pure strategies.
If the game matrix does not have all positive elements, simply add a constant to every element that is large enough to make them all positive. That will increase the value of the game by that constant, and will have no effect on the equilibrium mixed strategies for the equilibrium.
The equilibrium mixed strategy for the minimizing player can be found by solving the dual of the given linear program. Or, it can be found by using the above procedure to solve a modified payoff matrix which is the transpose and negation of
(adding a constant so it's positive), then solving the resulting game.
If all the solutions to the linear program are found, they will constitute all the Nash equilibria for the game. Conversely, any linear program can be converted into a two-player, zero-sum game by using a change of variables that puts it in the form of the above equations. So such games are equivalent to linear programs, in general.
, any commercial exchange is a non-zero-sum activity, because each party must consider the goods it is receiving as being at least fractionally more valuable than the goods it is delivering. Economic exchanges must benefit both parties enough above the zero-sum such that each party can overcome its transaction costs.
See also:
is the concept of "Social Traps". In some cases we can enhance our collective well-being by pursuing our personal interests — or parties can pursue mutually destructive behavior as they choose their own ends.
in his book Nonzero: The Logic of Human Destiny
, that society becomes increasingly non-zero-sum as it becomes more complex, specialized, and interdependent. As former US President
Bill Clinton
states:
and Oskar Morgenstern
proved that any zero-sum game involving n players is in fact a generalized form of a zero-sum game for two players, and that any non-zero-sum game for n players can be reduced to a zero-sum game for n + 1 players; the (n + 1) player representing the global profit or loss.
of the players, as well as to the interpretation of utility functions. Furthermore, the word "game" does not imply the model is valid only for recreational games
.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
and economic theory, a zero-sum game is a mathematical representation
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
of a situation in which a participant's gain (or loss) of utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
is exactly balanced by the losses (or gains) of the utility of other participant(s). If the total gains of the participants are added up, and the total losses are subtracted, they will sum to zero. Thus cutting a cake, where taking a larger piece reduces the amount of cake available for others, is a zero-sum game if all participants value each unit of cake equally (see marginal utility
Marginal utility
In economics, the marginal utility of a good or service is the utility gained from an increase in the consumption of that good or service...
). In contrast, non-zero-sum describes a situation in which the interacting parties' aggregate gains and losses are either less than or more than zero. A zero-sum game is also called a strictly competitive game. Zero-sum games are most often solved with the minimax theorem which is closely related to linear programming duality, or with Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
.
Definition
The zero-sum property (if one gains, another loses) means that any result of a zero-sum situation is Pareto optimal (generally, any game where all strategies are Pareto optimal is called a conflict game).Situations where participants can all gain or suffer together are referred to as non-zero-sum. Thus, a country with an excess of bananas trading with another country for their excess of apples, where both benefit from the transaction, is in a non-zero-sum situation. Other non-zero-sum games are games in which the sum of gains and losses by the players are sometimes more or less than what they began with.
Solution
For 2-player finite zero-sum games, the different game theoreticGame theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
solution concept
Solution concept
In game theory, a solution concept is a formal rule for predicting how the game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players, therefore predicting the result of the game...
s of Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
, minimax
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
, and maximin all give the same solution. In the solution, players play a mixed strategy.
Example
| A | B | C | |
|---|---|---|---|
| 1 | 30, -30 | -10, 10 | 20, -20 |
| 2 | 10, -10 | 20, -20 | -20, 20 |
A game's payoff matrix is a convenient representation. Consider for example the two-player zero-sum game pictured at right.
The order of play proceeds as follows: The first player (red) chooses in secret one of the two actions 1 or 2; the second player (blue), unaware of the first player's choice, chooses in secret one of the three actions A, B or C. Then, the choices are revealed and each player's points total is affected according to the payoff for those choices.
Example: Red chooses action 2 and Blue chooses action B. When the payoff is allocated, Red gains 20 points and Blue loses 20 points.
Now, in this example game both players know the payoff matrix and attempt to maximize the number of their points. What should they do?
Red could reason as follows: "With action 2, I could lose up to 20 points and can win only 20, while with action 1 I can lose only 10 but can win up to 30, so action 1 looks a lot better." With similar reasoning, Blue would choose action C. If both players take these actions, Red will win 20 points. But what happens if Blue anticipates Red's reasoning and choice of action 1, and goes for action B, so as to win 10 points? Or if Red in turn anticipates this devious trick and goes for action 2, so as to win 20 points after all?
Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
and John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
had the fundamental and surprising insight that probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
provides a way out of this conundrum. Instead of deciding on a definite action to take, the two players assign probabilities to their respective actions, and then use a random device which, according to these probabilities, chooses an action for them. Each player computes the probabilities so as to minimise the maximum expected
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
point-loss independent of the opponent's strategy. This leads to a linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problem with the optimal strategies for each player. This minimax
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
method can compute provably optimal strategies for all two-player zero-sum games.
For the example given above, it turns out that Red should choose action 1 with probability 4/7 and action 2 with probability 3/7, while Blue should assign the probabilities 0, 4/7, and 3/7 to the three actions A, B, and C. Red will then win 20/7 points on average per game.
Solving
The Nash equilibriumNash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
for a two-player, zero-sum game can be found by solving a linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problem. Suppose a zero-sum game has a payoff matrix
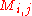where element is the payoff obtained when the minimizing player chooses pure strategy 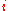and the maximizing player chooses pure strategy 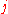(i.e. the player trying to minimize the payoff chooses the row and the player trying to maximize the payoff chooses the column). Assume every element of is positive. The game will have at least one Nash equilibrium. The Nash equilibrium can be found (see ref. [2], page 740) by solving the following linear program to find a vector :- Minimize:
-
- Subject to the constraints:
≥ 0
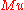≥ 1.
The first constraint says each element of the
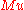vector must be nonnegative, and the second constraint says each element of the vector must be at least 1. For the resulting vector, the inverse of the sum of its elements is the value of the game. Multiplying by that value gives a probability vector, giving the probability that the maximizing player will choose each of the possible pure strategies.If the game matrix does not have all positive elements, simply add a constant to every element that is large enough to make them all positive. That will increase the value of the game by that constant, and will have no effect on the equilibrium mixed strategies for the equilibrium.
The equilibrium mixed strategy for the minimizing player can be found by solving the dual of the given linear program. Or, it can be found by using the above procedure to solve a modified payoff matrix which is the transpose and negation of
(adding a constant so it's positive), then solving the resulting game.If all the solutions to the linear program are found, they will constitute all the Nash equilibria for the game. Conversely, any linear program can be converted into a two-player, zero-sum game by using a change of variables that puts it in the form of the above equations. So such games are equivalent to linear programs, in general.
Economics
Many economic situations are not zero-sum, since valuable goods and services can be created, destroyed, or badly allocated, and any of these will create a net gain or loss. Assuming the counterparties are acting rationally with symmetric informationInformation asymmetry
In economics and contract theory, information asymmetry deals with the study of decisions in transactions where one party has more or better information than the other. This creates an imbalance of power in transactions which can sometimes cause the transactions to go awry, a kind of market failure...
, any commercial exchange is a non-zero-sum activity, because each party must consider the goods it is receiving as being at least fractionally more valuable than the goods it is delivering. Economic exchanges must benefit both parties enough above the zero-sum such that each party can overcome its transaction costs.
See also:
- Comparative advantageComparative advantageIn economics, the law of comparative advantage says that two countries will both gain from trade if, in the absence of trade, they have different relative costs for producing the same goods...
- Zero-sum fallacy
- Gains from tradeGains from tradeGains from trade in economics refers to net benefits to agents from allowing an increase in voluntary trading with each other. In technical terms, it is the increase of consumer surplus plus producer surplus from lower tariffs or otherwise liberalizing trade...
- Free tradeFree tradeUnder a free trade policy, prices emerge from supply and demand, and are the sole determinant of resource allocation. 'Free' trade differs from other forms of trade policy where the allocation of goods and services among trading countries are determined by price strategies that may differ from...
Psychology
The most common or simple example from the subfield of Social PsychologySocial psychology
Social psychology is the scientific study of how people's thoughts, feelings, and behaviors are influenced by the actual, imagined, or implied presence of others. By this definition, scientific refers to the empirical method of investigation. The terms thoughts, feelings, and behaviors include all...
is the concept of "Social Traps". In some cases we can enhance our collective well-being by pursuing our personal interests — or parties can pursue mutually destructive behavior as they choose their own ends.
Complexity
It has been theorized by Robert WrightRobert Wright (journalist)
Robert Wright is an American journalist, scholar, and prize-winning author of best-selling books about science, evolutionary psychology, history, religion, and game theory, including The Evolution of God, Nonzero: The Logic of Human Destiny, The Moral Animal, and Three Scientists and Their Gods:...
in his book Nonzero: The Logic of Human Destiny
Nonzero: The Logic of Human Destiny
Nonzero: The Logic of Human Destiny is a book by Robert Wright originally published in 2000. It argues that biological evolution and cultural evolution are shaped and directed first and foremost by "non-zero-sumness," that is, the prospect of creating new interactions that are not zero-sum.- Thesis...
, that society becomes increasingly non-zero-sum as it becomes more complex, specialized, and interdependent. As former US President
President of the United States
The President of the United States of America is the head of state and head of government of the United States. The president leads the executive branch of the federal government and is the commander-in-chief of the United States Armed Forces....
Bill Clinton
Bill Clinton
William Jefferson "Bill" Clinton is an American politician who served as the 42nd President of the United States from 1993 to 2001. Inaugurated at age 46, he was the third-youngest president. He took office at the end of the Cold War, and was the first president of the baby boomer generation...
states:
Extensions
In 1944 John von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
and Oskar Morgenstern
Oskar Morgenstern
Oskar Morgenstern was a German-born Austrian-School economist. He, along with John von Neumann, helped found the mathematical field of game theory ....
proved that any zero-sum game involving n players is in fact a generalized form of a zero-sum game for two players, and that any non-zero-sum game for n players can be reduced to a zero-sum game for n + 1 players; the (n + 1) player representing the global profit or loss.
Misunderstandings
Zero–sum games and particularly their solutions are commonly misunderstood by critics of game theory, usually with respect to the independence and rationalityRational choice theory
Rational choice theory, also known as choice theory or rational action theory, is a framework for understanding and often formally modeling social and economic behavior. It is the main theoretical paradigm in the currently-dominant school of microeconomics...
of the players, as well as to the interpretation of utility functions. Furthermore, the word "game" does not imply the model is valid only for recreational games
Games
The term games is the plural of gameIt may refer to:* GamesTM magazine* Games * Games, an electronic music album by Larry Fast* Games , an album by Leo Ku* Games * "Games" , an episode of the TV series House...
.
External links
- Play zero-sum games online by Elmer G. Wiens.
- Game Theory & its Applications - comprehensive text on psychology and game theory. (Contents and Preface to Second Edition.)