Zipf's law
Encyclopedia
Zipf's law an empirical law formulated using mathematical statistics
, refers to the fact that many types of data studied in the physical
and social sciences can be approximated with a Zipfian distribution, one of a family of related discrete power law
probability distribution
s. The law is named after the linguist
George Kingsley Zipf who first proposed it (Zipf 1935, 1949), though Jean-Baptiste Estoup
appears to have noticed the regularity before Zipf.
of natural language
utterances, the frequency of any word is inversely proportional to its rank in the frequency table. Thus the most frequent word will occur approximately twice as often as the second most frequent word, three times as often as the third most frequent word, etc. For example, in the Brown Corpus
"the" is the most frequently occurring word, and by itself accounts for nearly 7% of all word occurrences (69,971 out of slightly over 1 million). True to Zipf's Law, the second-place word "of" accounts for slightly over 3.5% of words (36,411 occurrences), followed by "and" (28,852). Only 135 vocabulary items are needed to account for half the Brown Corpus.
The same relationship occurs in many other rankings, unrelated to language, such as the population ranks of cities in various countries, corporation sizes, income rankings, etc. The appearance of the distribution in rankings of cities by population was first noticed by Felix Auerbach in 1913. Empirically a data set can be tested to see if Zipf's law applies by running the regression log R = a - b log n where R is the rank of the datum, n is its value and a and b are constants. For Zipf's law applies when b = 1. When this regression is applied to cities a better fit has been found with b = 1.07. While Zipf's law holds for the upper tail of the distribution, the entire distribution of cities is lognormal and follows Gibrat's law
. Both laws are consistent because a lognormal tail can typically not be distinguished from a Pareto (Zipf) tail.
the data on a log-log graph, with the axes being log
(rank order) and log (frequency). For example, the word "the" (as described above) would appear at x = log(1), y = log(69971). The data conform to Zipf's law to the extent that the plot is linear
.
Formally, let:
Zipf's law then predicts that out of a population of N elements, the frequency of elements of rank k, f(k;s,N), is:
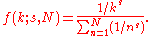
Zipf's law holds if the number of occurrences of each element are independent and identically distributed random variables with power law distribution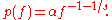
In the example of the frequency of words in the English language, N is the number of words in the English language and, if we use the classic version of Zipf's law, the exponent s is 1. f(k; s,N) will then be the fraction of the time the kth most common word occurs.
The law may also be written:
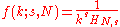
where HN,s is the Nth generalized harmonic number.
The simplest case of Zipf's law is a "1⁄f function". Given a set of Zipfian distributed frequencies, sorted from most common to least common, the second most common frequency will occur ½ as often as the first. The third most common frequency will occur ⅓ as often as the first. The nth most common frequency will occur 1⁄n as often as the first. However, this cannot hold exactly, because items must occur an integer number of times; there cannot be 2.5 occurrences of a word. Nevertheless, over fairly wide ranges, and to a fairly good approximation, many natural phenomena obey Zipf's law.
Mathematically, the sum of all relative frequencies in a Zipf distribution is equal to the harmonic series
and therefore:
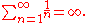
In human languages, word frequencies have a very heavy-tailed distribution, and can therefore be modeled reasonably well by a Zipf distribution with an s close to 1.
As long as the exponent s exceeds 1, it is possible for such a law to hold with infinitely many words, since if s > 1 then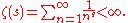
where ζ is Riemann's zeta function.
in a paper, On the Statistical Laws of Linguistic Distribution offered a mathematical derivation. He took a large class of well-behaved statistical distributions (not only the normal distribution) and expressed them in terms of rank. He then expanded each expression into a Taylor series
. In every case Belevitch obtained the remarkable result that a first-order truncation of the series resulted in Zipf's law. Further, a second-order truncation of the Taylor series resulted in Mandelbrot's law.
Zipf himself proposed that neither speakers nor hearers using a given language want to work any harder than necessary to reach understanding, and the process that results in approximately equal distribution of effort leads to the observed Zipf distribution.
 Zipf's law now refers more generally to frequency distributions of "rank data," in which the relative frequency of the nth-ranked item is given by the Zeta distribution, 1/(nsζ(s)), where the parameter s > 1 indexes the members of this family of probability distribution
Zipf's law now refers more generally to frequency distributions of "rank data," in which the relative frequency of the nth-ranked item is given by the Zeta distribution, 1/(nsζ(s)), where the parameter s > 1 indexes the members of this family of probability distribution
s. Indeed, Zipf's law is sometimes synonymous with "zeta distribution," since probability distributions are sometimes called "laws". This distribution is sometimes called the Zipfian or Yule distribution.
A generalization of Zipf's law is the Zipf–Mandelbrot law, proposed by Benoît Mandelbrot
, whose frequencies are:

The "constant" is the reciprocal of the Hurwitz zeta function evaluated at s.
Zipfian distributions can be obtained from Pareto distributions by an exchange of variables.
The tail frequencies of the Yule–Simon distribution are approximately

for any choice of ρ > 0.
In the parabolic fractal distribution
, the logarithm of the frequency is a quadratic polynomial of the logarithm of the rank. This can markedly improve the fit over a simple power-law relationship. Like fractal dimension, it is possible to calculate Zipf dimension, which is a useful parameter in the analysis of texts.
It has been argued that Benford's law
is a special bounded case of Zipf's law, with the connection between these two laws being explained by their both originating from scale invariant functional relations from statistical physics and critical phenomena. The ratios of probabilities in Benford's law are not constant.
Secondary:
Mathematical statistics
Mathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
, refers to the fact that many types of data studied in the physical
Physical science
Physical science is an encompassing term for the branches of natural science and science that study non-living systems, in contrast to the life sciences...
and social sciences can be approximated with a Zipfian distribution, one of a family of related discrete power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s. The law is named after the linguist
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
George Kingsley Zipf who first proposed it (Zipf 1935, 1949), though Jean-Baptiste Estoup
Jean-Baptiste Estoup
Jean-Baptiste Estoup was a French stenographer and writer on stenography.Estoup was General Secretary of the Institut Sténographique de France. In his Gammes sténographiques , he pioneered the investigation of the regularity later known as Zipf's law.-References:...
appears to have noticed the regularity before Zipf.
Motivation
Zipf's law states that given some corpusText corpus
In linguistics, a corpus or text corpus is a large and structured set of texts...
of natural language
Natural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
utterances, the frequency of any word is inversely proportional to its rank in the frequency table. Thus the most frequent word will occur approximately twice as often as the second most frequent word, three times as often as the third most frequent word, etc. For example, in the Brown Corpus
Brown Corpus
The Brown University Standard Corpus of Present-Day American English was compiled in the 1960s by Henry Kucera and W. Nelson Francis at Brown University, Providence, Rhode Island as a general corpus in the field of corpus linguistics...
"the" is the most frequently occurring word, and by itself accounts for nearly 7% of all word occurrences (69,971 out of slightly over 1 million). True to Zipf's Law, the second-place word "of" accounts for slightly over 3.5% of words (36,411 occurrences), followed by "and" (28,852). Only 135 vocabulary items are needed to account for half the Brown Corpus.
The same relationship occurs in many other rankings, unrelated to language, such as the population ranks of cities in various countries, corporation sizes, income rankings, etc. The appearance of the distribution in rankings of cities by population was first noticed by Felix Auerbach in 1913. Empirically a data set can be tested to see if Zipf's law applies by running the regression log R = a - b log n where R is the rank of the datum, n is its value and a and b are constants. For Zipf's law applies when b = 1. When this regression is applied to cities a better fit has been found with b = 1.07. While Zipf's law holds for the upper tail of the distribution, the entire distribution of cities is lognormal and follows Gibrat's law
Gibrat's law
Gibrat's law, sometimes called Gibrat's rule of proportionate growth is a rule defined by Robert Gibrat stating that the size of a firm and its growth rate are independent. The law proportionate growth gives rise to a distribution that is log-normal...
. Both laws are consistent because a lognormal tail can typically not be distinguished from a Pareto (Zipf) tail.
Theoretical review
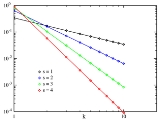
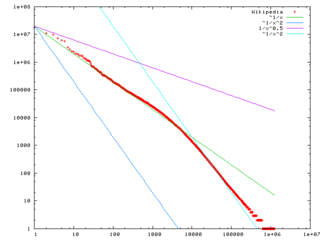
Zipf's law is most easily observed by plottingGraph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
the data on a log-log graph, with the axes being log
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
(rank order) and log (frequency). For example, the word "the" (as described above) would appear at x = log(1), y = log(69971). The data conform to Zipf's law to the extent that the plot is linear
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
.
Formally, let:
- N be the number of elements;
- k be their rank;
- s be the value of the exponent characterizing the distribution.
Zipf's law then predicts that out of a population of N elements, the frequency of elements of rank k, f(k;s,N), is:
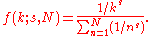
Zipf's law holds if the number of occurrences of each element are independent and identically distributed random variables with power law distribution
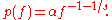
In the example of the frequency of words in the English language, N is the number of words in the English language and, if we use the classic version of Zipf's law, the exponent s is 1. f(k; s,N) will then be the fraction of the time the kth most common word occurs.
The law may also be written:
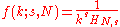
where HN,s is the Nth generalized harmonic number.
The simplest case of Zipf's law is a "1⁄f function". Given a set of Zipfian distributed frequencies, sorted from most common to least common, the second most common frequency will occur ½ as often as the first. The third most common frequency will occur ⅓ as often as the first. The nth most common frequency will occur 1⁄n as often as the first. However, this cannot hold exactly, because items must occur an integer number of times; there cannot be 2.5 occurrences of a word. Nevertheless, over fairly wide ranges, and to a fairly good approximation, many natural phenomena obey Zipf's law.
Mathematically, the sum of all relative frequencies in a Zipf distribution is equal to the harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
and therefore:
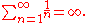
In human languages, word frequencies have a very heavy-tailed distribution, and can therefore be modeled reasonably well by a Zipf distribution with an s close to 1.
As long as the exponent s exceeds 1, it is possible for such a law to hold with infinitely many words, since if s > 1 then
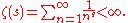
where ζ is Riemann's zeta function.
Statistical explanation
It is not known why Zipf's law holds for most languages. However, it may be partially explained by the statistical analysis of randomly-generated texts. Wentian Li has shown that in a document in which each character has been chosen randomly from a uniform distribution of all letters (plus a space character), the "words" follow the general trend of Zipf's law (appearing approximately linear on log-log plot). Vitold BelevitchVitold Belevitch
Vitold Belevitch was a Belgian mathematician and electrical engineer of Russian extraction who produced some important work in the field of electrical network theory. Born to parents fleeing the Bolsheviks, he settled in Belgium where he worked on early computer construction projects...
in a paper, On the Statistical Laws of Linguistic Distribution offered a mathematical derivation. He took a large class of well-behaved statistical distributions (not only the normal distribution) and expressed them in terms of rank. He then expanded each expression into a Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
. In every case Belevitch obtained the remarkable result that a first-order truncation of the series resulted in Zipf's law. Further, a second-order truncation of the Taylor series resulted in Mandelbrot's law.
Zipf himself proposed that neither speakers nor hearers using a given language want to work any harder than necessary to reach understanding, and the process that results in approximately equal distribution of effort leads to the observed Zipf distribution.
Related laws

Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s. Indeed, Zipf's law is sometimes synonymous with "zeta distribution," since probability distributions are sometimes called "laws". This distribution is sometimes called the Zipfian or Yule distribution.
A generalization of Zipf's law is the Zipf–Mandelbrot law, proposed by Benoît Mandelbrot
Benoît Mandelbrot
Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
, whose frequencies are:

The "constant" is the reciprocal of the Hurwitz zeta function evaluated at s.
Zipfian distributions can be obtained from Pareto distributions by an exchange of variables.
The tail frequencies of the Yule–Simon distribution are approximately

for any choice of ρ > 0.
In the parabolic fractal distribution
Parabolic fractal distribution
In probability and statistics, the parabolic fractal distribution is a type of discrete probability distribution in which the logarithm of the frequency or size of entities in a population is a quadratic polynomial of the logarithm of the rank...
, the logarithm of the frequency is a quadratic polynomial of the logarithm of the rank. This can markedly improve the fit over a simple power-law relationship. Like fractal dimension, it is possible to calculate Zipf dimension, which is a useful parameter in the analysis of texts.
It has been argued that Benford's law
Benford's law
Benford's law, also called the first-digit law, states that in lists of numbers from many real-life sources of data, the leading digit is distributed in a specific, non-uniform way...
is a special bounded case of Zipf's law, with the connection between these two laws being explained by their both originating from scale invariant functional relations from statistical physics and critical phenomena. The ratios of probabilities in Benford's law are not constant.
 |
Benford's law: 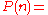  |
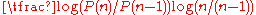 |
|---|---|---|
| 1 | 0.30103000 | |
| 2 | 0.17609126 | -0.7735840 |
| 3 | 0.12493874 | -0.8463832 |
| 4 | 0.09691001 | -0.8830605 |
| 5 | 0.07918125 | -0.9054412 |
| 6 | 0.06694679 | -0.9205788 |
| 7 | 0.05799195 | -0.9315169 |
| 8 | 0.05115252 | -0.9397966 |
| 9 | 0.04575749 | -0.9462848 |
See also
- Benford's lawBenford's lawBenford's law, also called the first-digit law, states that in lists of numbers from many real-life sources of data, the leading digit is distributed in a specific, non-uniform way...
- Bradford's lawBradford's lawBradford's law is a pattern first described by Samuel C. Bradford in 1934 that estimates the exponentially diminishing returns of extending a search for references in science journals...
- Demographic gravitationDemographic GravitationDemographic gravitation is a concept of "social physics", introduced by Princeton University astrophysicist John Quincy Stewart in 1947. It is an attempt to use equations and notions of classical physics - such as gravity - to seek simplified insights and even laws of demographic behaviour for...
- Frequency listFrequency listIn computational linguistics, a frequency list is a sorted list of words together with their frequency, where frequency here usually means the number of occurrences in a given corpus...
- Gibrat's lawGibrat's lawGibrat's law, sometimes called Gibrat's rule of proportionate growth is a rule defined by Robert Gibrat stating that the size of a firm and its growth rate are independent. The law proportionate growth gives rise to a distribution that is log-normal...
- Heaps' lawHeaps' lawIn linguistics, Heaps' law is an empirical law which describes the portion of a vocabulary which is represented by an instance document consisting of words chosen from the vocabulary. This can be formulated as V_R = Kn^\beta...
- Hapax legomenonHapax legomenonA hapax legomenon is a word which occurs only once within a context, either in the written record of an entire language, in the works of an author, or just in a single text. The term is sometimes used incorrectly to describe a word that occurs in just one of an author's works, even though it...
- Jean-Baptiste EstoupJean-Baptiste EstoupJean-Baptiste Estoup was a French stenographer and writer on stenography.Estoup was General Secretary of the Institut Sténographique de France. In his Gammes sténographiques , he pioneered the investigation of the regularity later known as Zipf's law.-References:...
- Lorenz curveLorenz curveIn economics, the Lorenz curve is a graphical representation of the cumulative distribution function of the empirical probability distribution of wealth; it is a graph showing the proportion of the distribution assumed by the bottom y% of the values...
- Lotka's law
- Moore's lawMoore's LawMoore's law describes a long-term trend in the history of computing hardware: the number of transistors that can be placed inexpensively on an integrated circuit doubles approximately every two years....
- Pareto distribution
- Pareto principlePareto principleThe Pareto principle states that, for many events, roughly 80% of the effects come from 20% of the causes.Business-management consultant Joseph M...
aka the "80-20 rule" - Power lawPower lawA power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
- Principle of least effortPrinciple of least effortThe principle of least effort is a broad theory that covers diverse fields from evolutionary biology to webpage design. It postulates that animals, people, even well designed machines will naturally choose the path of least resistance or "effort". It is closely related to many other similar...
- Rank-size distributionRank-size distributionRank-size distribution or the rank-size rule describes the remarkable regularity in many phenomena including the distribution of city sizes around the world, sizes of businesses, particle sizes , lengths of rivers, frequencies of word usage, wealth among individuals, etc...
- Zipf–Mandelbrot law
Further reading
Primary:- George K. Zipf (1949) Human Behavior and the Principle of Least Effort. Addison-Wesley.
- George K. Zipf (1935) The Psychobiology of Language. Houghton-Mifflin. (see citations at http://citeseer.ist.psu.edu/context/64879/0 )
Secondary:
- Gelbukh, Alexander, and Sidorov, Grigori (2001) "Zipf and Heaps Laws’ Coefficients Depend on Language". Proc. CICLing-2001, Conference on Intelligent Text Processing and Computational Linguistics, February 18–24, 2001, Mexico City. Lecture Notes in Computer Science N 2004, ISSN 0302-9743, ISBN 3-540-41687-0, Springer-Verlag: 332–335.
- Damián H. Zanette (2006) "Zipf's law and the creation of musical context," Musicae Scientiae 10: 3-18.
- Kali R. (2003) "The city as a giant component: a random graph approach to Zipf's law," Applied Economics Letters 10: 717-720(4)
External links
-- An article on Zipf's law applied to city populations- Comprehensive bibliography of Zipf's law
- Seeing Around Corners (Artificial societies turn up Zipf's law)
- PlanetMath article on Zipf's law
- Distributions de type “fractal parabolique” dans la Nature (French, with English summary)
- An analysis of income distribution
- Zipf List of French words
- Zipf list for English, French, Spanish, Italian, Swedish, Icelandic, Latin, Portugese and Finnish from Gutenberg Project and online calculator to rank words in texts
- Citations and the Zipf-Mandelbrot's law
- Zipf's Law for U.S. Cities by Fiona Maclachlan, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Zipf's Law examples and modelling (1985)
- Complex systems: Unzipping Zipf's law (2011)

