Zeta distribution
Encyclopedia
In probability theory
and statistics
, the zeta distribution is a discrete probability distribution
. If X is a zeta-distributed random variable
with parameter s, then the probability that X takes the integer value k is given by the probability mass function
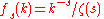
where ζ(s) is the Riemann zeta function (which is undefined for s = 1).
The multiplicities of distinct prime factor
s of X are independent
random variable
s.
The zeta distribution is equivalent to the Zipf distribution for infinite N. Indeed the terms "Zipf distribution" and the "zeta distribution" are often used interchangeably.
is defined as the expected value of Xn:
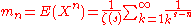
The series on the right is just a series representation of the Riemann zeta function, but it only converges for values of s-n that are greater than unity. Thus:
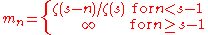
Note that the ratio of the zeta functions is well defined, even for n ≥ s − 1 because the series representation of the zeta function can be analytically continued
. This does not change the fact that the moments are specified by the series itself, and are therefore undefined for large n.
The series is just the definition of the polylogarithm, valid for
so that
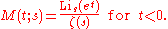
The Taylor series
expansion of this function will not necessarily yield the moments of the distribution. The Taylor series using the moments as they usually occur in the moment generating function yields
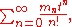
which obviously is not well defined for any finite value of s since the moments become infinite for large n. If we use the analytically continued terms instead of the moments themselves, we obtain from a series representation of the polylogarithm
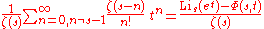
for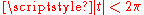
. 
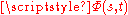is given by
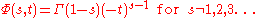
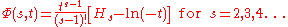
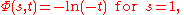
where Hs is a harmonic number.
, and so the case when s = 1 is not meaningful. However, if A is any set of positive integers that has a density, i.e. if
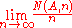
exists where N(A, n) is the number of members of A less than or equal to n, then
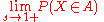
is equal to that density.
The latter limit can also exist in some cases in which A does not have a density. For example, if A is the set of all positive integers whose first digit is d, then A has no density, but nonetheless the second limit given above exists and is proportional to
similar to Benford's law
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the zeta distribution is a discrete probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. If X is a zeta-distributed random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with parameter s, then the probability that X takes the integer value k is given by the probability mass function
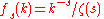
where ζ(s) is the Riemann zeta function (which is undefined for s = 1).
The multiplicities of distinct prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s of X are independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s.
The zeta distribution is equivalent to the Zipf distribution for infinite N. Indeed the terms "Zipf distribution" and the "zeta distribution" are often used interchangeably.
Moments
The nth raw momentMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
is defined as the expected value of Xn:
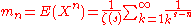
The series on the right is just a series representation of the Riemann zeta function, but it only converges for values of s-n that are greater than unity. Thus:
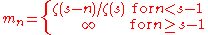
Note that the ratio of the zeta functions is well defined, even for n ≥ s − 1 because the series representation of the zeta function can be analytically continued
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
. This does not change the fact that the moments are specified by the series itself, and are therefore undefined for large n.
Moment generating function
The moment generating function is defined asThe series is just the definition of the polylogarithm, valid for
so that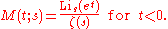The Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion of this function will not necessarily yield the moments of the distribution. The Taylor series using the moments as they usually occur in the moment generating function yields
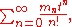
which obviously is not well defined for any finite value of s since the moments become infinite for large n. If we use the analytically continued terms instead of the moments themselves, we obtain from a series representation of the polylogarithm
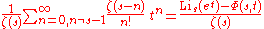
for
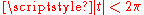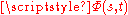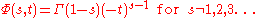
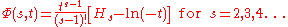
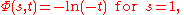
. is given bywhere Hs is a harmonic number.
The case s = 1
ζ(1) is infinite as the harmonic seriesHarmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
, and so the case when s = 1 is not meaningful. However, if A is any set of positive integers that has a density, i.e. if
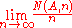
exists where N(A, n) is the number of members of A less than or equal to n, then
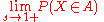
is equal to that density.
The latter limit can also exist in some cases in which A does not have a density. For example, if A is the set of all positive integers whose first digit is d, then A has no density, but nonetheless the second limit given above exists and is proportional to
similar to Benford's law
Benford's law
Benford's law, also called the first-digit law, states that in lists of numbers from many real-life sources of data, the leading digit is distributed in a specific, non-uniform way...
.
See also
Other "power-law" distributions- Cauchy distributionCauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
- Lévy distribution
- Lévy skew alpha-stable distribution
- Pareto distribution
- Zipf's law
- Zipf–Mandelbrot law
External links
- Some remarks on the Riemann zeta distribution by Allan Gut. What Gut calls the Riemann zeta distribution is actually the probability distribution of −log X, where X is a random variable with what this article calls the zeta distribution.