Levy skew alpha-stable distribution
Encyclopedia
In probability theory
, a random variable
is said to be stable (or to have a stable distribution) if it has the property that a linear combination of two independent copies of the variable has the same distribution
, up to
location
and scale
parameters. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution.
The importance of stable probability distributions is that they are "attractors" for properly normed sums of independent and identically-distributed (iid) random variables. The normal distribution is one family of stable distributions. By the classical central limit theorem
the properly normed sum of a set of random variables, each with finite variance, will tend towards a normal distribution as the number of variables increases. Without the finite variance assumption the limit may be a stable distribution. Stable distributions that are non-normal are often called stable Paretian distributions, after Vilfredo Pareto
.
Umarov, Tsallis, Gell-Mann and Steinberg have defined q-analog
s of all symmetric stable distributions which recover the usual symmetric stable distributions in the limit of q->1.
Since the normal distribution, the Cauchy distribution
, and the Lévy distribution all have the above property, it follows that they are special cases of stable distributions.
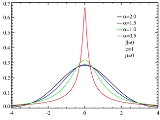
Such distributions form a four-parameter family of continuous probability distribution
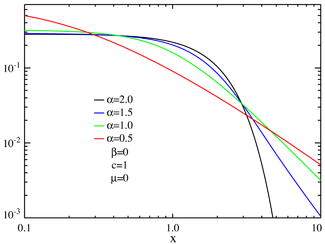
s parametrized by location and scale parameters μ and c, respectively, and two shape parameters β and α, roughly corresponding to measures of asymmetry and concentration, respectively (see the figures).
Although the probability density function for a general stable distribution cannot be written analytically, the general characteristic function can be. Any probability distribution is determined by its characteristic function
 by:
by:
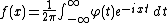
A random variable X is called stable if its characteristic function is given by (see and )
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is said to be stable (or to have a stable distribution) if it has the property that a linear combination of two independent copies of the variable has the same distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
location
Location parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
and scale
Scale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
parameters. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution.
The importance of stable probability distributions is that they are "attractors" for properly normed sums of independent and identically-distributed (iid) random variables. The normal distribution is one family of stable distributions. By the classical central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
the properly normed sum of a set of random variables, each with finite variance, will tend towards a normal distribution as the number of variables increases. Without the finite variance assumption the limit may be a stable distribution. Stable distributions that are non-normal are often called stable Paretian distributions, after Vilfredo Pareto
Vilfredo Pareto
Vilfredo Federico Damaso Pareto , born Wilfried Fritz Pareto, was an Italian engineer, sociologist, economist, political scientist and philosopher. He made several important contributions to economics, particularly in the study of income distribution and in the analysis of individuals' choices....
.
Umarov, Tsallis, Gell-Mann and Steinberg have defined q-analog
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
s of all symmetric stable distributions which recover the usual symmetric stable distributions in the limit of q->1.
Definition
A non-degenerate distribution is a stable distribution if it satisfies the following property:- Let X1 and X2 be independent copies of a random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X. Random variable X is said to be stable if for any constants a and b the random variable aX1 + bX2 has the same distribution as cX + d with some constants c and d. The distribution is said to be strictly stable if this holds with d = 0 .
Since the normal distribution, the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
, and the Lévy distribution all have the above property, it follows that they are special cases of stable distributions.
Such distributions form a four-parameter family of continuous probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s parametrized by location and scale parameters μ and c, respectively, and two shape parameters β and α, roughly corresponding to measures of asymmetry and concentration, respectively (see the figures).
Although the probability density function for a general stable distribution cannot be written analytically, the general characteristic function can be. Any probability distribution is determined by its characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
 by:
by: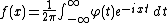
A random variable X is called stable if its characteristic function is given by (see and )
-
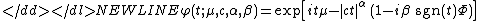
where sgn(t) is just the signSign functionIn mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
of t and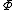 is given by
is given by

for all except
except 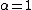 in which case:
in which case:
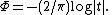
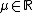 is a shift parameter,
is a shift parameter, 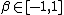 , called the skewness parameter, is a measure of asymmetry. Notice that in this context the usual skewnessSkewnessIn probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
, called the skewness parameter, is a measure of asymmetry. Notice that in this context the usual skewnessSkewnessIn probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
is not well defined, as for α<2 the distribution does not admit 2nd or higher momentsMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
, and the usual skewness definition is the 3rd central momentCentral momentIn probability theory and statistics, central moments form one set of values by which the properties of a probability distribution can be usefully characterised...
.
In the simplest case β = 0, the characteristic function is just a stretched exponential function; the distribution is symmetric about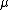 and is referred to as a (Lévy) symmetric alpha-stable distribution.
and is referred to as a (Lévy) symmetric alpha-stable distribution.
When α<1, β=1 and μ=0, the distribution is supported by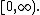
The parameter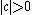 is a scale factor which is a measure of the width of the distribution and
is a scale factor which is a measure of the width of the distribution and  is the exponent or index of the distribution and specifies the asymptotic behavior of the distribution for α < 2.
is the exponent or index of the distribution and specifies the asymptotic behavior of the distribution for α < 2.
Parameterizations
The above definition is only one of the parameterizations in use for stable distributions; it is the most common but is not continuous in the parameters. For example, for the case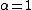 we could replace
we could replace 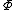 by:
by:
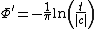
and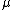 by
by
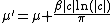
This parameterization has the advantage that we may define a standard distribution using
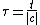
and
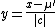
The pdf for all will then have the following standardization property:
will then have the following standardization property:
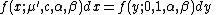
Applications
Stable distributions owe their importance in both theory and practice to the generalization of the central limit theoremCentral limit theoremIn probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
to random variables without second (and possibly first) order momentsMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
and the accompanying self-similaritySelf-similarityIn mathematics, a self-similar object is exactly or approximately similar to a part of itself . Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales...
of the stable family. It was the seeming departure from normality along with the demand for a self-similar model for financial data (i.e. the shape of the distribution for yearly asset price changes should resemble that of the constituent daily or monthly price changes) that led Benoît MandelbrotBenoît MandelbrotBenoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
to propose that cotton prices follow an alpha-stable distribution with α equal to 1.7. Lévy distributions are frequently found in analysis of critical behavior and financial data .
They are also found in spectroscopySpectroscopySpectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
as a general expression for a quasistatically pressure-broadened spectral lineSpectral lineA spectral line is a dark or bright line in an otherwise uniform and continuous spectrum, resulting from a deficiency or excess of photons in a narrow frequency range, compared with the nearby frequencies.- Types of line spectra :...
.
The statistics of solar flares are described by a non-Gaussian distribution. The solar flare statistics were shown to be describable by a Lévy distribution and it was assumed that intermittent solar flares perturb the intrinsic fluctuations in Earth’s average temperature. The end result of this perturbation is that the statistics of the temperature anomalies inherit the statistical structure that was evident in the intermittency of the solar flare data.
Lévy distribution of solar flare waiting time events (time between flare events) was demonstrated for CGRO BATSE hard x-ray solar flares December 2001. Analysis of the Lévy statistical signature revealed that two different memory signatures were evident; one related to the solar cycle and the second whose origin appears to be associated with a localized or combination of localized solar active region effects.
Properties
- All stable distributions are infinitely divisible.
- With the exception of the normal distribution (α = 2), stable distributions are leptokurtotic and heavy-tailed distributionHeavy-tailed distributionIn probability theory, heavy-tailed distributions are probability distributions whose tails are not exponentially bounded: that is, they have heavier tails than the exponential distribution...
s. - Closure under convolution
Stable distributions are closed under convolution for a fixed value of . Since convolution is equivalent to multiplication of the Fourier-transformed function, it follows that the product of two stable characteristic functions with the same
. Since convolution is equivalent to multiplication of the Fourier-transformed function, it follows that the product of two stable characteristic functions with the same  will yield another such characteristic function. The product of two stable characteristic functions is given by:
will yield another such characteristic function. The product of two stable characteristic functions is given by:
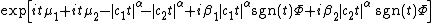
Since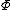 is not a function of the
is not a function of the 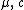 or
or 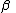 variables it follows that these parameters for the convolved function are given by:
variables it follows that these parameters for the convolved function are given by:
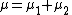
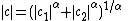

In each case, it can be shown that the resulting parameters lie within the required intervals for a stable distribution.
The distribution
A stable distribution is therefore specified by the above four parameters. It can be shown that any non-degenerate stable distribution has a smooth (infinitely differentiable) density function. If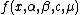 denotes the density of X and
denotes the density of X and
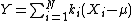 (sum of independent copies of X)
(sum of independent copies of X)
then Y has the density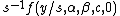 with
with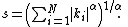
The asymptotic behavior is described, for α < 2, by:
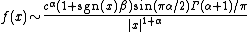
where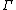 is the Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
is the Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
(except that when α < 1 and β = 1 or −1, the tail vanishes to the left or right, resp., of μ).
This "heavy tail" behavior causes the variance of stable distributions to be infinite for all . This property is illustrated in the log-log plots below.
. This property is illustrated in the log-log plots below.
When α=2, the distribution is Gaussian (see below), with tails asymptotic to exp(−x2/4c2)/(2c√π).
Special cases
 There is no general analytic solution for the form of p(x). There are, however three special cases which can be expressed in terms of elementary functions as can be seen by inspection of the characteristic function
There is no general analytic solution for the form of p(x). There are, however three special cases which can be expressed in terms of elementary functions as can be seen by inspection of the characteristic function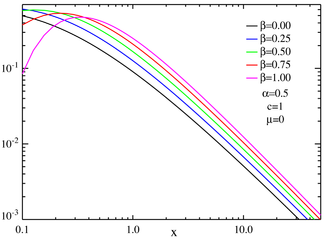 Characteristic function (probability theory)In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
Characteristic function (probability theory)In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
.
- For α = 2 the distribution reduces to a Gaussian distribution with variance
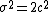 and mean
and mean  ; the skewness parameter
; the skewness parameter 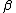 has no effect .
has no effect . - For
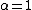 and
and  the distribution reduces to a Cauchy distributionCauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
the distribution reduces to a Cauchy distributionCauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
with scale parameter and shift parameter
and shift parameter 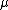 .
. - For
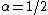 and
and 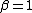 the distribution reduces to a Lévy distribution with scale parameter
the distribution reduces to a Lévy distribution with scale parameter  and shift parameter
and shift parameter 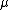 .
.
Note that the above three distributions are also connected, in the following way: A standard Cauchy random variable can be viewed as a mixture of Gaussian random variables (all with mean zero), with the variance being drawn from a standard Lévy distribution. And in fact this is a special case of a more general theorem which allows any symmetric alpha-stable distribution to be viewed in this way (with the alpha parameter of the mixture distribution equal to twice the alpha parameter of the mixing distribution—and the beta parameter of the mixing distribution always equal to one).
A general closed form expression for stable PDF's with rational values of α has been given by Zolotarev in terms of Meijer G-functionMeijer G-FunctionIn mathematics, the G-function was introduced by as a very general function intended to include most of the known special functions as particular cases. This was not the only attempt of its kind: the generalized hypergeometric function and the MacRobert E-function had the same aim, but Meijer's...
s. For simple rational numbers, the closed form expression is often in terms of less complicated special functionsSpecial functionsSpecial functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
. Lee has listed a number of closed form expressions having rather simple expressions in terms of special functions. In the table below, PDF's expressible by elementary functions are indicated by an E and those given by Lee that are expressible by special functions are indicated by an s.
α 1/3 1/2 2/3 1 4/3 3/2 2 β=0 s s s E Cauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
s s Holtsmark distributionThe Holtsmark distribution is a continuous probability distribution. The Holtsmark distribution is a special case of a stable distribution with the index of stability or shape parameter \alpha equal to 3/2 and skewness parameter \beta of zero. Since \beta equals zero, the distribution is...
E β=1 s E s s s
Some of the special cases are known by particular names:
- For
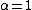 and
and 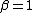 ,the distribution is a Landau distribution which has a specific usage in physics under this name.
,the distribution is a Landau distribution which has a specific usage in physics under this name. - For
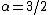 and
and 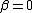 the distribution reduces to a Holtsmark distributionHoltsmark distributionThe Holtsmark distribution is a continuous probability distribution. The Holtsmark distribution is a special case of a stable distribution with the index of stability or shape parameter \alpha equal to 3/2 and skewness parameter \beta of zero. Since \beta equals zero, the distribution is...
the distribution reduces to a Holtsmark distributionHoltsmark distributionThe Holtsmark distribution is a continuous probability distribution. The Holtsmark distribution is a special case of a stable distribution with the index of stability or shape parameter \alpha equal to 3/2 and skewness parameter \beta of zero. Since \beta equals zero, the distribution is...
with scale parameter and shift parameter
and shift parameter 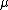 .
.
Also, in the limit as approaches zero or as
approaches zero or as  approaches zero the distribution will approach a Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
approaches zero the distribution will approach a Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
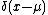 .
.
A generalized central limit theorem
Another important property of stable distributions is the role that they play in a generalized central limit theoremCentral limit theoremIn probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
. The central limit theorem states that the sum of a number of independent and identically distributed (i.i.d.) random variables with finite variances will tend to a normal distribution as the number of variables grows. A generalization due to GnedenkoBoris Vladimirovich GnedenkoBoris Vladimirovich Gnedenko was a Soviet mathematician and a student of Andrey Nikolaevich Kolmogorov. He was born in Simbirsk , Russia, and died in Moscow. He is perhaps best known for his work with Kolmogorov, and his contributions to the study of probability theory...
and Kolmogorov states that the sum of a number of random variables with power-law tail distributions decreasing as where
where 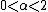 (and therefore having infinite variance) will tend to a stable distribution
(and therefore having infinite variance) will tend to a stable distribution 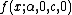 as the number of variables grows.
as the number of variables grows.
Series representation
The stable distribution can be restated as the real part of a simpler integral:
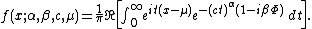
Expressing the second exponential as a Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
, we have:
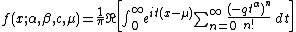
where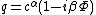 . Reversing the order of integration and summation, and carrying out the integration yields:
. Reversing the order of integration and summation, and carrying out the integration yields:
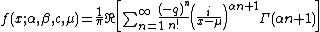
which will be valid for and will converge for appropriate values of the parameters. (Note that the n=0 term which yields a delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
and will converge for appropriate values of the parameters. (Note that the n=0 term which yields a delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
in has therefore been dropped.) Expressing the first exponential as a series will yield another series in positive powers of
has therefore been dropped.) Expressing the first exponential as a series will yield another series in positive powers of  which is generally less useful.
which is generally less useful.
See also
- Lévy flightLévy flightA Lévy flight is a random walk in which the step-lengths have a probability distribution that is heavy-tailed. When defined as a walk in a space of dimension greater than one, the steps made are in isotropic random directions...
- Lévy processLévy processIn probability theory, a Lévy process, named after the French mathematician Paul Lévy, is any continuous-time stochastic process that starts at 0, admits càdlàg modification and has "stationary independent increments" — this phrase will be explained below...
- Lévy distribution
- Fractional quantum mechanicsFractional quantum mechanicsIn physics, fractional quantum mechanics is a generalization of standard quantum mechanics. The term fractional quantum mechanics was coined by Nick Laskin...
- Other "power law" distributions
- Cauchy distributionCauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
(a special case of a stable distribution) - Pareto distribution
- Zeta distribution
- Zipf distribution
- Zipf–Mandelbrot distribution
- Cauchy distribution
- Stable and tempered stable distributions with volatility clustering – financial applications
- Multivariate stable distribution
External links
- PlanetMath stable random variable article
- John P. Nolan page on stable distributions
- stable distributions in GNU Scientific Library — Reference Manual
- Applications of stable laws in finance.
- fBasics RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
package with functions to compute stable density, distribution function, quantile function and generate random variates. - STBL MATLAB package which includes functions to compute stable densities, CDFs and inverse CDFs. Also can fit stable distributions to data, and generate stable random variables.
- StableDistribution is fully supported in MathematicaMathematicaMathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
since version 8.

