
Holtsmark distribution
Encyclopedia
The Holtsmark distribution is a continuous probability distribution. The Holtsmark distribution is a special case of a stable distribution with the index of stability or shape parameter  equal to 3/2 and skewness parameter
equal to 3/2 and skewness parameter 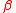 of zero. Since
of zero. Since 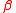 equals zero, the distribution is symmetric, and thus an example of a symmetric alpha-stable distribution. The Holtsmark distribution is one of the few examples of a stable distribution for which a closed form expression of the probability density function
equals zero, the distribution is symmetric, and thus an example of a symmetric alpha-stable distribution. The Holtsmark distribution is one of the few examples of a stable distribution for which a closed form expression of the probability density function
is known. However, its probability density function is not expressible in terms of elementary functions; rather, the probability density function is expressed in terms of hypergeometric functions.
The Holtsmark distribution has applications in plasma physics and astrophysics. In 1919, Norwegian physicist J. Holtsmark
proposed the distribution as a model for the fluctuating fields in plasma due to chaotic
motion of charged particles. It is also applicable to other types of Coulomb forces, in particular to modeling of gravitating bodies, and thus is important in astrophysics.
of a symmetric stable distribution is:
 equal to 3/2 and skewness parameter
equal to 3/2 and skewness parameter 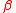 of zero. Since
of zero. Since 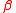 equals zero, the distribution is symmetric, and thus an example of a symmetric alpha-stable distribution. The Holtsmark distribution is one of the few examples of a stable distribution for which a closed form expression of the probability density function
equals zero, the distribution is symmetric, and thus an example of a symmetric alpha-stable distribution. The Holtsmark distribution is one of the few examples of a stable distribution for which a closed form expression of the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is known. However, its probability density function is not expressible in terms of elementary functions; rather, the probability density function is expressed in terms of hypergeometric functions.
The Holtsmark distribution has applications in plasma physics and astrophysics. In 1919, Norwegian physicist J. Holtsmark
Johan Peter Holtsmark
Johan Peter Holtsmark was a Norwegian physicist, who studied spectral line broadening and electron scattering. In 1929, while at the Norwegian Institute of Technology , Holtsmark established acoustics research laboratories, focusing on architectural acoustics and sound insulation...
proposed the distribution as a model for the fluctuating fields in plasma due to chaotic
Chaotic
Chaotic is originally a Danish trading card game. It expanded to an online game in America which then became a television program based on the game. The program is seen on 4Kids TV , Jetix, The CW4Kids, Cartoon Network and Disney XD. It was brought over to the United States from Denmark by Bryan C...
motion of charged particles. It is also applicable to other types of Coulomb forces, in particular to modeling of gravitating bodies, and thus is important in astrophysics.
Characteristic function
The characteristic functionCharacteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
of a symmetric stable distribution is:
-
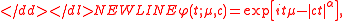
where is the shape parameter, or index of stability,
is the shape parameter, or index of stability,  is the location parameterLocation parameterIn statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
is the location parameterLocation parameterIn statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
, and c is the scale parameterScale parameterIn probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
.
Since the Holtsmark distribution has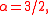 its characteristic function is:
its characteristic function is:
-
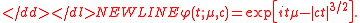
Since the Holtsmark distribution is a stable distribution with , represents the meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
represents the meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of the distribution. Since , also represents the medianMedianIn probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
also represents the medianMedianIn probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
and modeMode (statistics)In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
of the distribution. And since , the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the Holtsmark distribution is infinite. All higher momentsMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of the distribution are also infinite. Like other stable distributions (other than the normal distribution), since the variance is infinite the dispersion in the distribution is reflected by the scale parameterScale parameterIn probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
, c. An alternate approach to describing the dispersion of the distribution is through fractional moments.
Probability density function
In general, the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
, f(x), of a continuous probability distribution can be derived from its characteristic function by:

Most stable distributions do not have a known closed form expression for their probability density functions. Only the normal, CauchyCauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
and Lévy distributions have known closed form expressions in terms of elementary functions. The Holtsmark distribution is one of two symmetric stable distributions to have a known closed form expression in terms of hypergeometric functions. When is equal to 0 and the scale parameter is equal to 1, the Holtsmark distribution has the probability density function:
is equal to 0 and the scale parameter is equal to 1, the Holtsmark distribution has the probability density function:
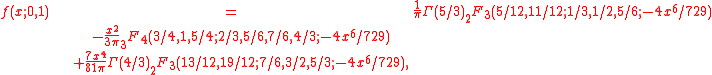
where is the gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
is the gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
and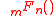 is a hypergeometric function.
is a hypergeometric function.
-

