
Zolotarev's lemma
Encyclopedia
In number theory
, Zolotarev's lemma states that the Legendre symbol
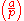
for an integer a modulo
an odd prime number
p, where p does not divide a, can be computed as the sign of a permutation:
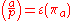
where ε denotes the signature of a permutation and πa is the permutation
of the nonzero residue classes mod p induced by multiplication by a.
For example, take a = 2 and p = 7. The nonzero squares mod 7 are 1, 2, and 4, so (2|7) = 1 and (6|7) = -1. Multiplication by 2 on the nonzero numbers mod 7 has the cycle decomposition (1,2,4)(3,6,5), so the sign of this permutation is 1, which is (2|7). Multiplication by 6 on the nonzero numbers mod 7 has cycle decomposition (1,6)(2,5)(3,4), whose sign is -1, which is (6|7).
G of order n, it is easy to determine the signature of the permutation πg made by left-multiplication by the element g of G. The permutation πg will be even, unless there are an odd number of orbits of even size. Assuming n even, therefore, the condition for πg to be an odd permutation, when g has order k, is that n/k should be odd, or that the subgroup generated by g should have odd index
.
We will apply this to the group of nonzero numbers mod p, which is a cyclic group
of order p-1. The jth power of a primitive root modulo p will by index calculus have index the greatest common divisor
The condition for a nonzero number mod p to be an quadratic non-residue is to be an odd power of a primitive root.
The lemma therefore comes down to saying that i is odd when j is odd, which is true a fortiori, and j is odd when i is odd, which is true because p − 1 is even (p is odd).
and vice versa. The example ,
,
i.e. the Legendre symbol (a/p) with a=3 and p=11, will illustrate how the proof goes. Start with the set {1,2,...,p-1} arranged as a matrix of two rows such that the sum of the two elements in any column is zero mod p, say:
Apply the permutation (mod p):
(mod p):
The columns still have the property that the sum of two elements in one column is zero mod p. Now apply a permutation V which swaps any pairs in which the upper member was originally a lower member:
Finally, apply a permutation W which gets back the original matrix:
We have W -1=VU. Zolotarev's lemma says (a/p)=1 iff the permutation U is even. Gauss's lemma says (a/p)=1 iff V is even. But W is even, so the two lemmas are equivalent for the given (but arbitrary) a and p.
the Jacobi symbol

where a and n are relatively prime odd integers with n > 0: a is invertible mod n, so multiplication by a on Z/nZ is a permutation and a generalization of Zolotarev's lemma is that the Jacobi symbol above is the sign of this permutation.
For example, multiplication by 2 on Z/21Z has cycle decomposition (0)(1,2,4,8,16,11)(3,6,12)(5,10,20,19,17,13)(7,14)(9,18,15), so the sign of this permutation is (1)(-1)(1)(-1)(-1)(1) = -1 and the Jacobi symbol (2|21) is -1. (Note that multiplication by 2 on the units mod 21 is a product of two 6-cycles, so its sign is 1. Thus it's important to use all integers mod n and not just the units mod n to define the right permutation.)
When n = p is an odd prime and a is not divisible by p, multiplication by a fixes 0 mod p, so the sign of multiplication by a on all numbers mod p and on the units mod p have the same sign. But for composite n that is not the case, as we see in the example above.
in an 1872 proof of quadratic reciprocity
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Zolotarev's lemma states that the Legendre symbol
Legendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
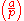
for an integer a modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
an odd prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, where p does not divide a, can be computed as the sign of a permutation:
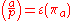
where ε denotes the signature of a permutation and πa is the permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the nonzero residue classes mod p induced by multiplication by a.
For example, take a = 2 and p = 7. The nonzero squares mod 7 are 1, 2, and 4, so (2|7) = 1 and (6|7) = -1. Multiplication by 2 on the nonzero numbers mod 7 has the cycle decomposition (1,2,4)(3,6,5), so the sign of this permutation is 1, which is (2|7). Multiplication by 6 on the nonzero numbers mod 7 has cycle decomposition (1,6)(2,5)(3,4), whose sign is -1, which is (6|7).
Proof
In general, for any finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
G of order n, it is easy to determine the signature of the permutation πg made by left-multiplication by the element g of G. The permutation πg will be even, unless there are an odd number of orbits of even size. Assuming n even, therefore, the condition for πg to be an odd permutation, when g has order k, is that n/k should be odd, or that the subgroup
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
.
We will apply this to the group of nonzero numbers mod p, which is a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order p-1. The jth power of a primitive root modulo p will by index calculus have index the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
- i = (j, p − 1).
The condition for a nonzero number mod p to be an quadratic non-residue is to be an odd power of a primitive root.
The lemma therefore comes down to saying that i is odd when j is odd, which is true a fortiori, and j is odd when i is odd, which is true because p − 1 is even (p is odd).
Another proof
Zolotarev's lemma can be deduced easily from Gauss's lemmaGauss's lemma (number theory)
Gauss's lemma in number theory gives a condition for an integer to be a quadratic residue. Although it is not useful computationally, it has theoretical significance, being involved in some proofs of quadratic reciprocity....
and vice versa. The example
 ,
,i.e. the Legendre symbol (a/p) with a=3 and p=11, will illustrate how the proof goes. Start with the set {1,2,...,p-1} arranged as a matrix of two rows such that the sum of the two elements in any column is zero mod p, say:
| 1 | 2 | 3 | 4 | 5 |
| 10 | 9 | 8 | 7 | 6 |
Apply the permutation
 (mod p):
(mod p):
| 3 | 6 | 9 | 1 | 4 |
| 8 | 5 | 2 | 10 | 7 |
The columns still have the property that the sum of two elements in one column is zero mod p. Now apply a permutation V which swaps any pairs in which the upper member was originally a lower member:
| 3 | 5 | 2 | 1 | 4 |
| 8 | 6 | 9 | 10 | 7 |
Finally, apply a permutation W which gets back the original matrix:
| 1 | 2 | 3 | 4 | 5 |
| 10 | 9 | 8 | 7 | 6 |
We have W -1=VU. Zolotarev's lemma says (a/p)=1 iff the permutation U is even. Gauss's lemma says (a/p)=1 iff V is even. But W is even, so the two lemmas are equivalent for the given (but arbitrary) a and p.
Jacobi Symbol
This interpretation of the Legendre symbol as the sign of a permutation can be extended tothe Jacobi symbol
Jacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...

where a and n are relatively prime odd integers with n > 0: a is invertible mod n, so multiplication by a on Z/nZ is a permutation and a generalization of Zolotarev's lemma is that the Jacobi symbol above is the sign of this permutation.
For example, multiplication by 2 on Z/21Z has cycle decomposition (0)(1,2,4,8,16,11)(3,6,12)(5,10,20,19,17,13)(7,14)(9,18,15), so the sign of this permutation is (1)(-1)(1)(-1)(-1)(1) = -1 and the Jacobi symbol (2|21) is -1. (Note that multiplication by 2 on the units mod 21 is a product of two 6-cycles, so its sign is 1. Thus it's important to use all integers mod n and not just the units mod n to define the right permutation.)
When n = p is an odd prime and a is not divisible by p, multiplication by a fixes 0 mod p, so the sign of multiplication by a on all numbers mod p and on the units mod p have the same sign. But for composite n that is not the case, as we see in the example above.
History
This lemma was introduced by Yegor Ivanovich ZolotarevYegor Ivanovich Zolotarev
Yegor Ivanovich Zolotarev was a Russian mathematician.- Biography :...
in an 1872 proof of quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
.
External links
- PlanetMath article on Zolotarev's lemma; includes his proof of quadratic reciprocity

