Zoltán Füredi
Encyclopedia
Zoltán Füredi is a Hungarian mathematician, working in combinatorics
, mainly in discrete geometry
and extremal combinatorics. He was a student of Gyula O. H. Katona
. He is a corresponding member of the Hungarian Academy of Sciences
(2004). He is a research professor of the Rényi Mathematical Institute
of the Hungarian Academy of Sciences, and a professor at the University of Illinois Urbana-Champaign (UIUC).
Füredi received his Candidate of Sciences degree in mathematics in 1981 from the Hungarian Academy of Sciences.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, mainly in discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
and extremal combinatorics. He was a student of Gyula O. H. Katona
Gyula O. H. Katona
Gyula O. H. Katona is a Hungarian mathematician known for his work in combinatorial set theory, and especially for the Kruskal–Katona theorem and his elegant proof of the Erdős–Ko–Rado theorem...
. He is a corresponding member of the Hungarian Academy of Sciences
Hungarian Academy of Sciences
The Hungarian Academy of Sciences is the most important and prestigious learned society of Hungary. Its seat is at the bank of the Danube in Budapest.-History:...
(2004). He is a research professor of the Rényi Mathematical Institute
Alfréd Rényi Institute of Mathematics
The Alfréd Rényi Institute of Mathematics is the research institute in mathematics of the Hungarian Academy of Sciences. It was created in 1950 by Alfréd Rényi, who directed it until his death. Since its creation, the institute has been the center of mathematical research in Hungary. It received...
of the Hungarian Academy of Sciences, and a professor at the University of Illinois Urbana-Champaign (UIUC).
Füredi received his Candidate of Sciences degree in mathematics in 1981 from the Hungarian Academy of Sciences.
Some results
- In infinitely many cases he determined the maximum number of edges in a graphGraph (mathematics)In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
with no C4Cycle graphIn graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
. - With Paul ErdősPaul ErdosPaul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
he proved that for some c>1, there are cd points in d-dimensional space such that all triangles formed from those points are acute. - With Imre BárányImre BárányImre Bárány is a Hungarian mathematician, working in combinatorics and discrete geometry. He works at the Rényi Mathematical Institute of the Hungarian Academy of Sciences, and has a part-time job at the University College London....
he proved that no polynomial time algorithm determines the volume of convex bodies in dimension d within a multiplicative error dd. - He proved that there are at least
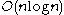unit distances among n points in the plane. - In a paper written with coauthors he solved the Hungarian lotteryLotteryA lottery is a form of gambling which involves the drawing of lots for a prize.Lottery is outlawed by some governments, while others endorse it to the extent of organizing a national or state lottery. It is common to find some degree of regulation of lottery by governments...
problem. - With I. Palásti he found the best known lower bounds on the orchard-planting problemOrchard-planting problemIn discrete geometry, the original orchard-planting problem asks for the maximum number of 3-point lines attainable by a configuration of points in the plane. Also called the Tree-planting problem, there are investigations into how many 4-, 5- & 6-point lines can be made...
of finding sets of points with many 3-point lines.