Zorn's lemma
Encyclopedia
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory
that states:
It is named after the mathematician
s Max Zorn
and Kazimierz Kuratowski
.
The terms are defined as follows. Suppose (P,≤) is a partially ordered set
. A subset T is totally ordered if for any s, t in T we have s ≤ t or t ≤ s. Such a set T has an upper bound u in P if t ≤ u for all t in T. Note that u is an element of P but need not be an element of T. An element m of P is called a maximal element if there is no element x in P for which m < x.
Note that P is not required to be non-empty.
However, the empty set is a chain (trivially), hence is required to have an upper bound, thus exhibiting at least one element of P.
An equivalent formulation of the lemma is therefore:
The distinction may seem subtle, but proofs involving Zorn's lemma often involve taking a union of some sort to produce an upper bound.
The case of an empty chain, hence empty union is a boundary case that is easily overlooked.
Zorn's lemma is equivalent to the well-ordering theorem
and the axiom of choice, in the sense that any one of them, together with the Zermelo–Fraenkel axioms of set theory
, is sufficient to prove the others. It occurs in the proofs of several theorems of crucial importance, for instance the Hahn–Banach theorem
in functional analysis
, the theorem that every vector space
has a basis
, Tychonoff's theorem
in topology
stating that every product of compact space
s is compact, and the theorems in abstract algebra
that every nonzero ring has a maximal ideal
and that every field
has an algebraic closure
.
. The set P here consists of all (two-sided) ideal
s in R except R itself, which is not empty since it contains at least the trivial ideal {0}. This set is partially ordered by set inclusion
. We are done if we can find a maximal element in P. The ideal R was excluded because maximal ideals by definition are not equal to R.
We want to apply Zorn's lemma, and so we take a non-empty totally ordered subset T of P and have to show that T has an upper bound, i.e. that there exists an ideal I ⊆ R which is bigger than all members of T but still smaller than R (otherwise it would not be in P). We take I to be the union
of all the ideals in T. Because T contains at least one element, and that element contains at least 0, the union I contains at least 0 and is not empty. Now to prove that I is an ideal: if a and b are elements of I, then there exist two ideals J, K ∈ T such that a is an element of J and b is an element of K. Since T is totally ordered, we know that J ⊆ K or K ⊆ J. In the first case, both a and b are members of the ideal K, therefore their sum a + b is a member of K, which shows that a + b is a member of I. In the second case, both a and b are members of the ideal J, and we conclude similarly that a + b ∈ I. Furthermore, if r ∈ R, then ar and ra are elements of J and hence elements of I. We have shown that I is an ideal in R.
Now comes the heart of the proof: why is I smaller than R? The crucial observation is that an ideal is equal to R if and only if
it contains 1. (It is clear that if it is equal to R, then it must contain 1; on the other hand, if it contains 1 and r is an arbitrary element of R, then r1 = r is an element of the ideal, and so the ideal is equal to R.) So, if I were equal to R, then it would contain 1, and that means one of the members of T would contain 1 and would thus be equal to R – but we explicitly excluded R from P.
The condition of Zorn's lemma has been checked, and we thus get a maximal element in P, in other words a maximal ideal in R.
Note that the proof depends on the fact that our ring R has a multiplicative unit 1. Without this, the proof wouldn't work and indeed the statement would be false. For example, the ring with
as additive group and trivial multiplication (i. e. 
for all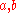 
) has no maximal ideal (and of course no 1): Its ideals are precisely the additive subgroups. The factor group 
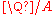by a proper subgroup 
is a divisible group
, hence certainly not finitely generated
, hence has a proper non-trivial subgroup, which gives rise to a subgroup and ideal containing
.
b, we need to employ the axiom of choice.
Using the function b, we are going to define elements a0 < a1 < a2 < a3 < ... in P. This sequence is really long: the indices are not just the natural number
s, but all ordinal
s. In fact, the sequence is too long for the set P (see Hartogs number
); there are too many ordinals, more than there are elements in any set, and the set P will be exhausted before long and then we will run into the desired contradiction.
The ai are defined by transfinite recursion: we pick a0 in P arbitrary (this is possible, since P contains an upper bound for the empty set and is thus not empty) and for any other ordinal w we set aw = b({av: v < w}). Because the av are totally ordered, this is a well-founded definition.
This proof shows that actually a slightly stronger version of Zorn's lemma is true:
is an early statement similar to Zorn's lemma.
K. Kuratowski
proved in 1922 a version of the lemma close to its modern formulation (it applied to sets ordered by inclusion and closed under unions of well-ordered chains). Essentially the same formulation (weakened by using arbitrary chains, not just well-ordered) was independently given by Max Zorn
in 1935, who proposed it as a new axiom
of set theory replacing the well-ordering theorem, exhibited some of its applications in algebra, and promised to show its equivalence with the axiom of choice in another paper, which never appeared.
The name "Zorn's lemma" appears to be due to John Tukey
, who used it in his book Convergence and Uniformity in Topology in 1940. Bourbaki's Théorie des Ensembles of 1939 refers to a similar maximal principle as "le théorème de Zorn". The name "Kuratowski–Zorn lemma" prevails in Poland and Russia.
) to three main results:
Moreover, Zorn's lemma (or one of its equivalent forms) implies some major results in other mathematical areas. For example,
In this sense, we see how Zorn's lemma can be seen as a powerful tool, especially in the sense of unified mathematics.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
that states:
Suppose a partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
P has the property that every chainTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
(i.e. totally orderedTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
) has an upper boundUpper boundIn mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
in P. Then the set P contains at least one maximal elementMaximal elementIn mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
.
It is named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s Max Zorn
Max August Zorn
Max August Zorn was a German-born American mathematician. He was an algebraist, group theorist, and numerical analyst. He is best known for Zorn's lemma, a powerful tool in set theory that is applicable to a wide range of mathematical constructs such as vector spaces, ordered sets, etc...
and Kazimierz Kuratowski
Kazimierz Kuratowski
Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...
.
The terms are defined as follows. Suppose (P,≤) is a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
. A subset T is totally ordered if for any s, t in T we have s ≤ t or t ≤ s. Such a set T has an upper bound u in P if t ≤ u for all t in T. Note that u is an element of P but need not be an element of T. An element m of P is called a maximal element if there is no element x in P for which m < x.
Note that P is not required to be non-empty.
However, the empty set is a chain (trivially), hence is required to have an upper bound, thus exhibiting at least one element of P.
An equivalent formulation of the lemma is therefore:
Suppose a non-empty partially ordered set P has the property that every non-empty chain has an upper bound in P. Then the set P contains at least one maximal element.
The distinction may seem subtle, but proofs involving Zorn's lemma often involve taking a union of some sort to produce an upper bound.
The case of an empty chain, hence empty union is a boundary case that is easily overlooked.
Zorn's lemma is equivalent to the well-ordering theorem
Well-ordering theorem
In mathematics, the well-ordering theorem states that every set can be well-ordered. A set X is well-ordered by a strict total order if every non-empty subset of X has a least element under the ordering. This is also known as Zermelo's theorem and is equivalent to the Axiom of Choice...
and the axiom of choice, in the sense that any one of them, together with the Zermelo–Fraenkel axioms of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, is sufficient to prove the others. It occurs in the proofs of several theorems of crucial importance, for instance the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the theorem that every vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
has a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, Tychonoff's theorem
Tychonoff's theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
stating that every product of compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
s is compact, and the theorems in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
that every nonzero ring has a maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
and that every field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
has an algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
.
An example application
We will go over a typical application of Zorn's lemma: the proof that every nontrivial ring R with unity contains a maximal idealMaximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
. The set P here consists of all (two-sided) ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
s in R except R itself, which is not empty since it contains at least the trivial ideal {0}. This set is partially ordered by set inclusion
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
. We are done if we can find a maximal element in P. The ideal R was excluded because maximal ideals by definition are not equal to R.
We want to apply Zorn's lemma, and so we take a non-empty totally ordered subset T of P and have to show that T has an upper bound, i.e. that there exists an ideal I ⊆ R which is bigger than all members of T but still smaller than R (otherwise it would not be in P). We take I to be the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of all the ideals in T. Because T contains at least one element, and that element contains at least 0, the union I contains at least 0 and is not empty. Now to prove that I is an ideal: if a and b are elements of I, then there exist two ideals J, K ∈ T such that a is an element of J and b is an element of K. Since T is totally ordered, we know that J ⊆ K or K ⊆ J. In the first case, both a and b are members of the ideal K, therefore their sum a + b is a member of K, which shows that a + b is a member of I. In the second case, both a and b are members of the ideal J, and we conclude similarly that a + b ∈ I. Furthermore, if r ∈ R, then ar and ra are elements of J and hence elements of I. We have shown that I is an ideal in R.
Now comes the heart of the proof: why is I smaller than R? The crucial observation is that an ideal is equal to R if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it contains 1. (It is clear that if it is equal to R, then it must contain 1; on the other hand, if it contains 1 and r is an arbitrary element of R, then r1 = r is an element of the ideal, and so the ideal is equal to R.) So, if I were equal to R, then it would contain 1, and that means one of the members of T would contain 1 and would thus be equal to R – but we explicitly excluded R from P.
The condition of Zorn's lemma has been checked, and we thus get a maximal element in P, in other words a maximal ideal in R.
Note that the proof depends on the fact that our ring R has a multiplicative unit 1. Without this, the proof wouldn't work and indeed the statement would be false. For example, the ring with
as additive group and trivial multiplication (i. e. for all 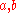) has no maximal ideal (and of course no 1): Its ideals are precisely the additive subgroups. The factor group 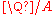by a proper subgroup is a divisible groupDivisible group
In mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
, hence certainly not finitely generated
Finitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
, hence has a proper non-trivial subgroup, which gives rise to a subgroup and ideal containing
.Sketch of the proof of Zorn's lemma (from the axiom of choice)
A sketch of the proof of Zorn's lemma follows. Suppose the lemma is false. Then there exists a partially ordered set, or poset, P such that every totally ordered subset has an upper bound, and every element has a bigger one. For every totally ordered subset T we may then define a bigger element b(T), because T has an upper bound, and that upper bound has a bigger element. To actually define the functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
b, we need to employ the axiom of choice.
Using the function b, we are going to define elements a0 < a1 < a2 < a3 < ... in P. This sequence is really long: the indices are not just the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, but all ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s. In fact, the sequence is too long for the set P (see Hartogs number
Hartogs number
In mathematics, specifically in axiomatic set theory, a Hartogs number is a particular kind of cardinal number. It was shown by Friedrich Hartogs in 1915, from ZF alone , that there is a least well-ordered cardinal greater than a given well-ordered cardinal.To define the Hartogs number of a set it...
); there are too many ordinals, more than there are elements in any set, and the set P will be exhausted before long and then we will run into the desired contradiction.
The ai are defined by transfinite recursion: we pick a0 in P arbitrary (this is possible, since P contains an upper bound for the empty set and is thus not empty) and for any other ordinal w we set aw = b({av: v < w}). Because the av are totally ordered, this is a well-founded definition.
This proof shows that actually a slightly stronger version of Zorn's lemma is true:
History
The Hausdorff maximal principleHausdorff maximal principle
In mathematics, the Hausdorff maximal principle is an alternate and earlier formulation of Zorn's lemma proved by Felix Hausdorff in 1914...
is an early statement similar to Zorn's lemma.
K. Kuratowski
Kazimierz Kuratowski
Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...
proved in 1922 a version of the lemma close to its modern formulation (it applied to sets ordered by inclusion and closed under unions of well-ordered chains). Essentially the same formulation (weakened by using arbitrary chains, not just well-ordered) was independently given by Max Zorn
Max August Zorn
Max August Zorn was a German-born American mathematician. He was an algebraist, group theorist, and numerical analyst. He is best known for Zorn's lemma, a powerful tool in set theory that is applicable to a wide range of mathematical constructs such as vector spaces, ordered sets, etc...
in 1935, who proposed it as a new axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
of set theory replacing the well-ordering theorem, exhibited some of its applications in algebra, and promised to show its equivalence with the axiom of choice in another paper, which never appeared.
The name "Zorn's lemma" appears to be due to John Tukey
John Tukey
John Wilder Tukey ForMemRS was an American statistician.- Biography :Tukey was born in New Bedford, Massachusetts in 1915, and obtained a B.A. in 1936 and M.Sc. in 1937, in chemistry, from Brown University, before moving to Princeton University where he received a Ph.D...
, who used it in his book Convergence and Uniformity in Topology in 1940. Bourbaki's Théorie des Ensembles of 1939 refers to a similar maximal principle as "le théorème de Zorn". The name "Kuratowski–Zorn lemma" prevails in Poland and Russia.
Equivalent forms of Zorn's lemma
Zorn's lemma is equivalent (in ZFZermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
) to three main results:
- Hausdorff maximal principleHausdorff maximal principleIn mathematics, the Hausdorff maximal principle is an alternate and earlier formulation of Zorn's lemma proved by Felix Hausdorff in 1914...
- Axiom of choice
- Well-ordering theoremWell-ordering theoremIn mathematics, the well-ordering theorem states that every set can be well-ordered. A set X is well-ordered by a strict total order if every non-empty subset of X has a least element under the ordering. This is also known as Zermelo's theorem and is equivalent to the Axiom of Choice...
.
Moreover, Zorn's lemma (or one of its equivalent forms) implies some major results in other mathematical areas. For example,
- Banach's extension theorem which is used to prove one of the most fundamental results in functional analysis, the Hahn–Banach theoremHahn–Banach theoremIn mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
- Every vector space has a Hamel basis, a result from linear algebra
- Every commutative unital ring has a maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
, a result from ring theory - Tychonoff's theoremTychonoff's theoremIn mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
in topology.
In this sense, we see how Zorn's lemma can be seen as a powerful tool, especially in the sense of unified mathematics.
External links
- Zorn's Lemma at ProvenMath contains a formal proof down to the finest detail of the equivalence of the axiom of choice and Zorn's Lemma.
- Zorn's Lemma at MetamathMetamathMetamath is a computer-assisted proof checker. It has no specific logic embedded and can simply be regarded as a device to apply inference rules to formulas...
is another formal proof. (Unicode version for recent browsers.)