
Śleszyński–Pringsheim theorem
Encyclopedia
In mathematics, the Śleszyński–Pringsheim theorem is a statement about convergence
of certain continued fraction
s. It was discovered by Ivan Śleszyński
and Alfred Pringsheim
in the late 19th century.
It states that if an, bn, for n = 1, 2, 3, ... are real number
s and |bn| ≥ |an| + 1 for all n, then
converges absolutely
to a number ƒ satisfying 0 < |ƒ| < 1, meaning that the series
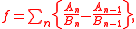
where An / Bn are the convergents
of the continued fraction, converges absolutely.
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
of certain continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s. It was discovered by Ivan Śleszyński
Ivan Sleszynski
Ivan Śleszyński was a Ukrainian-born Polish mathematician. Śleszyński's main work was on continued fractions, least squares and axiomatic proof theory based on mathematical logic. He and Alfred Pringsheim, working separately, proved what is now called the Śleszyński–Pringsheim theorem.-External...
and Alfred Pringsheim
Alfred Pringsheim
Alfred Israel Pringsheim was a German mathematician and patron of the arts. He was born in Ohlau, Prussian Silesia and died in Zürich, Switzerland.- Family and academic career :...
in the late 19th century.
It states that if an, bn, for n = 1, 2, 3, ... are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and |bn| ≥ |an| + 1 for all n, then
converges absolutely
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
to a number ƒ satisfying 0 < |ƒ| < 1, meaning that the series
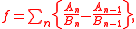
where An / Bn are the convergents
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
of the continued fraction, converges absolutely.


