*-autonomous category
Encyclopedia
In mathematics
, a *-autonomous (read "star-autonomous") category C is a symmetric monoidal closed category equipped with a dualizing object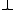
.
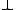, there exists a morphism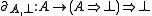
defined as the image by the bijection defining the monoidal closure, of the morphism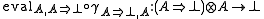
An object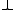
of the category C is called dualizing when the associated morphism 
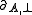is an isomorphism for every object A of the category C.
Equivalently, a *-autonomous category is a symmetric monoidal category C together with a functor
such that for every object A there is a natural isomorphism 
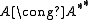, and for every three objects A, B and C there is a natural bijection
.
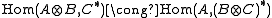The dualizing object of C is then defined by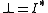
.
are *-autonomous, with the dual of the monoidal unit as the dualizing object, but *-autonomous categories need not to be compact closed
:
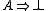is not necessarily a dual
of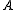
. However, if in a *-autonomous category we have
.
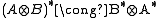for each pair (A,B) of objects, then the category is compact closed.
Various models of linear logic
form *-autonomous categories, the earliest of which was Jean-Yves Girard
's category of coherence spaces.
The category of complete semilattices
with morphisms preserving all joins but not necessarily meets is *-autonomous with dualizer the chain of two elements. A degenerate example (all homsets of cardinality at most one) is given by any Boolean algebra (as a partially ordered set
) made monoidal using conjunction for the tensor product and taking 0 as the dualizing object.
An example of a self-dual category that is not *-autonomous is finite linear orders and continuous functions, which has * but is not autonomous: its dualizing object is the two-element chain but there is no tensor product.
The category of sets and their partial injections is self-dual because the converse of the latter is again a partial injection.
The concept of *-autonomous category was introduced by Michael Barr
in 1979 in a monograph with that title. Barr defined the notion for the more general situation of V-categories, categories enriched in a symmetric monoidal or autonomous category V. The definition above specializes Barr's definition to the case V = Set of ordinary categories, those whose homobjects form sets (of morphisms). Barr's monograph includes an appendix by his student Po-Hsiang Chu which develops the details of a construction due to Barr showing the existence of nontrivial *-autonomous V-categories for all symmetric monoidal categories V with pullbacks, whose objects became known a decade later as Chu space
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a *-autonomous (read "star-autonomous") category C is a symmetric monoidal closed category equipped with a dualizing object
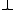.Definition
Let C be a symmetric monoidal closed category. For any object A and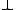, there exists a morphism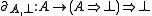defined as the image by the bijection defining the monoidal closure, of the morphism
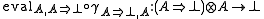
An object
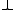of the category C is called dualizing when the associated morphism 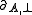is an isomorphism for every object A of the category C.Equivalently, a *-autonomous category is a symmetric monoidal category C together with a functor
such that for every object A there is a natural isomorphism 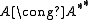, and for every three objects A, B and C there is a natural bijection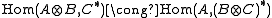.The dualizing object of C is then defined by
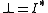.Properties
Compact closed categoriesCompact closed category
In category theory, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space...
are *-autonomous, with the dual of the monoidal unit as the dualizing object, but *-autonomous categories need not to be compact closed
Compact closed category
In category theory, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space...
:
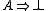is not necessarily a dualDual object
In category theory, a branch of mathematics, it is possible to define a concept of dual object generalizing the concept of dual space in linear algebra.A category in which each object has a dual is called autonomous or rigid.-Definition:...
of
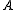. However, if in a *-autonomous category we have 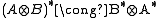.for each pair (A,B) of objects, then the category is compact closed.
Examples
A familiar example is given by matrix theory as finite-dimensional linear algebra, namely the category of finite-dimensional vector spaces over any field k made monoidal with the usual tensor product of vector spaces. The dualizing object is k, the one-dimensional vector space, and dualization corresponds to transposition. Although the category of all vector spaces over k is not *-autonomous, suitable extensions to categories of topological vector spaces can be made *-autonomous.Various models of linear logic
Linear logic
Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...
form *-autonomous categories, the earliest of which was Jean-Yves Girard
Jean-Yves Girard
Jean-Yves Girard is a French logician working in proof theory. His contributions include a proof of strong normalization in a system of second-order logic called system F; the invention of linear logic; the geometry of interaction; and ludics...
's category of coherence spaces.
The category of complete semilattices
Semilattice
In mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
with morphisms preserving all joins but not necessarily meets is *-autonomous with dualizer the chain of two elements. A degenerate example (all homsets of cardinality at most one) is given by any Boolean algebra (as a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
) made monoidal using conjunction for the tensor product and taking 0 as the dualizing object.
An example of a self-dual category that is not *-autonomous is finite linear orders and continuous functions, which has * but is not autonomous: its dualizing object is the two-element chain but there is no tensor product.
The category of sets and their partial injections is self-dual because the converse of the latter is again a partial injection.
The concept of *-autonomous category was introduced by Michael Barr
Michael Barr (mathematician)
Michael Barr is Peter Redpath Emeritus Professor of Pure Mathematics at McGill University. Although his earlier work was in homological algebra, his principal research area for a number of years has been category theory...
in 1979 in a monograph with that title. Barr defined the notion for the more general situation of V-categories, categories enriched in a symmetric monoidal or autonomous category V. The definition above specializes Barr's definition to the case V = Set of ordinary categories, those whose homobjects form sets (of morphisms). Barr's monograph includes an appendix by his student Po-Hsiang Chu which develops the details of a construction due to Barr showing the existence of nontrivial *-autonomous V-categories for all symmetric monoidal categories V with pullbacks, whose objects became known a decade later as Chu space
Chu space
Chu spaces generalize the notion of topological space by dropping the requirements that the set of open sets be closed under union and finite intersection, that the open sets be extensional, and that the membership predicate be two-valued...
s.