-yllion
Encyclopedia
-yllion is a proposal from Donald Knuth
for the terminology and symbols of an alternate decimal superbase system. In it, he adapts the familiar English terms for large numbers
to provide a systematic set of names for much larger numbers
. In addition to providing an extended range, -yllion also dodges the long and short scale
ambiguity of -illion.
Knuth's digit grouping is exponential
instead of linear; each division doubles the number of digits handled, whereas the familiar system only adds three or six more. His system is basically the same as one of the ancient and now-unused Chinese numeral systems
, in which units stand for 104, 108, 1016, 1032, and so on.
In Knuth's -yllion proposal:
Each new number name is the square of the previous one — therefore, each new name covers twice as many digits. Knuth continues borrowing the traditional names changing "illion" to "yllion" on each one.
Abstractly, then, "one n-yllion" is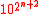
. "One trigintyllion" (
) would have nearly forty-three myllion (4300 million) digits. (By contrast, a conventional "trigintillion" has merely 94 digits — not even a hundred, let alone a hundred million!)
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
for the terminology and symbols of an alternate decimal superbase system. In it, he adapts the familiar English terms for large numbers
Large numbers
This article is about large numbers in the sense of numbers that are significantly larger than those ordinarily used in everyday life, for instance in simple counting or in monetary transactions...
to provide a systematic set of names for much larger numbers
Names of large numbers
This article lists and discusses the usage and derivation of names of large numbers, together with their possible extensions.The following table lists those names of large numbers which are found in many English dictionaries and thus have a special claim to being "real words"...
. In addition to providing an extended range, -yllion also dodges the long and short scale
Long and short scales
The long and short scales are two of several different large-number naming systems used throughout the world for integer powers of ten. Many countries, including most in continental Europe, use the long scale whereas most English-speaking countries use the short scale...
ambiguity of -illion.
Knuth's digit grouping is exponential
Scientific notation
Scientific notation is a way of writing numbers that are too large or too small to be conveniently written in standard decimal notation. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians, doctors, and engineers.In scientific...
instead of linear; each division doubles the number of digits handled, whereas the familiar system only adds three or six more. His system is basically the same as one of the ancient and now-unused Chinese numeral systems
Chinese numerals
Chinese numerals are characters for writing numbers in Chinese. Today speakers of Chinese use three numeral systems:the ubiquitous Arabic numerals and two indigenous systems....
, in which units stand for 104, 108, 1016, 1032, and so on.
Details and examples
For a more extensive table, see Myriad system.| Value | Name | Notation |
|---|---|---|
| 100 | One | 1 |
| 101 | Ten | 10 |
| 102 | Hundred | 100 |
| 103 | Ten hundred | 1000 |
| 104 | Myriad | 1,0000 |
| 105 | Ten myriad | 10,0000 |
| 106 | Hundred myriad | 100,0000 |
| 107 | Ten hundred myriad | 1000,0000 |
| 108 | Myllion | 1;0000,0000 |
| 1012 | Myriad myllion | 1,0000;0000,0000 |
| 1016 | Byllion | 1:0000,0000;0000,0000 |
| 1024 | Myllion byllion | 1;0000,0000:0000,0000;0000,0000 |
| 1032 | Tryllion | 1 0000,0000;0000,0000:0000,0000;0000,0000 |
| 1064 | Quadryllion | 1'0000,0000;0000,0000:0000,0000;0000,0000 0000,0000;0000,0000:0000,0000;0000,0000 |
| 10128 | Quintyllion | 1 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 |
| 10256 | Sextyllion | 1 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 |
In Knuth's -yllion proposal:
- 1 to 999 have their usual names.
- 1000 to 9999 are divided before the 2nd-last digit and named "blahPlaceholder namePlaceholder names are words that can refer to objects or people whose names are either temporarily forgotten, irrelevant, or unknown in the context in which they are being discussed...
hundred blah." (e.g. 1234 is "twelve hundred thirty-four"; 7623 is "seventy-six hundred twenty-three") - 104 to 108-1 are divided before the 4th-last digit and named "blah myriadMyriadMyriad , "numberlesscountless, infinite", is a classical Greek word for the number 10,000. In modern English, the word refers to an unspecified large quantity.-History and usage:...
blah". Knuth also introduces at this level a grouping symbol (comma) for the numeral. So, 382,1902 is "three hundred eighty-two myriad nineteen hundred two." - 108 to 1016-1 are divided before the 8th-last digit and named "blah myllion blah", and a semicolon separates the digits. So 1,0002;0003,0004 is "one myriad two myllion, three myriad four."
- 1016 to 1032-1 are divided before the 16th-last digit and named "blah byllion blah", and a colon separates the digits. So 12:0003,0004;0506,7089 is "twelve byllion, three myriad four myllion, five hundred six myriad seventy hundred eighty-nine."
- etc.
Each new number name is the square of the previous one — therefore, each new name covers twice as many digits. Knuth continues borrowing the traditional names changing "illion" to "yllion" on each one.
Abstractly, then, "one n-yllion" is
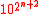. "One trigintyllion" () would have nearly forty-three myllion (4300 million) digits. (By contrast, a conventional "trigintillion" has merely 94 digits — not even a hundred, let alone a hundred million!)See also
- Alternatives to Knuth's proposal that date back to the French RenaissanceFrench RenaissanceFrench Renaissance is a recent term used to describe a cultural and artistic movement in France from the late 15th century to the early 17th century. It is associated with the pan-European Renaissance that many cultural historians believe originated in northern Italy in the fourteenth century...
came from Nicolas ChuquetNicolas ChuquetNicolas Chuquet was a French mathematician whose great work, Triparty en la science des nombres , was unpublished in his lifetime...
and Jacques Peletier du MansJacques Peletier du MansJacques Pelletier du Mans, also spelled Peletier, in Latin: Peletarius , was a humanist, poet and mathematician of the French Renaissance....
. - A related proposal by Knuth is his up-arrow notationKnuth's up-arrow notationIn mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
. - The Sand ReckonerThe Sand ReckonerThe Sand Reckoner is a work by Archimedes in which he set out to determine an upper bound for the number of grains of sand that fit into the universe. In order to do this, he had to estimate the size of the universe according to the then-current model, and invent a way to talk about extremely...