
6-simplex honeycomb
Encyclopedia
| 6-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform honeycomb Convex uniform honeycomb In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;... |
| Family | Simplectic honeycomb |
| Schläfli symbol | {3[7]} |
| Coxeter–Dynkin diagrams | |
| 6-face types | {3,3,3,3,3} t1{3,3,3,3,3} Rectified 6-simplex In six-dimensional geometry, a rectified 6-simplex is a convex uniform 6-polytope, being a rectification of the regular 6-simplex.There are three unique degrees of rectifications, including the zeroth, the 6-simplex itself. Vertices of the rectified 6-simplex are located at the edge-centers of the... t2{3,3,3,3,3} |
| 5-face types | {3,3,3,3} t1{3,3,3,3} t2{3,3,3,3} |
| 4-face types | {3,3,3} t1{3,3,3} Rectified 5-cell In four dimensional geometry, the rectified 5-cell is a uniform polychoron composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In total it has 30 triangle faces, 30 edges, and 10... |
| Cell types | {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... t1{3,3} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
| Face types | {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
| Vertex figure | t05{35} Pentellated 6-simplex In six-dimensional geometry, a pentellated 6-simplex is a convex uniform 6-polytope with 5th order truncations of the regular 6-simplex.There are unique 10 degrees of pentellations of the 6-simplex with permutations of truncations, cantellations, runcinations, and sterications... |
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... s |
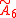 , [3[7]] , [3[7]] |
| Properties | vertex-transitive Vertex-transitive In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same... |
In six-dimensional
Sixth dimension
Six-dimensional space is any space that has six dimensions, that is, six degrees of freedom, and that needs six pieces of data, or coordinates, to specify a location in this space. There are an infinite number of these, but those of most interest are simpler ones that model some aspect of the...
Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, the 6-simplex honeycomb is a space-filling tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
(or honeycomb
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
). The tessellation fills space by 6-simplex, rectified 6-simplex
Rectified 6-simplex
In six-dimensional geometry, a rectified 6-simplex is a convex uniform 6-polytope, being a rectification of the regular 6-simplex.There are three unique degrees of rectifications, including the zeroth, the 6-simplex itself. Vertices of the rectified 6-simplex are located at the edge-centers of the...
, and birectified 6-simplex facets. These facet types occur in proportions of 1:1:1 respectively in the whole honeycomb.
This vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
is called the A6 lattice or 6-simplex lattice. The 42 vertices of the expanded 6-simplex vertex figure represent the 42 roots of the
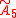 Coxeter group.
Coxeter group.Related polytopes and honeycombs
This honeycomb is one of 17 unique uniform honycombs constructed bythe
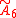 Coxeter group
Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
. The Coxeter–Dynkin diagrams of the others are:
See also
- Regular and uniform honeycombs in 5-space:
- 6-cubic honeycomb
- 6-demicubic honeycomb

