Abductive logic programming
Encyclopedia
Abductive logic programming (ALP) is a high level knowledge-representation framework that can be used to solve problems declaratively based on abductive reasoning
. It extends normal logic programming
by allowing some predicates to be incompletely defined, declared as abducible predicates. Problem solving is effected by deriving hypotheses on these abducible predicates (abductive hypotheses) as solutions of problems to be solved. These problems can be either observations that need to be explained (as in classical abduction) or goals to be achieved (as in normal logic programming
). It can be used to solve problems in Diagnosis, Planning
, Natural Language and Machine Learning
. It has also been used to interpret Negation as failure as a form of abductive reasoning.
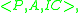where:
Normally, the logic program P does not contain any clauses whose head (or conclusion) refers to an abducible predicate. (This restriction can be made without loss of generality.) Also in practice, many times the integrity constraints
in IC are often restricted to the form of denials, i.e. clauses of the form:
false:- A1,...,An, not B1, ..., not Bm.
Such a constraint means that it is not possible for all A1,...,An to be true and at the same time all of B1,...,Bm to be false.
A problem, G, which expresses either an observation that needs to be explained or a goal that is desired, is represented
by a conjunction of positive and negative (NAF) literals. Such problems are solved by computing "abductive explanations" of G.
An abductive explanation of a problem G is a set of positive (and sometimes also negative) ground instances of the abducible predicates, such that, when these are added to the logic program P, the problem G and the integrity constraints IC both hold. Thus abductive explanations extend the logic program P by the addition of full or partial definitions of the abducible predicates. In this way, abductive explanations form solutions of the problem according to the description of the problem domain in P and IC. The extension or completion of the problem description given by the abductive explanations provides new information, hitherto not contained in the solution to the problem. Quality criteria to prefer one solution over another, often expressed via integrity constraints, can be applied to select specific abductive explanations of the problem G.
Computation in ALP combines the backwards reasoning of normal logic programming (to reduce problems to sub-problems) with a kind of integrity checking to show that the abductive explanations satisfy the integrity constraints.
The following two examples, written in simple structured English rather than in the strict syntax of ALP, illustrate the notion
of abductive explanation in ALP and its relation to problem solving.
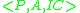, has in 
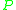the following sentences:
Grass is wet if it rained.
Grass is wet if the sprinkler was on.
The sun was shining.
The abducible predicates in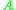
are "it rained" and "the sprinkler was on" and the only integrity constraintin in 
is:
false if it rained and the sun was shining.
The observation that the grass is wet has two potential explanations, "it rained" and "the sprinkler was on", which entail the observation. However, only the second potential explanation, "the sprinkler was on", satisfies the integrity constraint.
X is a citizen if X is born in the USA.
X is a citizen if X is born outside the USA and X is a resident of the USA and X is naturalized.
X is a citizen if X is born outside the USA and Y is the mother of X and Y is a citizen and X is registered.
Mary is the mother of John.
Mary is a citizen.
together with the five abducible predicates, "is born in the USA", "is born outside the USA", "is a resident of the USA", "is naturalized" and "is registered" and the integrity constraint:
false if John is a resident of the USA.
The goal "John is citizen" has two abductive solutions, one of which is "John is born in the USA", the other of which is "John is born outside the USA" and "John is registered". The potential solution of becoming a citizen by residence and naturalization fails because it violates the integrity constraint.
A more complex example that is also written in the more formal syntax of ALP is the following.
and lactose are high or when they are both at medium level. The abducibles, A, declare all ground instances of the predicates "amount" as assumable. This reflects the fact that in the model the amounts at any time of the various substances are unknown. This is incomplete information that is to be determined in each problem case.
The integrity constraints state that the amount of a substance (S) can only take one value.
Domain Knowledge (P)
feed(lactose):-make(permease),make(galactosidase).
make(Enzyme):-code(Gene,Enzyme),express(Gene).
express(lac(X)):-amount(glucose,low),amount(lactose,hi).
express(lac(X)):-amount(glucose,medium),amount(lactose,medium).
code(lac(y),permease).
code(lac(z),galactosidase).
temperature(low):-amount(glucose,low).
Integrity Constraints (IC)
false :- amount(S,V1), amount(S,V2), V1
V2.
Abducibles (A)
abducible_predicate(amount).
The problem goal is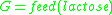
. This can arise either as an observation to be explained or as a state of affairs to be achieved by finding a plan. This goal has two abductive explanations:
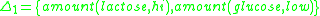
The decision which of the two to adopt could depend on addition information that is available, e.g. it may be known that when the level of glucose is low then the organism exhibits a certain behaviour - in the model such additional information is that the temperature of the organism is low - and by observing the truth or falsity of this it is possible to choose the first or second explanation respectively.
Once an explanation has been chosen, then this becomes part of the theory, which can be used to draw new conclusions. The explanation and more generally these new conclusions form the solution of the problem.
Given an abductive logic program,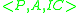
, an abductive explanation for a problem 
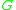is a set 
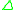of ground atoms on abducible predicates such that:
-
-
-
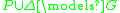
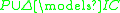
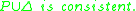
This definition is generic in the underlying semantics of logic programming. Each particular choice of semantics defines its own entailment
relation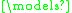
, its own notion of consistent logic programs and hence its own notion of what an abductive solution is. In practice, the three main semantics of logic programming --- completion, stable and well-founded semantics --- have been used to define different ALP frameworks.
The integrity constraints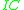
define how they constrain the abductive solutions. There are different views on this. Early work on abduction in Theorist in the context of classical logic was based on the consistency view on constraints. In this view, any extension of the given theory with an abductive solution 
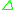is required to be consistent with the integrity constraints IC: 
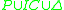is consistent. The above definition formalizes the entailment view: the abductive solution 
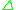together with 
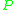should entail the constraints. This view is the one taken in most versions of ALP and is stronger than the consistency view in the sense that a solution according to the entailment view is a solution according to the consistency view but not vice versa.
The difference between the two views can be subtle but in practice the different views usually coincide. E.g. it frequently happens that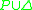
has a unique model, in which case the two views are equivalent. In practice, many ALP systems use the entailment view as this can be easily implemented without the need for any extra specialized procedures for the satisfaction of the integrity constraints since this semantics treats the constraints in the same way as the goal.
and Bayesian networks as special cases.
There exist strong links between some ALP frameworks and other extensions of logic programming. In particular, ALP has close connections with Answer Set Programming. An abductive logic program can be translated into an equivalent answer set program under the stable model semantics. Consequently, systems for computing stable models such as SMODELS can be used to compute abduction in ALP.
ALP is also closely related to constraint logic programming (CLP). On the one hand, the integration of constraint solving and abductive logic programming enhances the practical utility of ALP through a more efficient computation of abduction. On the other hand, the integration of ALP and CLP can be seen as a high-level constraint programming environment that allows more modular and flexible representations of the problem domain.
There is also a strong link between ALP and Argumentation in logic programming. This relates both to the interpretation of Negation as Failure and Integrity Constraints.
Abductive reasoning
Abduction is a kind of logical inference described by Charles Sanders Peirce as "guessing". The term refers to the process of arriving at an explanatory hypothesis. Peirce said that to abduce a hypothetical explanation a from an observed surprising circumstance b is to surmise that a may be true...
. It extends normal logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
by allowing some predicates to be incompletely defined, declared as abducible predicates. Problem solving is effected by deriving hypotheses on these abducible predicates (abductive hypotheses) as solutions of problems to be solved. These problems can be either observations that need to be explained (as in classical abduction) or goals to be achieved (as in normal logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
). It can be used to solve problems in Diagnosis, Planning
Planning
Planning in organizations and public policy is both the organizational process of creating and maintaining a plan; and the psychological process of thinking about the activities required to create a desired goal on some scale. As such, it is a fundamental property of intelligent behavior...
, Natural Language and Machine Learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
. It has also been used to interpret Negation as failure as a form of abductive reasoning.
Syntax
Abductive logic programs have three components,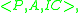 where:- P is a logic program of exactly the same form as in Logic Programming
- A is a set of predicate names, called the abducible predicates
- IC is a set of first order classical formulae.
Normally, the logic program P does not contain any clauses whose head (or conclusion) refers to an abducible predicate. (This restriction can be made without loss of generality.) Also in practice, many times the integrity constraints
Integrity constraints
Integrity constraints are used to ensure accuracy and consistency of data in a relational database. Data integrity is handled in a relational database through the concept of referential integrity...
in IC are often restricted to the form of denials, i.e. clauses of the form:
false:- A1,...,An, not B1, ..., not Bm.
Such a constraint means that it is not possible for all A1,...,An to be true and at the same time all of B1,...,Bm to be false.
Informal meaning and problem solving
The clauses in P define a set of non-abducible predicates and through this they provide a description (or model) of the problem domain. The integrity constraints in IC specify general properties of the problem domain that need to be respected in any solution of our problem.A problem, G, which expresses either an observation that needs to be explained or a goal that is desired, is represented
by a conjunction of positive and negative (NAF) literals. Such problems are solved by computing "abductive explanations" of G.
An abductive explanation of a problem G is a set of positive (and sometimes also negative) ground instances of the abducible predicates, such that, when these are added to the logic program P, the problem G and the integrity constraints IC both hold. Thus abductive explanations extend the logic program P by the addition of full or partial definitions of the abducible predicates. In this way, abductive explanations form solutions of the problem according to the description of the problem domain in P and IC. The extension or completion of the problem description given by the abductive explanations provides new information, hitherto not contained in the solution to the problem. Quality criteria to prefer one solution over another, often expressed via integrity constraints, can be applied to select specific abductive explanations of the problem G.
Computation in ALP combines the backwards reasoning of normal logic programming (to reduce problems to sub-problems) with a kind of integrity checking to show that the abductive explanations satisfy the integrity constraints.
The following two examples, written in simple structured English rather than in the strict syntax of ALP, illustrate the notion
of abductive explanation in ALP and its relation to problem solving.
Example 1
The abductive logic program,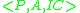, has in 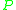the following sentences:Grass is wet if it rained.
Grass is wet if the sprinkler was on.
The sun was shining.
The abducible predicates in
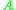are "it rained" and "the sprinkler was on" and the only integrity constraintin in is:false if it rained and the sun was shining.
The observation that the grass is wet has two potential explanations, "it rained" and "the sprinkler was on", which entail the observation. However, only the second potential explanation, "the sprinkler was on", satisfies the integrity constraint.
Example 2
Consider the abductive logic program consisting of the following (simplified) clauses:X is a citizen if X is born in the USA.
X is a citizen if X is born outside the USA and X is a resident of the USA and X is naturalized.
X is a citizen if X is born outside the USA and Y is the mother of X and Y is a citizen and X is registered.
Mary is the mother of John.
Mary is a citizen.
together with the five abducible predicates, "is born in the USA", "is born outside the USA", "is a resident of the USA", "is naturalized" and "is registered" and the integrity constraint:
false if John is a resident of the USA.
The goal "John is citizen" has two abductive solutions, one of which is "John is born in the USA", the other of which is "John is born outside the USA" and "John is registered". The potential solution of becoming a citizen by residence and naturalization fails because it violates the integrity constraint.
A more complex example that is also written in the more formal syntax of ALP is the following.
Example 3
The abductive logic program below describes a simple model of the lactose metabolism of the bacterium E. Coli. The program P describes the fact that E. coli can feed on the sugar lactose if it makes two enzymes permease and galactosidase. Like all enzymes (E), these are made if they are coded by a gene (G) that is expressed. These enzymes are coded by two genes (lac(y) and lac(z)) in cluster of genes (lac(X)) – called an operon – that is expressed when the amounts (amt) of glucose are lowand lactose are high or when they are both at medium level. The abducibles, A, declare all ground instances of the predicates "amount" as assumable. This reflects the fact that in the model the amounts at any time of the various substances are unknown. This is incomplete information that is to be determined in each problem case.
The integrity constraints state that the amount of a substance (S) can only take one value.
Domain Knowledge (P)
feed(lactose):-make(permease),make(galactosidase).
make(Enzyme):-code(Gene,Enzyme),express(Gene).
express(lac(X)):-amount(glucose,low),amount(lactose,hi).
express(lac(X)):-amount(glucose,medium),amount(lactose,medium).
code(lac(y),permease).
code(lac(z),galactosidase).
temperature(low):-amount(glucose,low).
Integrity Constraints (IC)
false :- amount(S,V1), amount(S,V2), V1
V2.Abducibles (A)
abducible_predicate(amount).
The problem goal is
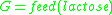. This can arise either as an observation to be explained or as a state of affairs to be achieved by finding a plan. This goal has two abductive explanations: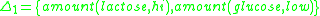The decision which of the two to adopt could depend on addition information that is available, e.g. it may be known that when the level of glucose is low then the organism exhibits a certain behaviour - in the model such additional information is that the temperature of the organism is low - and by observing the truth or falsity of this it is possible to choose the first or second explanation respectively.
Once an explanation has been chosen, then this becomes part of the theory, which can be used to draw new conclusions. The explanation and more generally these new conclusions form the solution of the problem.
Formal semantics
The formal semantics of the central notion of an abductive explanation in ALP, can be defined in the following way:Given an abductive logic program,
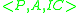, an abductive explanation for a problem 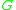is a set 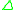of ground atoms on abducible predicates such that:-
-
-
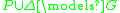
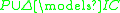
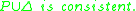
This definition is generic in the underlying semantics of logic programming. Each particular choice of semantics defines its own entailment
Entailment
In logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
relation
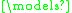, its own notion of consistent logic programs and hence its own notion of what an abductive solution is. In practice, the three main semantics of logic programming --- completion, stable and well-founded semantics --- have been used to define different ALP frameworks.The integrity constraints
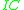define how they constrain the abductive solutions. There are different views on this. Early work on abduction in Theorist in the context of classical logic was based on the consistency view on constraints. In this view, any extension of the given theory with an abductive solution 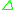is required to be consistent with the integrity constraints IC: 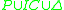is consistent. The above definition formalizes the entailment view: the abductive solution 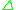together with 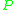should entail the constraints. This view is the one taken in most versions of ALP and is stronger than the consistency view in the sense that a solution according to the entailment view is a solution according to the consistency view but not vice versa.The difference between the two views can be subtle but in practice the different views usually coincide. E.g. it frequently happens that
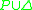has a unique model, in which case the two views are equivalent. In practice, many ALP systems use the entailment view as this can be easily implemented without the need for any extra specialized procedures for the satisfaction of the integrity constraints since this semantics treats the constraints in the same way as the goal.Comparison with other frameworks
ALP can be viewed as a refinement of Theorist, which explored the use of abduction in first-order logic for both explanation and default reasoning. David Poole later developed a logic programming variant of Theorist, in which abducible predicates have associated probabilities. He showed that probabilistic Horn abduction incorporates both pure PrologProlog
Prolog is a general purpose logic programming language associated with artificial intelligence and computational linguistics.Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is declarative: the program logic is expressed in terms of...
and Bayesian networks as special cases.
There exist strong links between some ALP frameworks and other extensions of logic programming. In particular, ALP has close connections with Answer Set Programming. An abductive logic program can be translated into an equivalent answer set program under the stable model semantics. Consequently, systems for computing stable models such as SMODELS can be used to compute abduction in ALP.
ALP is also closely related to constraint logic programming (CLP). On the one hand, the integration of constraint solving and abductive logic programming enhances the practical utility of ALP through a more efficient computation of abduction. On the other hand, the integration of ALP and CLP can be seen as a high-level constraint programming environment that allows more modular and flexible representations of the problem domain.
There is also a strong link between ALP and Argumentation in logic programming. This relates both to the interpretation of Negation as Failure and Integrity Constraints.
Implementation and systems
Most of the implementations of ALP extend the SLD resolution based computational model of logic programming. ALP can also be implemented by means on its link with Answer Set Programming (ASP), where the ASP systems can be employed. Examples of systems of the former approach are ACLP, A-system, CIFF, SCIFF, ABDUAL and ProLogICA.See also
- Abductive reasoningAbductive reasoningAbduction is a kind of logical inference described by Charles Sanders Peirce as "guessing". The term refers to the process of arriving at an explanatory hypothesis. Peirce said that to abduce a hypothetical explanation a from an observed surprising circumstance b is to surmise that a may be true...
- Answer set programmingAnswer set programmingAnswer set programming is a form of declarative programming oriented towards difficult search problems. It is based on the stable model semantics of logic programming. In ASP, search problems are reduced to computing stable models, and answer set solvers -- programs for generating stable...
- Inductive logic programmingInductive logic programmingInductive logic programming is a subfield of machine learning which uses logic programming as a uniform representation for examples, background knowledge and hypotheses...
- Negation as failure
- Argumentation