
Abductive reasoning
Encyclopedia
Abduction is a kind of logical inference described by Charles Sanders Peirce as "guessing". The term refers to the process of arriving at an explanatory hypothesis. Peirce said that to abduce a hypothetical explanation  from an observed surprising circumstance
from an observed surprising circumstance  is to surmise that
is to surmise that  may be true because then
may be true because then  would be a matter of course. Thus, to abduce
would be a matter of course. Thus, to abduce  from
from  involves determining that
involves determining that  is sufficient (or nearly sufficient), but not necessary
is sufficient (or nearly sufficient), but not necessary
, for .
.
For example, the lawn is wet. But if it rained last night, then it would be unsurprising that the lawn is wet. Therefore, by abductive reasoning, the possibility that it rained last night is reasonable. (But note that Peirce did not remain convinced that a single logical form covers all abduction.)
Peirce argues that good abductive reasoning from P to Q involves not simply a determination that, e.g., Q is sufficient for P, but also that Q is among the most economical explanation
s for P. Simplification and economy are what call for the 'leap' of abduction.
There has been renewed interest in the subject of abduction in the fields of computer science and artificial intelligence research.
: allows deriving from
from  only where
only where  is a formal consequence of
is a formal consequence of  . In other words, deduction is the process of deriving the consequences of what is assumed. Given the truth of the assumptions, a valid deduction guarantees the truth of the conclusion. For example, given that all bachelors are unmarried males, and given that this person is a bachelor, it can be deduced that this person is an unmarried male.
. In other words, deduction is the process of deriving the consequences of what is assumed. Given the truth of the assumptions, a valid deduction guarantees the truth of the conclusion. For example, given that all bachelors are unmarried males, and given that this person is a bachelor, it can be deduced that this person is an unmarried male.
Induction
: allows inferring from
from  , where
, where  does not follow necessarily from
does not follow necessarily from  .
.  might give us very good reason to accept
might give us very good reason to accept  , but it does not ensure that
, but it does not ensure that  . For example, if all of the swans that we have observed so far are white, we may induce that the possibility that all swans are white is reasonable. We have good reason to believe the conclusion from the premise, but the truth of the conclusion is not guaranteed. (Indeed, it turns out that some swans are black
. For example, if all of the swans that we have observed so far are white, we may induce that the possibility that all swans are white is reasonable. We have good reason to believe the conclusion from the premise, but the truth of the conclusion is not guaranteed. (Indeed, it turns out that some swans are black
.)
Abduction : allows inferring as an explanation of
as an explanation of  . Because of this, abduction allows the precondition
. Because of this, abduction allows the precondition  to be abduced from the consequence
to be abduced from the consequence  . Deduction
. Deduction
and abduction thus differ in the direction in which a rule like " entail
entail
s " is used for inference. As such abduction is formally equivalent to the logical fallacy affirming the consequent
" is used for inference. As such abduction is formally equivalent to the logical fallacy affirming the consequent
or Post hoc ergo propter hoc
, because there are multiple possible explanations for . For example, after glancing up and seeing the eight ball moving towards us we may abduce that it was struck by the cue ball. The cue ball's strike would account for the eight ball's movement. It serves as a hypothesis that explains our observation. There are in fact infinitely many possible explanations for the eight ball's movement, and so our abduction does not leave us certain that the cue ball did in fact strike the eight ball, but our abduction is still useful and can serve to orient us in our surroundings. This process of abduction is an instance of the scientific method. There are infinite possible explanations for any of the physical processes we observe, but we are inclined to abduce a single explanation (or a few explanations) for them in the hopes that we can better orient ourselves in our surroundings and eliminate some of the possibilities.
. For example, after glancing up and seeing the eight ball moving towards us we may abduce that it was struck by the cue ball. The cue ball's strike would account for the eight ball's movement. It serves as a hypothesis that explains our observation. There are in fact infinitely many possible explanations for the eight ball's movement, and so our abduction does not leave us certain that the cue ball did in fact strike the eight ball, but our abduction is still useful and can serve to orient us in our surroundings. This process of abduction is an instance of the scientific method. There are infinite possible explanations for any of the physical processes we observe, but we are inclined to abduce a single explanation (or a few explanations) for them in the hopes that we can better orient ourselves in our surroundings and eliminate some of the possibilities.
, explanation
is done from a logical theory representing a domain
representing a domain
and a set of observations . Abduction is the process of deriving a set of explanations of
. Abduction is the process of deriving a set of explanations of  according to
according to  and picking out one of those explanations. For
and picking out one of those explanations. For  to be an explanation of
to be an explanation of  according to
according to  , it should satisfy two conditions:
, it should satisfy two conditions:
In formal logic, and
and  are assumed to be sets of literals. The two conditions for
are assumed to be sets of literals. The two conditions for  being an explanation of
being an explanation of  according to theory
according to theory  are formalized as:
are formalized as:
 ;
; is consistent.
is consistent.
Among the possible explanations satisfying these two conditions, some other condition of minimality is usually imposed to avoid irrelevant facts (not contributing to the entailment of
satisfying these two conditions, some other condition of minimality is usually imposed to avoid irrelevant facts (not contributing to the entailment of  ) being included in the explanations. Abduction is then the process that picks out some member of
) being included in the explanations. Abduction is then the process that picks out some member of  . Criteria for picking out a member representing "the best" explanation include the simplicity
. Criteria for picking out a member representing "the best" explanation include the simplicity
, the prior probability
, or the explanatory power of the explanation.
A proof theoretical abduction method for first order classical logic based on the sequent calculus
and a dual one, based on semantic tableaux (analytic tableaux) have been proposed (Cialdea Mayer & Pirri 1993). The methods are sound and complete and work for full first order logic, without requiring any preliminary reduction of formulae into normal forms. These methods have also been extended to modal logic
.
Abductive logic programming
is a computational framework that extends normal logic programming
with abduction. It separates the theory into two components, one of which is a normal logic program, used to generate
into two components, one of which is a normal logic program, used to generate  by means of backward reasoning, the other of which is a set of integrity constraints, used to filter the set of candidate explanations.
by means of backward reasoning, the other of which is a set of integrity constraints, used to filter the set of candidate explanations.
 and a set of manifestations
and a set of manifestations  ; they are related by the domain knowledge, represented by a function
; they are related by the domain knowledge, represented by a function  that takes as an argument a set of hypotheses and gives as a result the corresponding set of manifestations. In other words, for every subset of the hypotheses
that takes as an argument a set of hypotheses and gives as a result the corresponding set of manifestations. In other words, for every subset of the hypotheses 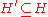 , their effects are known to be
, their effects are known to be 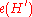 .
.
Abduction is performed by finding a set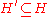 such that
such that 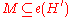 . In other words, abduction is performed by finding a set of hypotheses
. In other words, abduction is performed by finding a set of hypotheses  such that their effects
such that their effects 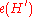 include all observations
include all observations  .
.
A common assumption is that the effects of the hypotheses are independent, that is, for every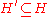 , it holds that
, it holds that 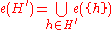 . If this condition is met, abduction can be seen as a form of set covering.
. If this condition is met, abduction can be seen as a form of set covering.
). Abductive validation is common practice in hypothesis formation in science
; moreover, Peirce argues it is a ubiquitous aspect of thought:
It was Peirce's own maxim that "Facts cannot be explained by a hypothesis more extraordinary than these facts themselves; and of various hypotheses the least extraordinary must be adopted." After obtaining results from an inference procedure, we may be left with multiple assumptions, some of which may be contradictory. Abductive validation is a method for identifying the assumptions that will lead to your goal.
 : "Positive test",
: "Positive test",  : "Negative test",
: "Negative test",  : "Infected", and
: "Infected", and 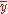 : "Not infected". The result of these trials will then determine the reliability of the test in terms of its sensitivity
: "Not infected". The result of these trials will then determine the reliability of the test in terms of its sensitivity
 and false positive rate
and false positive rate  . The interpretations of the conditionals are:
. The interpretations of the conditionals are:  : "The probability of positive test given infection", and
: "The probability of positive test given infection", and  : "The probability of positive test in the absence of infection". The problem with applying these conditionals in a practical setting is that they are expressed in the opposite direction to what the practitioner needs. The conditionals needed for making the diagnosis are:
: "The probability of positive test in the absence of infection". The problem with applying these conditionals in a practical setting is that they are expressed in the opposite direction to what the practitioner needs. The conditionals needed for making the diagnosis are: 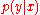 : "The probability of infection given positive test", and
: "The probability of infection given positive test", and 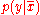 : "The probability of infection given negative test". The probability of infection could then have been conditionally deduced as
: "The probability of infection given negative test". The probability of infection could then have been conditionally deduced as 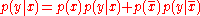 , where "" denotes conditional deduction. Unfortunately the required conditionals are usually not directly available to the medical practitioner, but they can be obtained if the base rate of the infection in the population is known.
, where "" denotes conditional deduction. Unfortunately the required conditionals are usually not directly available to the medical practitioner, but they can be obtained if the base rate of the infection in the population is known.
The required conditionals can be correctly derived by inverting the available conditionals using Bayes rule. The inverted conditionals are obtained as follows:
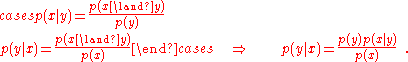
The term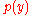 on the right hand side of the equation expresses the base rate of
on the right hand side of the equation expresses the base rate of
the infection in the population. Similarly, the term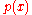 expresses the default likelihood of
expresses the default likelihood of
positive test on a random person in the population. In the expressions below
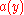 and
and 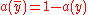 denote the base rates of
denote the base rates of 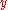 and its complement
and its complement 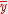 respectively, so that e.g.
respectively, so that e.g. 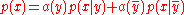 . The full expression for the required
. The full expression for the required
conditionals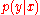 and
and 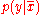 are then:
are then:

The full expression for the conditionally abduced probability of infection in a tested person, expressed as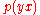 , given the outcome of the test, the base rate of the infection, as well as the test's sensitivity and false positive rate, is then given by:
, given the outcome of the test, the base rate of the infection, as well as the test's sensitivity and false positive rate, is then given by:
 .
.
Probabilistic abduction can thus be described as a method for inverting conditionals in order to apply probabilistic deduction.
A medical test result is typically considered positive or negative, so
when applying the above equation it can be assumed that
either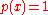 (positive) or
(positive) or 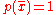 (negative). In
(negative). In
case the patient tests positive, the above equation can be
simplified to which
which
will give the correct likelihood that the patient actually is infected.
The Base rate fallacy
in medicine, or the Prosecutor's fallacy
in legal reasoning, consists of making the erroneous assumption that . While this reasoning error often can produce a relatively good approximation of the correct hypothesis probability value, it can lead to a completely wrong result and wrong conclusion in case the base rate is very low and the reliability of the test is not perfect. An extreme example of the base rate fallacy is to conclude that a male person is pregnant just because he tests positive in a pregnancy test. Obviously, the base rate of male pregnancy
. While this reasoning error often can produce a relatively good approximation of the correct hypothesis probability value, it can lead to a completely wrong result and wrong conclusion in case the base rate is very low and the reliability of the test is not perfect. An extreme example of the base rate fallacy is to conclude that a male person is pregnant just because he tests positive in a pregnancy test. Obviously, the base rate of male pregnancy
is zero, and assuming that the test is not perfect, it would be correct to conclude that the male person is not pregnant.
The expression for probabilistic abduction can be generalised to multinomial cases, i.e., with a state space of multiple
of multiple 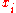 and a state space
and a state space  of multiple states
of multiple states 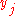 .
.
generalises probabilistic logic
by including parameters for uncertainty in the input arguments. Abduction in subjective logic is thus similar to probabilistic abduction described above. The input arguments in subjective logic are composite functions called subjective opinions which can be binomial when the opinion applies to a single proposition or multinomial when it applies to a set of propositions. A multinomial opinion thus applies to a frame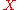 (i.e. a state space of exhaustive and mutually disjoint propositions
(i.e. a state space of exhaustive and mutually disjoint propositions 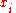 ), and is denoted by the composite
), and is denoted by the composite
function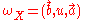 , where
, where  is a vector of belief masses over the propositions of
is a vector of belief masses over the propositions of 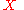 ,
,  is the uncertainty mass, and
is the uncertainty mass, and  is a vector of base rate values over the propositions of
is a vector of base rate values over the propositions of 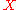 . These components satisfy
. These components satisfy 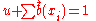 and
and 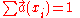 as well as
as well as 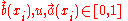 .
.
Assume the frames and
and  , the sets of conditional opinions
, the sets of conditional opinions 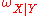 and
and 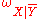 , the opinion
, the opinion 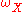 on
on  , and the base rate function
, and the base rate function  on
on  . Based on these parameters, subjective logic provides a method for deriving the set of inverted conditionals
. Based on these parameters, subjective logic provides a method for deriving the set of inverted conditionals 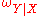 and
and 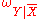 . Using these inverted conditionals, subjective logic also provides a method for deduction. Abduction in subjective logic consists of inverting the conditionals and then applying deduction.
. Using these inverted conditionals, subjective logic also provides a method for deduction. Abduction in subjective logic consists of inverting the conditionals and then applying deduction.
The symbolic notation for conditional abduction is "", and the operator itself is denoted as . The expression for subjective logic abduction is then:
. The expression for subjective logic abduction is then:
 .
.
The advantage of using subjective logic abduction compared to probabilistic abduction is that uncertainty about the probability values of the input arguments can be explicitly expressed and taken into account during the analysis. It is thus possible to perform abductive analysis in the presence of missing or incomplete input evidence, which normally results in degrees of uncertainty in the output conclusions.
As two stages of the development, extension, etc., of a hypothesis in scientific inquiry, abduction and induction
are often collapsed into one overarching concept — the hypothesis. That is why, in the scientific method
pioneered by Galileo
and Bacon
, the abductive stage of hypothesis formation is conceptualized simply as induction. In the twentieth century this collapse was reinforced by Karl Popper
's explication of the hypothetico-deductive model
, where the hypothesis is considered to be just "a guess" (in the spirit of Peirce). However, when the formation of a hypothesis is considered the result of a process it becomes clear that this "guess" has already been tried and made more robust in thought as a necessary stage of its acquiring the status of hypothesis. Indeed many abductions are rejected or heavily modified by subsequent abductions before they ever reach this stage.
Before 1900, Peirce treated abduction as the use of a known rule to explain an observation, e.g., it is a known rule that if it rains the grass is wet; so, to explain the fact that the grass is wet; one infers that it has rained. This remains the common use of the term "abduction" in the social sciences and in artificial intelligence
.
Peirce consistently characterized it as the kind of inference that originates a hypothesis by concluding in an explanation, though an unassured one, for some very curious or surprising (anomalous) observation stated in a premise. As early as 1865 he wrote that all conceptions of cause and force are reached through hypothetical inference; in the 1900s he wrote that all explanatory content of theories is reached through abduction. In other respects Peirce revised his view of abduction over the years.
In later years his view came to be:
Writing in 1910, Peirce admits that "in almost everything I printed before the beginning of this century I more or less mixed up hypothesis and induction" and he traces the confusion of these two types of reasoning to logicians' too "narrow and formalistic a conception of inference, as necessarily having formulated judgments from its premises."
He started out in the 1860s treating hypothetical inference in a number of ways which he eventually peeled away as inessential or, in some cases, mistaken:
Barbara (AAA).)
), unlike his later amendments of his conception of abduction. Today abduction remains most commonly understood as induction from characters and extension of a known rule to cover unexplained circumstances.
The hypothesis is framed, but not asserted, in a premise, then asserted as rationally suspectable in the conclusion. Thus, as in the earlier categorical syllogistic form, the conclusion is formulated from some premise(s). But all the same the hypothesis consists more clearly than ever in a new or outside idea beyond what is known or observed. Induction in a sense goes beyond observations already reported in the premises, but it merely amplifies ideas already known to represent occurrences, or tests an idea supplied by hypothesis; either way it requires previous abductions in order to get such ideas in the first place. Induction seeks facts to test a hypothesis; abduction seeks a hypothesis to account for facts.
Note that the hypothesis ("A") could be of a rule. It need not even be a rule strictly necessitating the surprising observation ("C"), which needs to follow only as a "matter of course"; or the "course" itself could amount to some known rule, merely alluded to, and also not necessarily a rule of strict necessity. In the same year, Peirce wrote that reaching a hypothesis may involve placing a surprising observation under either a newly hypothesized rule or a hypothesized combination of a known rule with a peculiar state of facts, so that the phenomenon would be not surprising but instead either necessarily implied or at least likely.
Peirce did not remain quite convinced about any such form as the categorical syllogistic form or the 1903 form. In 1911, he wrote, "I do not, at present, feel quite convinced that any logical form can be assigned that will cover all "Retroductions". For what I mean by a Retroduction is simply a conjecture which arises in the mind."
Peirce had, from the start, seen the modes of inference as being coordinated together in scientific inquiry and, by the 1900s, held that hypothetical inference in particular is inadequately treated at the level of critique of arguments. To increase the assurance of a hypothetical conclusion, one needs to deduce implications about evidence to be found, predictions which induction can test through observation so as to evaluate the hypothesis. That is Peirce's outline of the scientific method of inquiry, as covered in his inquiry methodology, which includes pragmatism
or, as he later called it, pragmaticism
, the clarification of ideas in terms of their conceivable implications regarding informed practice.
1. Hypothesis (abductive inference) is inference through an icon (also called a likeness).
2. Induction is inference through an index (a sign by factual connection); a sample is an index of the totality from which it is drawn.
3. Deduction is inference through a symbol (a sign by interpretive habit irrespective of resemblance or connection to its object).
In 1902, Peirce wrote that, in abduction: "It is recognized that the phenomena are like, i.e. constitute an Icon of, a replica of a general conception, or Symbol."
The phrase "inference to the best explanation" (not used by Peirce but often applied to hypothetical inference) is not always understood as referring to the most simple and natural. However, in other senses of "best", such as "standing up best to tests", it is hard to know which is the best explanation to form, since one has not tested it yet.
In 1901 Peirce wrote, "There would be no logic in imposing rules, and saying that they ought to be followed, until it is made out that the purpose of hypothesis requires them." In 1903 Peirce called pragmatism
"the logic of abduction" and said that the pragmatic maxim
gives the necessary and sufficient logical rule to abduction in general. The pragmatic maxim is: "Consider what effects, that might conceivably have practical bearings, we conceive the object of our conception to have. Then, our conception of these effects is the whole of our conception of the object." It is a method for fruitful clarification of conceptions by equating the meaning of a conception with the conceivable practical implications of its object's conceived effects. Peirce held that that is precisely tailored to abduction's purpose in inquiry, the forming of an idea that could conceivably shape informed conduct. In various writings in the 1900s he said that the conduct of abduction (or retroduction) is governed by considerations of economy, belonging in particular to the economics of research. He regarded economics as a normative science whose analytic portion might be part of logical methodeutic.
, a philosopher of science, wanted to grasp a logic explaining how scientific discoveries take place. He used Peirce's notion of abduction for this.
Further development of the concept can be found in Peter Lipton
's Inference to the Best Explanation (Lipton, 1991).
include fault diagnosis
, belief revision
, and automated planning. The most direct application of abduction is that of automatically detecting faults in systems: given a theory relating faults with their effects and a set of observed effects, abduction can be used to derive sets of faults that are likely to be the cause of the problem.
Abduction can also be used to model automated planning. Given a logical theory relating action occurrences with their effects (for example, a formula of the event calculus
), the problem of finding a plan for reaching a state can be modeled as the problem of abducting a set of literals implying that the final state is the goal state.
In intelligence analysis
, Analysis of Competing Hypotheses
and Bayesian network
s, probabilistic abductive reasoning is used extensively. Similarly in medical diagnosis
and legal reasoning, the same methods are being used, although there have been many examples of errors, especially caused by the base rate fallacy
and the prosecutor's fallacy
.
Belief revision
, the process of adapting beliefs in view of new information, is another field in which abduction has been applied. The main problem of belief revision is that the new information may be inconsistent with the corpus of beliefs, while the result of the incorporation cannot be inconsistent. This process can be done by the use of abduction: once an explanation for the observation has been found, integrating it does not generate inconsistency. This use of abduction is not straightforward, as adding propositional formula
e to other propositional formulae can only make inconsistencies worse. Instead, abduction is done at the level of the ordering of preference of the possible worlds. Preference models use fuzzy logic or utility models.
In the philosophy of science
, abduction has been the key inference method to support scientific realism
, and much of the debate about scientific realism is focused on whether abduction is an acceptable method of inference.
In historical linguistics
, abduction during language acquisition is often taken to be an essential part of processes of language change
such as reanalysis and analogy
.
In anthropology
, Alfred Gell
in his influential book Art and Agency defined abduction, (after Eco) as “a case of synthetic inference 'where we find some very curious circumstances, which would be explained by the supposition that it was a case of some general rule, and thereupon adopt that supposition”. Gell criticizes existing 'anthropological' studies of art, for being too preoccupied with aesthetic value and not preoccupied enough with the central anthropological concern of uncovering 'social relationships' specifically the social contexts in which artworks are produced, circulated, and received. Abduction is used as the basis of one gets from art to agency in the sense of a theory of how works of art can inspire a sensus communis, or the commonly-held views that a characteristic of a given society because they are shared by everyone in that society. The question Gell asks in the book is, ‘how does initially to ‘speak’ to people?’ He answers by saying that “No reasonable person could suppose that art-like relations between people and things do not involve at least some form of semiosis
.” However, he rejects any intimation that semiosis can be thought of as a language because then he would have to admit to some pre-established existence of the sensus communis that he wants to claim only emerges afterward out of art. Abduction is the answer to this conundrum because the tentative nature of the abduction concept (Pierce likened it to guessing) means that not only can it operate outside of any pre-existing framework, but moreover, it can actually intimate the existence of a framework. As Gell reasons in his analysis, the physical existence of the artwork prompts the viewer to perform an abduction that imbues the artwork with intentionality. A statue of a goddess, for example, in some senses actually becomes the goddess in the mind of the beholder; and represents not only the form of the deity but also her intentions (which are adduced from the feeling of her very presence). Therefore through abduction, Gell claims that art can have the kind of agency that plants the seeds that grow into cultural myths. The power of agency is the power to motivate actions and inspire ultimately the shared understanding that characterizes any given society.
 from an observed surprising circumstance
from an observed surprising circumstance  is to surmise that
is to surmise that  may be true because then
may be true because then  would be a matter of course. Thus, to abduce
would be a matter of course. Thus, to abduce  from
from  involves determining that
involves determining that  is sufficient (or nearly sufficient), but not necessary
is sufficient (or nearly sufficient), but not necessaryNecessary and sufficient conditions
In logic, the words necessity and sufficiency refer to the implicational relationships between statements. The assertion that one statement is a necessary and sufficient condition of another means that the former statement is true if and only if the latter is true.-Definitions:A necessary condition...
, for
 .
.For example, the lawn is wet. But if it rained last night, then it would be unsurprising that the lawn is wet. Therefore, by abductive reasoning, the possibility that it rained last night is reasonable. (But note that Peirce did not remain convinced that a single logical form covers all abduction.)
Peirce argues that good abductive reasoning from P to Q involves not simply a determination that, e.g., Q is sufficient for P, but also that Q is among the most economical explanation
Explanatory power
Explanatory power is the ability of a theory to effectively explain the subject matter it pertains to. One theory is sometimes said to have more explanatory power than another theory about the same subject matter if it offers greater predictive power...
s for P. Simplification and economy are what call for the 'leap' of abduction.
There has been renewed interest in the subject of abduction in the fields of computer science and artificial intelligence research.
Deduction, induction, and abduction
DeductionDeductive reasoning
Deductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
: allows deriving
 from
from  only where
only where  is a formal consequence of
is a formal consequence of  . In other words, deduction is the process of deriving the consequences of what is assumed. Given the truth of the assumptions, a valid deduction guarantees the truth of the conclusion. For example, given that all bachelors are unmarried males, and given that this person is a bachelor, it can be deduced that this person is an unmarried male.
. In other words, deduction is the process of deriving the consequences of what is assumed. Given the truth of the assumptions, a valid deduction guarantees the truth of the conclusion. For example, given that all bachelors are unmarried males, and given that this person is a bachelor, it can be deduced that this person is an unmarried male.Induction
Inductive reasoning
Inductive reasoning, also known as induction or inductive logic, is a kind of reasoning that constructs or evaluates propositions that are abstractions of observations. It is commonly construed as a form of reasoning that makes generalizations based on individual instances...
: allows inferring
 from
from  , where
, where  does not follow necessarily from
does not follow necessarily from  .
.  might give us very good reason to accept
might give us very good reason to accept  , but it does not ensure that
, but it does not ensure that  . For example, if all of the swans that we have observed so far are white, we may induce that the possibility that all swans are white is reasonable. We have good reason to believe the conclusion from the premise, but the truth of the conclusion is not guaranteed. (Indeed, it turns out that some swans are black
. For example, if all of the swans that we have observed so far are white, we may induce that the possibility that all swans are white is reasonable. We have good reason to believe the conclusion from the premise, but the truth of the conclusion is not guaranteed. (Indeed, it turns out that some swans are blackBlack swan theory
The black swan theory or theory of black swan events is a metaphor that encapsulates the concept that The event is a surprise and has a major impact...
.)
Abduction : allows inferring
 as an explanation of
as an explanation of  . Because of this, abduction allows the precondition
. Because of this, abduction allows the precondition  to be abduced from the consequence
to be abduced from the consequence  . Deduction
. DeductionDeductive reasoning
Deductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
and abduction thus differ in the direction in which a rule like "
 entail
entailEntailment
In logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
s
 " is used for inference. As such abduction is formally equivalent to the logical fallacy affirming the consequent
" is used for inference. As such abduction is formally equivalent to the logical fallacy affirming the consequentAffirming the consequent
Affirming the consequent, sometimes called converse error, is a formal fallacy, committed by reasoning in the form:#If P, then Q.#Q.#Therefore, P....
or Post hoc ergo propter hoc
Post hoc ergo propter hoc
Post hoc ergo propter hoc, Latin for "after this, therefore because of this," is a logical fallacy that states, "Since that event followed this one, that event must have been caused by this one." It is often shortened to simply post hoc and is also sometimes referred to as false cause,...
, because there are multiple possible explanations for
 . For example, after glancing up and seeing the eight ball moving towards us we may abduce that it was struck by the cue ball. The cue ball's strike would account for the eight ball's movement. It serves as a hypothesis that explains our observation. There are in fact infinitely many possible explanations for the eight ball's movement, and so our abduction does not leave us certain that the cue ball did in fact strike the eight ball, but our abduction is still useful and can serve to orient us in our surroundings. This process of abduction is an instance of the scientific method. There are infinite possible explanations for any of the physical processes we observe, but we are inclined to abduce a single explanation (or a few explanations) for them in the hopes that we can better orient ourselves in our surroundings and eliminate some of the possibilities.
. For example, after glancing up and seeing the eight ball moving towards us we may abduce that it was struck by the cue ball. The cue ball's strike would account for the eight ball's movement. It serves as a hypothesis that explains our observation. There are in fact infinitely many possible explanations for the eight ball's movement, and so our abduction does not leave us certain that the cue ball did in fact strike the eight ball, but our abduction is still useful and can serve to orient us in our surroundings. This process of abduction is an instance of the scientific method. There are infinite possible explanations for any of the physical processes we observe, but we are inclined to abduce a single explanation (or a few explanations) for them in the hopes that we can better orient ourselves in our surroundings and eliminate some of the possibilities.Logic-based abduction
In logicLogic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, explanation
Explanation
An explanation is a set of statements constructed to describe a set of facts which clarifies the causes, context, and consequencesof those facts....
is done from a logical theory
 representing a domain
representing a domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
and a set of observations
 . Abduction is the process of deriving a set of explanations of
. Abduction is the process of deriving a set of explanations of  according to
according to  and picking out one of those explanations. For
and picking out one of those explanations. For  to be an explanation of
to be an explanation of  according to
according to  , it should satisfy two conditions:
, it should satisfy two conditions:-
 follows from
follows from  and
and  ;
;
-
 is consistent with
is consistent with  .
.
In formal logic,
 and
and  are assumed to be sets of literals. The two conditions for
are assumed to be sets of literals. The two conditions for  being an explanation of
being an explanation of  according to theory
according to theory  are formalized as:
are formalized as: ;
; is consistent.
is consistent.Among the possible explanations
 satisfying these two conditions, some other condition of minimality is usually imposed to avoid irrelevant facts (not contributing to the entailment of
satisfying these two conditions, some other condition of minimality is usually imposed to avoid irrelevant facts (not contributing to the entailment of  ) being included in the explanations. Abduction is then the process that picks out some member of
) being included in the explanations. Abduction is then the process that picks out some member of  . Criteria for picking out a member representing "the best" explanation include the simplicity
. Criteria for picking out a member representing "the best" explanation include the simplicitySimplicity
Simplicity is the state or quality of being simple. It usually relates to the burden which a thing puts on someone trying to explain or understand it. Something which is easy to understand or explain is simple, in contrast to something complicated...
, the prior probability
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
, or the explanatory power of the explanation.
A proof theoretical abduction method for first order classical logic based on the sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
and a dual one, based on semantic tableaux (analytic tableaux) have been proposed (Cialdea Mayer & Pirri 1993). The methods are sound and complete and work for full first order logic, without requiring any preliminary reduction of formulae into normal forms. These methods have also been extended to modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
.
Abductive logic programming
Abductive logic programming
Abductive logic programming is a high level knowledge-representation framework that can be used to solve problems declaratively based on abductive reasoning. It extends normal logic programming by allowing some predicates to be incompletely defined, declared as abducible predicates...
is a computational framework that extends normal logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
with abduction. It separates the theory
 into two components, one of which is a normal logic program, used to generate
into two components, one of which is a normal logic program, used to generate  by means of backward reasoning, the other of which is a set of integrity constraints, used to filter the set of candidate explanations.
by means of backward reasoning, the other of which is a set of integrity constraints, used to filter the set of candidate explanations.Set-cover abduction
A different formalization of abduction is based on inverting the function that calculates the visible effects of the hypotheses. Formally, we are given a set of hypotheses and a set of manifestations
and a set of manifestations  ; they are related by the domain knowledge, represented by a function
; they are related by the domain knowledge, represented by a function  that takes as an argument a set of hypotheses and gives as a result the corresponding set of manifestations. In other words, for every subset of the hypotheses
that takes as an argument a set of hypotheses and gives as a result the corresponding set of manifestations. In other words, for every subset of the hypotheses 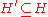 , their effects are known to be
, their effects are known to be 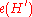 .
.Abduction is performed by finding a set
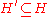 such that
such that 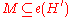 . In other words, abduction is performed by finding a set of hypotheses
. In other words, abduction is performed by finding a set of hypotheses  such that their effects
such that their effects 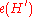 include all observations
include all observations  .
.A common assumption is that the effects of the hypotheses are independent, that is, for every
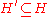 , it holds that
, it holds that 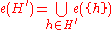 . If this condition is met, abduction can be seen as a form of set covering.
. If this condition is met, abduction can be seen as a form of set covering.Abductive validation
Abductive validation is the process of validating a given hypothesis through abductive reasoning. This can also be called reasoning through successive approximation. Under this principle, an explanation is valid if it is the best possible explanation of a set of known data. The best possible explanation is often defined in terms of simplicity and elegance (see Occam's razorOccam's razor
Occam's razor, also known as Ockham's razor, and sometimes expressed in Latin as lex parsimoniae , is a principle that generally recommends from among competing hypotheses selecting the one that makes the fewest new assumptions.-Overview:The principle is often summarized as "simpler explanations...
). Abductive validation is common practice in hypothesis formation in science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
; moreover, Peirce argues it is a ubiquitous aspect of thought:
Looking out my window this lovely spring morning I see an azalea in full bloom. No, no! I do not see that; though that is the only way I can describe what I see. That is a proposition, a sentence, a fact; but what I perceive is not proposition, sentence, fact, but only an image, which I make intelligible in part by means of a statement of fact. This statement is abstract; but what I see is concrete. I perform an abduction when I so much as express in a sentence anything I see. The truth is that the whole fabric of our knowledge is one matted felt of pure hypothesis confirmed and refined by induction. Not the smallest advance can be made in knowledge beyond the stage of vacant staring, without making an abduction at every step.
It was Peirce's own maxim that "Facts cannot be explained by a hypothesis more extraordinary than these facts themselves; and of various hypotheses the least extraordinary must be adopted." After obtaining results from an inference procedure, we may be left with multiple assumptions, some of which may be contradictory. Abductive validation is a method for identifying the assumptions that will lead to your goal.
Probabilistic abduction
Probabilistic abductive reasoning is a form of abductive validation, and is used extensively in areas where conclusions about possible hypotheses need to be derived, such as for making diagnoses from medical tests. For example, a pharmaceutical company that develops a test for a particular infectious disease will typically determine the reliability of the test by letting a group of infected and a group of non-infected people undergo the test. Assume the statements : "Positive test",
: "Positive test",  : "Negative test",
: "Negative test",  : "Infected", and
: "Infected", and 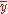 : "Not infected". The result of these trials will then determine the reliability of the test in terms of its sensitivity
: "Not infected". The result of these trials will then determine the reliability of the test in terms of its sensitivitySensitivity and specificity
Sensitivity and specificity are statistical measures of the performance of a binary classification test, also known in statistics as classification function. Sensitivity measures the proportion of actual positives which are correctly identified as such Sensitivity and specificity are statistical...
 and false positive rate
and false positive rate  . The interpretations of the conditionals are:
. The interpretations of the conditionals are:  : "The probability of positive test given infection", and
: "The probability of positive test given infection", and  : "The probability of positive test in the absence of infection". The problem with applying these conditionals in a practical setting is that they are expressed in the opposite direction to what the practitioner needs. The conditionals needed for making the diagnosis are:
: "The probability of positive test in the absence of infection". The problem with applying these conditionals in a practical setting is that they are expressed in the opposite direction to what the practitioner needs. The conditionals needed for making the diagnosis are: 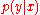 : "The probability of infection given positive test", and
: "The probability of infection given positive test", and 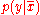 : "The probability of infection given negative test". The probability of infection could then have been conditionally deduced as
: "The probability of infection given negative test". The probability of infection could then have been conditionally deduced as 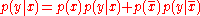 , where "" denotes conditional deduction. Unfortunately the required conditionals are usually not directly available to the medical practitioner, but they can be obtained if the base rate of the infection in the population is known.
, where "" denotes conditional deduction. Unfortunately the required conditionals are usually not directly available to the medical practitioner, but they can be obtained if the base rate of the infection in the population is known.The required conditionals can be correctly derived by inverting the available conditionals using Bayes rule. The inverted conditionals are obtained as follows:
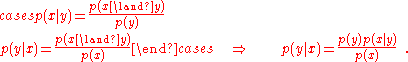
The term
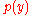 on the right hand side of the equation expresses the base rate of
on the right hand side of the equation expresses the base rate ofthe infection in the population. Similarly, the term
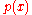 expresses the default likelihood of
expresses the default likelihood ofpositive test on a random person in the population. In the expressions below
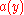 and
and 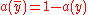 denote the base rates of
denote the base rates of 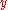 and its complement
and its complement 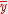 respectively, so that e.g.
respectively, so that e.g. 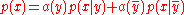 . The full expression for the required
. The full expression for the requiredconditionals
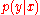 and
and 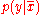 are then:
are then:
The full expression for the conditionally abduced probability of infection in a tested person, expressed as
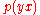 , given the outcome of the test, the base rate of the infection, as well as the test's sensitivity and false positive rate, is then given by:
, given the outcome of the test, the base rate of the infection, as well as the test's sensitivity and false positive rate, is then given by: .
.Probabilistic abduction can thus be described as a method for inverting conditionals in order to apply probabilistic deduction.
A medical test result is typically considered positive or negative, so
when applying the above equation it can be assumed that
either
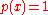 (positive) or
(positive) or 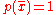 (negative). In
(negative). Incase the patient tests positive, the above equation can be
simplified to
 which
whichwill give the correct likelihood that the patient actually is infected.
The Base rate fallacy
Base rate fallacy
The base rate fallacy, also called base rate neglect or base rate bias, is an error that occurs when the conditional probability of some hypothesis H given some evidence E is assessed without taking into account the "base rate" or "prior probability" of H and the total probability of evidence...
in medicine, or the Prosecutor's fallacy
Prosecutor's fallacy
The prosecutor's fallacy is a fallacy of statistical reasoning made in law where the context in which the accused has been brought to court is falsely assumed to be irrelevant to judging how confident a jury can be in evidence against them with a statistical measure of doubt...
in legal reasoning, consists of making the erroneous assumption that
 . While this reasoning error often can produce a relatively good approximation of the correct hypothesis probability value, it can lead to a completely wrong result and wrong conclusion in case the base rate is very low and the reliability of the test is not perfect. An extreme example of the base rate fallacy is to conclude that a male person is pregnant just because he tests positive in a pregnancy test. Obviously, the base rate of male pregnancy
. While this reasoning error often can produce a relatively good approximation of the correct hypothesis probability value, it can lead to a completely wrong result and wrong conclusion in case the base rate is very low and the reliability of the test is not perfect. An extreme example of the base rate fallacy is to conclude that a male person is pregnant just because he tests positive in a pregnancy test. Obviously, the base rate of male pregnancyMale pregnancy
Male pregnancy refers to the incubation of one or more embryos or fetuses by male members of any species. In nearly all heterogamous animal species, offspring are ordinarily carried by the female until birth, but in fish of the Syngnathidae family , males perform this function...
is zero, and assuming that the test is not perfect, it would be correct to conclude that the male person is not pregnant.
The expression for probabilistic abduction can be generalised to multinomial cases, i.e., with a state space
 of multiple
of multiple 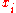 and a state space
and a state space  of multiple states
of multiple states 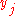 .
.Subjective logic abduction
Subjective logicSubjective logic
Subjective logic is a type of probabilistic logic that explicitly takes uncertainty and belief ownership into account. In general, subjective logic is suitable for modeling and analysing situations involving uncertainty and incomplete knowledge...
generalises probabilistic logic
Probabilistic logic
The aim of a probabilistic logic is to combine the capacity of probability theory to handle uncertainty with the capacity of deductive logic to exploit structure. The result is a richer and more expressive formalism with a broad range of possible application areas...
by including parameters for uncertainty in the input arguments. Abduction in subjective logic is thus similar to probabilistic abduction described above. The input arguments in subjective logic are composite functions called subjective opinions which can be binomial when the opinion applies to a single proposition or multinomial when it applies to a set of propositions. A multinomial opinion thus applies to a frame
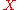 (i.e. a state space of exhaustive and mutually disjoint propositions
(i.e. a state space of exhaustive and mutually disjoint propositions 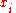 ), and is denoted by the composite
), and is denoted by the compositefunction
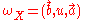 , where
, where  is a vector of belief masses over the propositions of
is a vector of belief masses over the propositions of 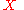 ,
,  is the uncertainty mass, and
is the uncertainty mass, and  is a vector of base rate values over the propositions of
is a vector of base rate values over the propositions of 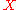 . These components satisfy
. These components satisfy 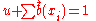 and
and 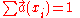 as well as
as well as 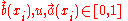 .
.Assume the frames
 and
and  , the sets of conditional opinions
, the sets of conditional opinions 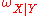 and
and 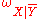 , the opinion
, the opinion 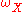 on
on  , and the base rate function
, and the base rate function  on
on  . Based on these parameters, subjective logic provides a method for deriving the set of inverted conditionals
. Based on these parameters, subjective logic provides a method for deriving the set of inverted conditionals 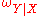 and
and 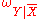 . Using these inverted conditionals, subjective logic also provides a method for deduction. Abduction in subjective logic consists of inverting the conditionals and then applying deduction.
. Using these inverted conditionals, subjective logic also provides a method for deduction. Abduction in subjective logic consists of inverting the conditionals and then applying deduction.The symbolic notation for conditional abduction is "", and the operator itself is denoted as
 . The expression for subjective logic abduction is then:
. The expression for subjective logic abduction is then: .
.The advantage of using subjective logic abduction compared to probabilistic abduction is that uncertainty about the probability values of the input arguments can be explicitly expressed and taken into account during the analysis. It is thus possible to perform abductive analysis in the presence of missing or incomplete input evidence, which normally results in degrees of uncertainty in the output conclusions.
History of the concept
The philosopher Charles Sanders Peirce (icon; 1839–1914) introduced abduction into modern logic. Over the years he called such inference hypothesis, abduction, presumption, and retroduction. He considered it a topic in logic as a normative field in philosophy, not in purely formal or mathematical logic, and eventually as a topic also in economics of research.As two stages of the development, extension, etc., of a hypothesis in scientific inquiry, abduction and induction
Inductive reasoning
Inductive reasoning, also known as induction or inductive logic, is a kind of reasoning that constructs or evaluates propositions that are abstractions of observations. It is commonly construed as a form of reasoning that makes generalizations based on individual instances...
are often collapsed into one overarching concept — the hypothesis. That is why, in the scientific method
Scientific method
Scientific method refers to a body of techniques for investigating phenomena, acquiring new knowledge, or correcting and integrating previous knowledge. To be termed scientific, a method of inquiry must be based on gathering empirical and measurable evidence subject to specific principles of...
pioneered by Galileo
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
and Bacon
Francis Bacon
Francis Bacon, 1st Viscount St Albans, KC was an English philosopher, statesman, scientist, lawyer, jurist, author and pioneer of the scientific method. He served both as Attorney General and Lord Chancellor of England...
, the abductive stage of hypothesis formation is conceptualized simply as induction. In the twentieth century this collapse was reinforced by Karl Popper
Karl Popper
Sir Karl Raimund Popper, CH FRS FBA was an Austro-British philosopher and a professor at the London School of Economics...
's explication of the hypothetico-deductive model
Hypothetico-deductive model
The hypothetico-deductive model or method, first so-named by William Whewell, is a proposed description of scientific method. According to it, scientific inquiry proceeds by formulating a hypothesis in a form that could conceivably be falsified by a test on observable data...
, where the hypothesis is considered to be just "a guess" (in the spirit of Peirce). However, when the formation of a hypothesis is considered the result of a process it becomes clear that this "guess" has already been tried and made more robust in thought as a necessary stage of its acquiring the status of hypothesis. Indeed many abductions are rejected or heavily modified by subsequent abductions before they ever reach this stage.
Before 1900, Peirce treated abduction as the use of a known rule to explain an observation, e.g., it is a known rule that if it rains the grass is wet; so, to explain the fact that the grass is wet; one infers that it has rained. This remains the common use of the term "abduction" in the social sciences and in artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
.
Peirce consistently characterized it as the kind of inference that originates a hypothesis by concluding in an explanation, though an unassured one, for some very curious or surprising (anomalous) observation stated in a premise. As early as 1865 he wrote that all conceptions of cause and force are reached through hypothetical inference; in the 1900s he wrote that all explanatory content of theories is reached through abduction. In other respects Peirce revised his view of abduction over the years.
In later years his view came to be:
- Abduction is guessing. It is "very little hampered" by rules of logic. Even a well-prepared mind's individual guesses are oftener wrong than right. But the success of our guesses far exceeds that of random luck and seems born of attunement to nature by instinct (some speak of intuition in such contexts).
- Abduction guesses a new or outside idea so as to account in a plausible, instinctive, economical way for a surprising or very complicated phenomenon. That is its proximate aim.
- Its longer aim is to economize inquiry itself. Its rationale is inductive: it works often enough, is the only source of new ideas, and has no substitute in expediting the discovery of new truths. Its rationale especially involves its role in coordination with other modes of inference in inquiry. It is inference to explanatory hypotheses for selection of those best worth trying.
- PragmatismPragmatismPragmatism is a philosophical tradition centered on the linking of practice and theory. It describes a process where theory is extracted from practice, and applied back to practice to form what is called intelligent practice...
is the logic of abduction. Upon the generation of an explanation (which he came to regard as instinctively guided), the pragmatic maximPragmatic maximThe pragmatic maxim, also known as the maxim of pragmatism or the maxim of pragmaticism, is a maxim of logic formulated by Charles Sanders Peirce...
gives the necessary and sufficient logical rule to abduction in general. The hypothesis, being insecure, needs to have conceivable implications for informed practice, so as to be testable and, through its trials, to expedite and economize inquiry. The economy of research is what calls for abduction and governs its art.
Writing in 1910, Peirce admits that "in almost everything I printed before the beginning of this century I more or less mixed up hypothesis and induction" and he traces the confusion of these two types of reasoning to logicians' too "narrow and formalistic a conception of inference, as necessarily having formulated judgments from its premises."
He started out in the 1860s treating hypothetical inference in a number of ways which he eventually peeled away as inessential or, in some cases, mistaken:
- as inferring the occurrence of a character (a characteristic) from the observed combined occurrence of multiple characters which its occurrence would necessarily involve (but by 1878 he no longer regarded such multiplicity as common to all hypothetical inference.)
- as aiming for a more or less probable hypothesis (in 1867 and 1883 but not in 1878; anyway by 1900 the justification is not probability but the lack of alternatives to guessing and the fact that guessing is fruitful.; by 1903 he speaks of the "likely" in the sense of nearing the truth in an "indefinite sense"; by 1908 he discusses plausibility as instinctive appeal.)
- as induction from characters (but as early as 1900 he characterized abduction as guessing)
- as citing a known rule in a premise rather than hypothesizing a rule in the conclusion (but by 1903 he allowed either approach)
- as basically a transformation of a deductive categorical syllogism (but in 1903 he offered a variation on modus ponens instead, and by 1911 he was unconvinced that any one form covers all hypothetical inference).
1867
In 1867, in "The Natural Classification of Arguments", hypothetical inference always deals with a cluster of characters (call them P′, P′′, P′′′, etc.) known to occur at least whenever a certain character (M) occurs. (Note that categorical syllogisms have elements traditionally called middles, predicates, and subjects. For example: All men [middle] are mortal [predicate]; Socrates [subject] is a man [middle]; ergo Socrates [subject] is mortal [predicate]". Below, 'M' stands for a middle; 'P' for a predicate; 'S' for a subject. Note also that Peirce held that all deduction can be put into the form of the categorical syllogismSyllogism
A syllogism is a kind of logical argument in which one proposition is inferred from two or more others of a certain form...
Barbara (AAA).)
| [Deduction]. [Any] M is P [Any] S is M  [Any] S is P. [Any] S is P. |
Induction. S′, S′′, S′′′, &c. are taken at random as Ms; S′, S′′, S′′′, &c. are P:  Any M is probably P. Any M is probably P. |
Hypothesis. Any M is, for instance, P′, P′′, P′′′, &c.; S is P′, P′′, P′′′, &c.:  S is probably M. S is probably M. |
1878
In 1878, in "Deduction, Induction, and Hypothesis", there is no longer a need for multiple characters or predicates in order for an inference to be hypothetical, although it is still helpful. Moreover Peirce no longer poses hypothetical inference as concluding in a probable hypothesis. In the forms themselves, it is understood but not explicit that induction involves random selection and that hypothetical inference involves response to a "very curious circumstance". The forms instead emphasize the modes of inference as rearrangements of one another's propositions (without the bracketed hints shown below).| Deduction. Rule: All the beans from this bag are white. Case: These beans are from this bag.  Result: These beans are white. Result: These beans are white. |
Induction. Case: These beans are [randomly selected] from this bag. Result: These beans are white.  Rule: All the beans from this bag are white. Rule: All the beans from this bag are white. |
Hypothesis. Rule: All the beans from this bag are white. Result: These beans [oddly] are white.  Case: These beans are from this bag. Case: These beans are from this bag. |
1883
Peirce long treated abduction in terms of induction from characters or traits (weighed, not counted like objects), explicitly so in his influential 1883 "A Theory of Probable Inference", in which he returns to involving probability in the hypothetical conclusion. Like "Deduction, Induction, and Hypothesis" in 1878, it was widely read (see the historical books on statistics by Stephen StiglerStephen Stigler
Stephen Mack Stigler is Ernest DeWitt Burton Distinguished Service Professor at the Department of Statistics of the University of Chicago. His research has focused on statistical theory of robust estimators and the history of statistics...
), unlike his later amendments of his conception of abduction. Today abduction remains most commonly understood as induction from characters and extension of a known rule to cover unexplained circumstances.
1902 and after
In 1902 Peirce wrote that he now regarded the syllogistical forms and the doctrine of extension and comprehension (i.e., objects and characters as referenced by terms), as being less fundamental than he had earlier thought. In 1903 he offered the following form for abduction:The hypothesis is framed, but not asserted, in a premise, then asserted as rationally suspectable in the conclusion. Thus, as in the earlier categorical syllogistic form, the conclusion is formulated from some premise(s). But all the same the hypothesis consists more clearly than ever in a new or outside idea beyond what is known or observed. Induction in a sense goes beyond observations already reported in the premises, but it merely amplifies ideas already known to represent occurrences, or tests an idea supplied by hypothesis; either way it requires previous abductions in order to get such ideas in the first place. Induction seeks facts to test a hypothesis; abduction seeks a hypothesis to account for facts.
Note that the hypothesis ("A") could be of a rule. It need not even be a rule strictly necessitating the surprising observation ("C"), which needs to follow only as a "matter of course"; or the "course" itself could amount to some known rule, merely alluded to, and also not necessarily a rule of strict necessity. In the same year, Peirce wrote that reaching a hypothesis may involve placing a surprising observation under either a newly hypothesized rule or a hypothesized combination of a known rule with a peculiar state of facts, so that the phenomenon would be not surprising but instead either necessarily implied or at least likely.
Peirce did not remain quite convinced about any such form as the categorical syllogistic form or the 1903 form. In 1911, he wrote, "I do not, at present, feel quite convinced that any logical form can be assigned that will cover all "Retroductions". For what I mean by a Retroduction is simply a conjecture which arises in the mind."
Three levels of logic about abduction
Peirce came over the years to divide (philosophical) logic into three departments:- Stechiology or speculative grammar, on the conditions for meaningfulness. Classification of signs (semblances, symptoms, symbols, etc.) and their combinations (as well as their objects and interpretantInterpretantAn interpretant, in semiotics, is the effect of a sign on someone who reads or comprehends it. The concept of "interpretant" is part of Charles Sanders Peirce's "triadic" theory of the sign...
s). - Logical critic, on validity or justifiability of inference, the conditions for true representation. Critique of arguments in their various modes (deduction, induction, abduction).
- Methodeutic or speculative rhetoric, on the conditions for determination of interpretations. Methodology of inquiry in its mutually interacting modes.
Peirce had, from the start, seen the modes of inference as being coordinated together in scientific inquiry and, by the 1900s, held that hypothetical inference in particular is inadequately treated at the level of critique of arguments. To increase the assurance of a hypothetical conclusion, one needs to deduce implications about evidence to be found, predictions which induction can test through observation so as to evaluate the hypothesis. That is Peirce's outline of the scientific method of inquiry, as covered in his inquiry methodology, which includes pragmatism
Pragmatism
Pragmatism is a philosophical tradition centered on the linking of practice and theory. It describes a process where theory is extracted from practice, and applied back to practice to form what is called intelligent practice...
or, as he later called it, pragmaticism
Pragmaticism
Pragmaticism is a term used by Charles Sanders Peirce for his pragmatic philosophy starting in 1905, in order to distance himself and it from pragmatism, the original name, which had been used in a manner he did not approve of in the "literary journals"...
, the clarification of ideas in terms of their conceivable implications regarding informed practice.
Classification of signs
As early as 1866, Peirce held that:1. Hypothesis (abductive inference) is inference through an icon (also called a likeness).
2. Induction is inference through an index (a sign by factual connection); a sample is an index of the totality from which it is drawn.
3. Deduction is inference through a symbol (a sign by interpretive habit irrespective of resemblance or connection to its object).
In 1902, Peirce wrote that, in abduction: "It is recognized that the phenomena are like, i.e. constitute an Icon of, a replica of a general conception, or Symbol."
Critique of arguments
At the critical level Peirce held that the hypothesis should economize explanation for plausibility in terms of the feasible and natural. In 1908 Peirce described this plausibility in some detail. It involves not likeliness based on observations (which is instead the inductive evaluation of a hypothesis), but instead optimal simplicity in the sense of the "facile and natural", as by Galileo's natural light of reason and as distinct from "logical simplicity" (Peirce does not dismiss logical simplicity entirely but sees it in a subordinate role; taken to its logical extreme it would favor adding no explanation to the observation at all). Even a well-prepared mind guesses oftener wrong than right, but our guesses succeed better than random luck at reaching the truth or at least advancing the inquiry, and that indicates to Peirce that they are based in instinctive attunement to nature, an affinity between the mind's processes and the processes of the real, which would account for why appealingly "natural" guesses are the ones that oftenest (or least seldom) succeed; to which Peirce added the argument that such guesses are to be preferred since, without "a natural bent like nature's", people would have no hope of understanding nature. In 1910 Peirce made a three-way distinction between probability, verisimilitude, and plausibility, and defined plausibility with a normative "ought": "By plausibility, I mean the degree to which a theory ought to recommend itself to our belief independently of any kind of evidence other than our instinct urging us to regard it favorably." For Peirce, plausibility does not depend on observed frequencies or probabilities, or on verisimilitude, or even on testability, which is not a question of the critique of the hypothetical inference as an inference, but rather a question of the hypothesis's relation to the inquiry process.The phrase "inference to the best explanation" (not used by Peirce but often applied to hypothetical inference) is not always understood as referring to the most simple and natural. However, in other senses of "best", such as "standing up best to tests", it is hard to know which is the best explanation to form, since one has not tested it yet.
Methodology of inquiry
At the methodeutical level Peirce held that a hypothesis is judged and selected for testing because it offers, via its trial, to expedite and economize the inquiry process itself toward new truths, first of all by being testable and also by further economies, in terms of cost, value, and relationships among guesses (hypotheses). Here, considerations such as probability, absent from the treatment of abduction at the critical level, come into play. For examples:- Cost: A simple but low-odds guess, if low in cost to test for falsity, may belong first in line for testing, to get it out of the way. If surprisingly it stands up to tests, that is worth knowing early in the inquiry, which otherwise might have stayed long on a wrong though seemingly likelier track.
- Value: A guess's objective probability recommends it for trial, while subjective likelihood can be misleading.
- Interrelationships: Guesses can be chosen for trial strategically, for which Peirce gave as example the game of Twenty QuestionsTwenty QuestionsTwenty Questions is a spoken parlor game which encourages deductive reasoning and creativity. It originated in the United States and escalated in popularity during the late 1940s when it became the format for a successful weekly radio quiz program....
.
In 1901 Peirce wrote, "There would be no logic in imposing rules, and saying that they ought to be followed, until it is made out that the purpose of hypothesis requires them." In 1903 Peirce called pragmatism
Pragmatism
Pragmatism is a philosophical tradition centered on the linking of practice and theory. It describes a process where theory is extracted from practice, and applied back to practice to form what is called intelligent practice...
"the logic of abduction" and said that the pragmatic maxim
Pragmatic maxim
The pragmatic maxim, also known as the maxim of pragmatism or the maxim of pragmaticism, is a maxim of logic formulated by Charles Sanders Peirce...
gives the necessary and sufficient logical rule to abduction in general. The pragmatic maxim is: "Consider what effects, that might conceivably have practical bearings, we conceive the object of our conception to have. Then, our conception of these effects is the whole of our conception of the object." It is a method for fruitful clarification of conceptions by equating the meaning of a conception with the conceivable practical implications of its object's conceived effects. Peirce held that that is precisely tailored to abduction's purpose in inquiry, the forming of an idea that could conceivably shape informed conduct. In various writings in the 1900s he said that the conduct of abduction (or retroduction) is governed by considerations of economy, belonging in particular to the economics of research. He regarded economics as a normative science whose analytic portion might be part of logical methodeutic.
Other writers
Norwood Russell HansonNorwood Russell Hanson
Norwood Russell Hanson was a philosopher of science. Hanson was a pioneer in advancing the argument that observation is theory-laden – that observation language and theory language are deeply interwoven – and that historical and contemporary comprehension are similarly deeply interwoven...
, a philosopher of science, wanted to grasp a logic explaining how scientific discoveries take place. He used Peirce's notion of abduction for this.
Further development of the concept can be found in Peter Lipton
Peter Lipton
Peter Lipton was the Hans Rausing Professor and Head of the Department of History and Philosophy of Science at Cambridge University, and a fellow of King's College, until his unexpected death in November 2007...
's Inference to the Best Explanation (Lipton, 1991).
Applications
Applications in artificial intelligenceArtificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
include fault diagnosis
Diagnosis (artificial intelligence)
As a subfield in artificial intelligence, Diagnosis is concerned with the development of algorithms and techniques that are able to determine whether the behaviour of a system is correct. If the system is not functioning correctly, the algorithm should be able to determine, as accurately as...
, belief revision
Belief revision
Belief revision is the process of changing beliefs to take into account a new piece of information. The logical formalization of belief revision is researched in philosophy, in databases, and in artificial intelligence for the design of rational agents....
, and automated planning. The most direct application of abduction is that of automatically detecting faults in systems: given a theory relating faults with their effects and a set of observed effects, abduction can be used to derive sets of faults that are likely to be the cause of the problem.
Abduction can also be used to model automated planning. Given a logical theory relating action occurrences with their effects (for example, a formula of the event calculus
Event calculus
The event calculus is a logical language for representing and reasoning about actions and their effects first presented by Robert Kowalski and Marek Sergot in 1986.It was extended by Murray Shanahan and Rob Miller in the 1990s....
), the problem of finding a plan for reaching a state can be modeled as the problem of abducting a set of literals implying that the final state is the goal state.
In intelligence analysis
Intelligence analysis
Intelligence analysis is the process of taking known information about situations and entities of strategic, operational, or tactical importance, characterizing the known, and, with appropriate statements of probability, the future actions in those situations and by those entities...
, Analysis of Competing Hypotheses
Analysis of Competing Hypotheses
The Analysis of Competing Hypotheses provides an unbiased methodology for evaluating multiple competing hypotheses for observed data. It was developed by Richards J. Heuer, Jr., a 45-year veteran of the Central Intelligence Agency, in the 1970s for use by the Agency and is used by analysts in...
and Bayesian network
Bayesian network
A Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
s, probabilistic abductive reasoning is used extensively. Similarly in medical diagnosis
Medical diagnosis
Medical diagnosis refers both to the process of attempting to determine or identify a possible disease or disorder , and to the opinion reached by this process...
and legal reasoning, the same methods are being used, although there have been many examples of errors, especially caused by the base rate fallacy
Base rate fallacy
The base rate fallacy, also called base rate neglect or base rate bias, is an error that occurs when the conditional probability of some hypothesis H given some evidence E is assessed without taking into account the "base rate" or "prior probability" of H and the total probability of evidence...
and the prosecutor's fallacy
Prosecutor's fallacy
The prosecutor's fallacy is a fallacy of statistical reasoning made in law where the context in which the accused has been brought to court is falsely assumed to be irrelevant to judging how confident a jury can be in evidence against them with a statistical measure of doubt...
.
Belief revision
Belief revision
Belief revision is the process of changing beliefs to take into account a new piece of information. The logical formalization of belief revision is researched in philosophy, in databases, and in artificial intelligence for the design of rational agents....
, the process of adapting beliefs in view of new information, is another field in which abduction has been applied. The main problem of belief revision is that the new information may be inconsistent with the corpus of beliefs, while the result of the incorporation cannot be inconsistent. This process can be done by the use of abduction: once an explanation for the observation has been found, integrating it does not generate inconsistency. This use of abduction is not straightforward, as adding propositional formula
Propositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
e to other propositional formulae can only make inconsistencies worse. Instead, abduction is done at the level of the ordering of preference of the possible worlds. Preference models use fuzzy logic or utility models.
In the philosophy of science
Philosophy of science
The philosophy of science is concerned with the assumptions, foundations, methods and implications of science. It is also concerned with the use and merit of science and sometimes overlaps metaphysics and epistemology by exploring whether scientific results are actually a study of truth...
, abduction has been the key inference method to support scientific realism
Scientific realism
Scientific realism is, at the most general level, the view that the world described by science is the real world, as it is, independent of what we might take it to be...
, and much of the debate about scientific realism is focused on whether abduction is an acceptable method of inference.
In historical linguistics
Historical linguistics
Historical linguistics is the study of language change. It has five main concerns:* to describe and account for observed changes in particular languages...
, abduction during language acquisition is often taken to be an essential part of processes of language change
Language change
Language change is the phenomenon whereby phonetic, morphological, semantic, syntactic, and other features of language vary over time. The effect on language over time is known as diachronic change. Two linguistic disciplines in particular concern themselves with studying language change:...
such as reanalysis and analogy
Analogy
Analogy is a cognitive process of transferring information or meaning from a particular subject to another particular subject , and a linguistic expression corresponding to such a process...
.
In anthropology
Anthropology
Anthropology is the study of humanity. It has origins in the humanities, the natural sciences, and the social sciences. The term "anthropology" is from the Greek anthrōpos , "man", understood to mean mankind or humanity, and -logia , "discourse" or "study", and was first used in 1501 by German...
, Alfred Gell
Alfred Gell
Alfred Gell was a British social anthropologist whose most influential work concerned art, language, symbolism and ritual. He was trained by Edmund Leach and Raymond Firth and did his fieldwork in Melanesia and tribal India...
in his influential book Art and Agency defined abduction, (after Eco) as “a case of synthetic inference 'where we find some very curious circumstances, which would be explained by the supposition that it was a case of some general rule, and thereupon adopt that supposition”. Gell criticizes existing 'anthropological' studies of art, for being too preoccupied with aesthetic value and not preoccupied enough with the central anthropological concern of uncovering 'social relationships' specifically the social contexts in which artworks are produced, circulated, and received. Abduction is used as the basis of one gets from art to agency in the sense of a theory of how works of art can inspire a sensus communis, or the commonly-held views that a characteristic of a given society because they are shared by everyone in that society. The question Gell asks in the book is, ‘how does initially to ‘speak’ to people?’ He answers by saying that “No reasonable person could suppose that art-like relations between people and things do not involve at least some form of semiosis
Semiosis
Semiosis is any form of activity, conduct, or process that involves signs, including the production of meaning. Briefly – semiosis is sign process...
.” However, he rejects any intimation that semiosis can be thought of as a language because then he would have to admit to some pre-established existence of the sensus communis that he wants to claim only emerges afterward out of art. Abduction is the answer to this conundrum because the tentative nature of the abduction concept (Pierce likened it to guessing) means that not only can it operate outside of any pre-existing framework, but moreover, it can actually intimate the existence of a framework. As Gell reasons in his analysis, the physical existence of the artwork prompts the viewer to perform an abduction that imbues the artwork with intentionality. A statue of a goddess, for example, in some senses actually becomes the goddess in the mind of the beholder; and represents not only the form of the deity but also her intentions (which are adduced from the feeling of her very presence). Therefore through abduction, Gell claims that art can have the kind of agency that plants the seeds that grow into cultural myths. The power of agency is the power to motivate actions and inspire ultimately the shared understanding that characterizes any given society.
External links
- "Abductive Inference in Reasoning and Perception", John R. Josephson, Laboratory for Artificial Intelligence Research, Ohio State University.
- "Deduction, Induction, and Abduction", Chapter 3 in article "Charles Sanders Peirce" by Robert Burch, 2001 and 2006, in the Stanford Encyclopedia of Philosophy.
- "Abduction", links to articles and websites on abductive inference, Martin Ryder.
- International Research Group on Abductive Inference, Uwe Wirth and Alexander Roesler, eds. Uses frames. Click on link at bottom of its home page for English. Wirth moved to U. of Gießen, Germany, and set up Abduktionsforschung, home page not in English but see Artikel section there. Abduktionsforschung home page via Google translation.
- "'You Know My Method': A Juxtaposition of Charles S. Peirce and Sherlock Holmes" (1981), by Thomas SebeokThomas SebeokThomas Albert Sebeok was a polymathic American semiotician and linguist.- Life and work :...
with Jean Umiker-Sebeok, from The Play of Musement, Thomas Sebeok, Bloomington, Indiana: Indiana University Press, pp. 17–52. - Commens Dictionary of Peirce's Terms, Mats Bergman and Sami Paavola, editors, Helsinki U. Peirce's own definitions, often many per term across the decades. There, see "Hypothesis [as a form of reasoning]", "Abduction", "Retroduction", and "Presumption [as a form of reasoning]".

