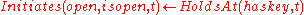Event calculus
Encyclopedia
The event calculus is a logic
al language for representing and reasoning about actions and their effects first presented by Robert Kowalski
and Marek Sergot in 1986.
It was extended by Murray Shanahan and Rob Miller in the 1990s.
The basic components of the event calculus, as with other similar languages for reasoning about actions and change are fluent
s and actions. In the event calculus, one can specify the value of fluents at some given time points, the actions that took place at given time points, and their effects.
s. A separate predicate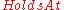 is used to tell which fluents hold at a given time point. For example,
is used to tell which fluents hold at a given time point. For example, 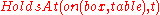 means that the box is on the table at time
means that the box is on the table at time  ; in this formula,
; in this formula, 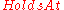 is a predicate while
is a predicate while  is a function.
is a function.
Actions are also represented as terms. The effects of actions are given using the predicates and
and  . In particular,
. In particular, 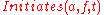 means that,
means that,
if the action represented by the term is executed at time
is executed at time  ,
,
then the fluent will be true after
will be true after  .
.
The predicate has a similar meaning, with the only difference
predicate has a similar meaning, with the only difference
being that will be false and not true after
will be false and not true after  .
.
in a way that is similar to the successor state axioms of the situation calculus
: a fluent is true at time if and only if it has been made true in the past and has not been made false in the meantime.
if and only if it has been made true in the past and has not been made false in the meantime.

This formula means that the fluent represented by the term is true at time
is true at time  if:
if:
A similar formula is used to formalize the opposite case in which a fluent is false at a given time. Other formulae are also needed for correctly formalizing fluents before they have been effects of an action. These formulae are similar to the above, but is replaced by
is replaced by 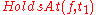 .
.
The predicate, stating that a fluent has been made false during an interval, can be axiomatized, or simply taken as a shorthand, as follows:
predicate, stating that a fluent has been made false during an interval, can be axiomatized, or simply taken as a shorthand, as follows:
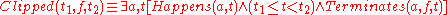
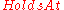 ,
,  and
and  , but do not specify which fluents are known to be true and which actions actually make fluents true or false. This is done by using a set of domain-dependent axioms. The known values of fluents are stated as simple literals
, but do not specify which fluents are known to be true and which actions actually make fluents true or false. This is done by using a set of domain-dependent axioms. The known values of fluents are stated as simple literals 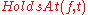 . The effects of actions are stated by formulae relating the effects of actions with their preconditions. For example, if the action
. The effects of actions are stated by formulae relating the effects of actions with their preconditions. For example, if the action  makes the fluent
makes the fluent  true, but only if
true, but only if  is currently true, the corresponding formula in the event calculus is:
is currently true, the corresponding formula in the event calculus is:
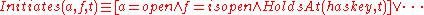
The right-hand expression of this equivalence is composed of a disjunction: for each action and fluent that can be made true by the action, there is a disjunct saying that is actually that action, that
is actually that action, that  is actually that fluent, and that the precondition of the action is met.
is actually that fluent, and that the precondition of the action is met.
The formula above specifies the truth value of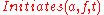 for every possible action and fluent. As a result, all effects of all actions have to be combined in a single formulae. This is a problem, because the addition of a new action requires modifying an existing formula rather than adding new ones. This problem can be solved by the application of circumscription to a set of formulae each specifying one effect of one action:
for every possible action and fluent. As a result, all effects of all actions have to be combined in a single formulae. This is a problem, because the addition of a new action requires modifying an existing formula rather than adding new ones. This problem can be solved by the application of circumscription to a set of formulae each specifying one effect of one action:
These formulae are simpler than the formula above, because each effect of each action can be specified separately. The single formula telling which actions and fluents
and fluents  make
make 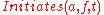 true has been replaced by a set of smaller formulae, each one telling the effect of an action to a fluent.
true has been replaced by a set of smaller formulae, each one telling the effect of an action to a fluent.
However, these formulae are not equivalent to the formula above. Indeed, they only specify sufficient conditions for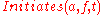 to be true, which should be completed by the fact that
to be true, which should be completed by the fact that  is false in all other cases. This fact can be formalized by simply circumscribing the predicate
is false in all other cases. This fact can be formalized by simply circumscribing the predicate  in the formula above. It is important to note that this circumscription is done only on the formulae specifying
in the formula above. It is important to note that this circumscription is done only on the formulae specifying  and not on the domain-independent axioms. The predicate
and not on the domain-independent axioms. The predicate  can be specified in the same way
can be specified in the same way  is.
is.
A similar approach can be taken for the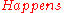 predicate. The evaluation of this predicate can be enforced by formulae specifying not only when it is true and when it is false:
predicate. The evaluation of this predicate can be enforced by formulae specifying not only when it is true and when it is false:
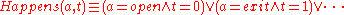
Circumscription can simplify this specification, as only necessary conditions can be specified:
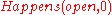
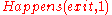
Circumscribing the predicate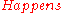 , this predicate will be false in all points in which it is not explicitly specified to be true. This circumscription has to be done separately from the circumscription of the other formulae. In other words, if
, this predicate will be false in all points in which it is not explicitly specified to be true. This circumscription has to be done separately from the circumscription of the other formulae. In other words, if  is the set of formulae of the kind
is the set of formulae of the kind 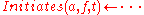 ,
,  is the set of formulae
is the set of formulae  , and
, and  are the domain independent axioms, the correct formulation of the domain is:
are the domain independent axioms, the correct formulation of the domain is:

program.
In fact, circumscription is one of the several semantics that can be given to negation as failure, and is closely related to the completion semantics (in which "if" is interpreted as "if and only if" — see logic programming
).
calculus can also formalize non-deterministic actions, concurrent actions, actions with delayed effects, gradual changes, actions with duration, continuous change, and non-inertial fluents.
Kave Eshghi showed how the event calculus can be used for planning, using abduction to generate hypothetical events in abductive logic programming
. Van Lambalgen and Hamm showed how the event calculus can also be used to give an algorithmic semantics to tense and aspect in natural language using constraint logic programming.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
al language for representing and reasoning about actions and their effects first presented by Robert Kowalski
Robert Kowalski
Robert "Bob" Anthony Kowalski is a British logician and computer scientist, who has spent most of his career in the United Kingdom....
and Marek Sergot in 1986.
It was extended by Murray Shanahan and Rob Miller in the 1990s.
The basic components of the event calculus, as with other similar languages for reasoning about actions and change are fluent
Fluent (artificial intelligence)
In artificial intelligence, a fluent is a condition that can change over time. In logical approaches to reasoning about actions, fluents can be represented in first-order logic by predicates having an argument that depends on time...
s and actions. In the event calculus, one can specify the value of fluents at some given time points, the actions that took place at given time points, and their effects.
Fluents and actions
In the event calculus, fluents are reified. This means that statements are not formalized as predicates but as functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s. A separate predicate
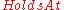 is used to tell which fluents hold at a given time point. For example,
is used to tell which fluents hold at a given time point. For example, 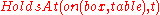 means that the box is on the table at time
means that the box is on the table at time  ; in this formula,
; in this formula, 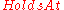 is a predicate while
is a predicate while  is a function.
is a function.Actions are also represented as terms. The effects of actions are given using the predicates
 and
and  . In particular,
. In particular, 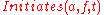 means that,
means that,if the action represented by the term
 is executed at time
is executed at time  ,
,then the fluent
 will be true after
will be true after  .
.The
 predicate has a similar meaning, with the only difference
predicate has a similar meaning, with the only differencebeing that
 will be false and not true after
will be false and not true after  .
.Domain-independent axioms
Like other languages for representing actions, the event calculus formalizes the correct evolution of the fluent via formulae telling the value of each fluent after an arbitrary action has been performed. The event calculus solves the frame problemFrame problem
In artificial intelligence, the frame problem was initially formulated as the problem of expressing a dynamical domain in logic without explicitly specifying which conditions are not affected by an action. John McCarthy and Patrick J. Hayes defined this problem in their 1969 article, Some...
in a way that is similar to the successor state axioms of the situation calculus
Situation calculus
The situation calculus is a logic formalism designed for representing and reasoning about dynamical domains. It was first introduced by John McCarthy in 1963. The main version of the situational calculus that is presented in this article is based on that introduced by Ray Reiter in 1991...
: a fluent is true at time
 if and only if it has been made true in the past and has not been made false in the meantime.
if and only if it has been made true in the past and has not been made false in the meantime.
This formula means that the fluent represented by the term
 is true at time
is true at time  if:
if:- an action
 has taken place:
has taken place: 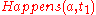 ;
; - this took place in the past:
 ;
; - this action has the fluent as an effect:
 ;
; - the fluent has not been made false in the meantime:

A similar formula is used to formalize the opposite case in which a fluent is false at a given time. Other formulae are also needed for correctly formalizing fluents before they have been effects of an action. These formulae are similar to the above, but
 is replaced by
is replaced by 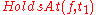 .
.The
 predicate, stating that a fluent has been made false during an interval, can be axiomatized, or simply taken as a shorthand, as follows:
predicate, stating that a fluent has been made false during an interval, can be axiomatized, or simply taken as a shorthand, as follows: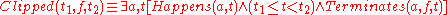
Domain-dependent axioms
The axioms above relate the value of the predicates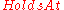 ,
,  and
and  , but do not specify which fluents are known to be true and which actions actually make fluents true or false. This is done by using a set of domain-dependent axioms. The known values of fluents are stated as simple literals
, but do not specify which fluents are known to be true and which actions actually make fluents true or false. This is done by using a set of domain-dependent axioms. The known values of fluents are stated as simple literals 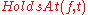 . The effects of actions are stated by formulae relating the effects of actions with their preconditions. For example, if the action
. The effects of actions are stated by formulae relating the effects of actions with their preconditions. For example, if the action 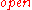 makes the fluent
makes the fluent  true, but only if
true, but only if 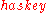 is currently true, the corresponding formula in the event calculus is:
is currently true, the corresponding formula in the event calculus is: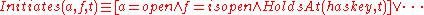
The right-hand expression of this equivalence is composed of a disjunction: for each action and fluent that can be made true by the action, there is a disjunct saying that
 is actually that action, that
is actually that action, that  is actually that fluent, and that the precondition of the action is met.
is actually that fluent, and that the precondition of the action is met.The formula above specifies the truth value of
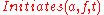 for every possible action and fluent. As a result, all effects of all actions have to be combined in a single formulae. This is a problem, because the addition of a new action requires modifying an existing formula rather than adding new ones. This problem can be solved by the application of circumscription to a set of formulae each specifying one effect of one action:
for every possible action and fluent. As a result, all effects of all actions have to be combined in a single formulae. This is a problem, because the addition of a new action requires modifying an existing formula rather than adding new ones. This problem can be solved by the application of circumscription to a set of formulae each specifying one effect of one action:These formulae are simpler than the formula above, because each effect of each action can be specified separately. The single formula telling which actions
 and fluents
and fluents  make
make 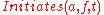 true has been replaced by a set of smaller formulae, each one telling the effect of an action to a fluent.
true has been replaced by a set of smaller formulae, each one telling the effect of an action to a fluent.However, these formulae are not equivalent to the formula above. Indeed, they only specify sufficient conditions for
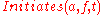 to be true, which should be completed by the fact that
to be true, which should be completed by the fact that  is false in all other cases. This fact can be formalized by simply circumscribing the predicate
is false in all other cases. This fact can be formalized by simply circumscribing the predicate  in the formula above. It is important to note that this circumscription is done only on the formulae specifying
in the formula above. It is important to note that this circumscription is done only on the formulae specifying  and not on the domain-independent axioms. The predicate
and not on the domain-independent axioms. The predicate  can be specified in the same way
can be specified in the same way  is.
is.A similar approach can be taken for the
 predicate. The evaluation of this predicate can be enforced by formulae specifying not only when it is true and when it is false:
predicate. The evaluation of this predicate can be enforced by formulae specifying not only when it is true and when it is false: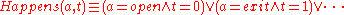
Circumscription can simplify this specification, as only necessary conditions can be specified:
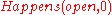
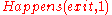
Circumscribing the predicate
 , this predicate will be false in all points in which it is not explicitly specified to be true. This circumscription has to be done separately from the circumscription of the other formulae. In other words, if
, this predicate will be false in all points in which it is not explicitly specified to be true. This circumscription has to be done separately from the circumscription of the other formulae. In other words, if  is the set of formulae of the kind
is the set of formulae of the kind 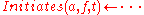 ,
,  is the set of formulae
is the set of formulae  , and
, and  are the domain independent axioms, the correct formulation of the domain is:
are the domain independent axioms, the correct formulation of the domain is:
The event calculus as a logic program
The event calculus was originally formulated as a set of Horn clauses augmented with negation as failure and could be run as a PrologProlog
Prolog is a general purpose logic programming language associated with artificial intelligence and computational linguistics.Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is declarative: the program logic is expressed in terms of...
program.
In fact, circumscription is one of the several semantics that can be given to negation as failure, and is closely related to the completion semantics (in which "if" is interpreted as "if and only if" — see logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
).
Extensions and applications
The original event calculus paper of Kowalski and Sergot focused on applications to database updates and narratives. Extensions of the eventcalculus can also formalize non-deterministic actions, concurrent actions, actions with delayed effects, gradual changes, actions with duration, continuous change, and non-inertial fluents.
Kave Eshghi showed how the event calculus can be used for planning, using abduction to generate hypothetical events in abductive logic programming
Abductive logic programming
Abductive logic programming is a high level knowledge-representation framework that can be used to solve problems declaratively based on abductive reasoning. It extends normal logic programming by allowing some predicates to be incompletely defined, declared as abducible predicates...
. Van Lambalgen and Hamm showed how the event calculus can also be used to give an algorithmic semantics to tense and aspect in natural language using constraint logic programming.