Abel's irreducibility theorem
Encyclopedia
In mathematics, Abel's irreducibility theorem, a field theory
result described in 1829 by Niels Henrik Abel
, asserts that if ƒ(x) is a polynomial over the a field
F that shares a root with an irreducible polynomial
g(x), then ƒ(x) is divisible evenly by g(x) (i.e. ƒ(x) can be factored as g(x)h(x) with h having coefficients in F). In other words, if a polynomial shares at least one root with an irreducible polynomial, it necessarily shares all the roots of the irreducible polynomial.
Corollaries of the theorem include:
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
result described in 1829 by Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
, asserts that if ƒ(x) is a polynomial over the a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F that shares a root with an irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
g(x), then ƒ(x) is divisible evenly by g(x) (i.e. ƒ(x) can be factored as g(x)h(x) with h having coefficients in F). In other words, if a polynomial shares at least one root with an irreducible polynomial, it necessarily shares all the roots of the irreducible polynomial.
Corollaries of the theorem include:
- If ƒ(x) is irreducible, there is no lower-degree polynomial (other than the zero polynomial) that shares any root with it. For example, x2 − 2 is irreducible over the rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s and has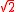
as a root; hence there is no linear or constant polynomial over the rationals having 
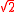as a root. Furthermore, there is no same-degree polynomial that shares any roots with ƒ(x), other than constant multiples of ƒ(x). - If ƒ(x) ≠ g(x) are both monic irreducible, they share no roots.