Above threshold ionization
Encyclopedia
Above Threshold Ionization – in quantum mechanics
ionization
of the atom with the electromagnetic radiation
with violation of Einstein formula
i.e. when the kinetic energy of emitted electrons is larger than the difference between the photon energy and the ionization energy or the work function
. In that case the generalized Einstein formula is valid
where
is the arbitrary integer number, 
is the ionization energy
(work function
) and
is the electron kinetic energy. This phenomenon is measurable only if the electromagnetic field is comparable with the field which keeps the electrons in the atom
, for example generated with a very strong laser
. With this method one can generate for example the beta radiation. In practice the spectrum
of electron energies is continuous with the very strong sharp maxima around the condition of the generalized Einstein formula for lower fields which are barely visible in the plateau for very strong fields and also depends on the characteristics of the detector.
required to be ionized. The ATI spectrum consists of a series of peaks equally separated by the photon energy.
Above Threshold Ionization may be explained by solving the time-dependent Schrödinger equation in the approximate manner. The Schrödinger equation for the free electron in the field of the electromagnetic wave in one dimension and in the radiation gauge is given by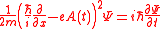
,
where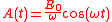
so the electric field is given by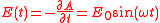
Substituting
we are obtaining the equation for
with the solution
,
where
.
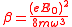
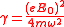The Schrödinger equation for the electron in the wave field and in the atomic potential will be given by
,
where,
is the Hamiltonian of the free electron in the field. Adding and subtracting the energy of the ground state from which the electron is to be ionized we obtain
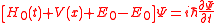
Because in the ground state the electron kinetic energy is equall the total energy but with the opposite sign (virial theorem) and only this energy will be left after the fast removal of the electron, we neglect in this equation the sum
for all 
and obtain the approximate equation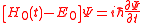
,
where the only remaining of the atomic potential is the constant.
This equation may now be solved using the previous result for the free electron in the field and expanding the ground state into its Fourier components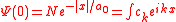
,
with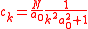
This equation has therefore the solution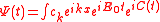
We obtain the ionization spectrum from the formula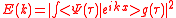
,
telling how much of the plane wave of the free electron with the given kinetic energy is at the and of the ionization process, where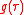
is the averaging function of the measuring detector for example
.
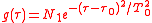Expanding the factor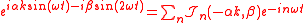
with the generalized Bessel function
s
defined by the inverse transform, we obtain
(
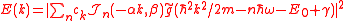
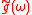
is the Fourier transform of the detector function) therefore the sum of sharp or fuzzy maxima localized around the energy condition of emitted electrons
depending on the speed i.e. the averaging parameter of the detector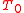 
.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
ionization
Ionization
Ionization is the process of converting an atom or molecule into an ion by adding or removing charged particles such as electrons or other ions. This is often confused with dissociation. A substance may dissociate without necessarily producing ions. As an example, the molecules of table sugar...
of the atom with the electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
with violation of Einstein formula
Photoelectric effect
In the photoelectric effect, electrons are emitted from matter as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons...
i.e. when the kinetic energy of emitted electrons is larger than the difference between the photon energy and the ionization energy or the work function
Photoelectric effect
In the photoelectric effect, electrons are emitted from matter as a consequence of their absorption of energy from electromagnetic radiation of very short wavelength, such as visible or ultraviolet light. Electrons emitted in this manner may be referred to as photoelectrons...
. In that case the generalized Einstein formula is valid
where
is the arbitrary integer number, is the ionization energyIonization energy
The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove an electron from the species to a practically infinite distance. Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.The property...
(work function
Work function
In solid-state physics, the work function is the minimum energy needed to remove an electron from a solid to a point immediately outside the solid surface...
) and
is the electron kinetic energy. This phenomenon is measurable only if the electromagnetic field is comparable with the field which keeps the electrons in the atomAtom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
, for example generated with a very strong laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
. With this method one can generate for example the beta radiation. In practice the spectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
of electron energies is continuous with the very strong sharp maxima around the condition of the generalized Einstein formula for lower fields which are barely visible in the plateau for very strong fields and also depends on the characteristics of the detector.
Theory
Above-threshold ionization (ATI), a well studied process by now, is a process in which atoms absorb more than the minimum number of photonsrequired to be ionized. The ATI spectrum consists of a series of peaks equally separated by the photon energy.
Above Threshold Ionization may be explained by solving the time-dependent Schrödinger equation in the approximate manner. The Schrödinger equation for the free electron in the field of the electromagnetic wave in one dimension and in the radiation gauge is given by
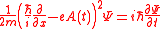,where
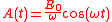
so the electric field is given by
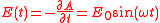
Substituting
we are obtaining the equation for
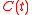
with the solution
,where
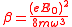
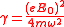.The Schrödinger equation for the electron in the wave field and in the atomic potential will be given by
,where,
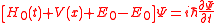
is the Hamiltonian of the free electron in the field. Adding and subtracting the energy of the ground state from which the electron is to be ionized we obtainBecause in the ground state the electron kinetic energy is equall the total energy but with the opposite sign (virial theorem) and only this energy will be left after the fast removal of the electron, we neglect in this equation the sum
for all and obtain the approximate equation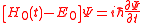,where the only remaining of the atomic potential is the constant.
This equation may now be solved using the previous result for the free electron in the field and expanding the ground state into its Fourier components
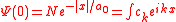,with
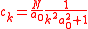
This equation has therefore the solution
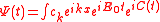
We obtain the ionization spectrum from the formula
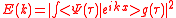,telling how much of the plane wave of the free electron with the given kinetic energy is at the and of the ionization process, where
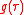is the averaging function of the measuring detector for example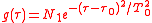.Expanding the factor
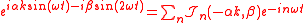
with the generalized Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s
defined by the inverse transform, we obtain(
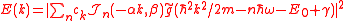
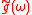
is the Fourier transform of the detector function) therefore the sum of sharp or fuzzy maxima localized around the energy condition of emitted electrons
depending on the speed i.e. the averaging parameter of the detector .