In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the absolute Galois group G_K of a field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

 K is the Galois group

Galois group

In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...

 of K^sep over K, where K^sep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure

Algebraic closure

In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....

 of K that fix K. The absolute Galois group is unique up to

Up to

In mathematics, the phrase "up to x" means "disregarding a possible difference in  x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...

 isomorphism. It is a profinite group.

(When K is a perfect field

Perfect field

In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...

, K^sep is the same as an algebraic closure

Algebraic closure

In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....

 K^alg of K. This holds e.g. for K of characteristic zero, or K a finite field

Finite field

In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...

.)

Examples

• The absolute Galois group of an algebraically closed field is trivial.
• The absolute Galois group of the real number
  Real number
  In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
  
  s is a cyclic group of two elements (complex conjugation and the identity map), since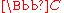 is the separable closure of and .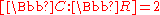
• The absolute Galois group of a finite field
  Finite field
  In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
  
   K is isomorphic to the group

.

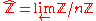The Frobenius automorphism Fr is a canonical (topological) generator of G_K. (Recall that Fr(x) = x^q for all x in K^alg, where q is the number of elements in K.)

• The absolute Galois group of the field of rational functions with complex coefficients is free (as a profinite group). This result is due to Adrien Douady
  Adrien Douady
  Adrien Douady was a French mathematician.He was a student of Henri Cartan at the Ecole Normale Supérieure, and initially worked in homological algebra. His thesis concerned deformations of complex analytic spaces...
  
   and has its origins in Riemann's existence theorem.
• More generally, Let C be an algebraically closed field and x a variable. Then the absolute Galois group of K=C(x) is free of rank equal to the cardinality of C. This result is due to David Harbater
  David Harbater
  David Harbater is an American mathematician, well known for his work in Galois theory, algebraic geometry and arithmetic geometry.-Life and work:...
  
   and Florian Pop
  Florian Pop
  Florian Pop is a Romanian mathematician, a professor of mathematics at the University of Pennsylvania.Pop received his Ph.D. in 1987 and his habilitation in 1991, both from the University of Heidelberg...
  
  , and was also proved later by Dan Haran and Moshe Jarden using algebraic methods.
• Let K be a finite extension of the p-adic number
  P-adic number
  In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
  
  s Q_p. For p ≠ 2, its absolute Galois group is generated by [K:Q_p] + 3 elements and has an explicit description by generators and relations. This is a result of Uwe Jannsen and Kay Wingberg. Some results are known in the case p = 2, but the structure for Q₂ is not known.
• Another case in which the absolute Galois group has been determined is for the largest totally real subfield of the field of algebraic numbers.

Problems

• No direct description is known for the absolute Galois group of the rational number
  Rational number
  In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
  
  s. In this case, it follows from Belyi's theorem
  Belyi's theorem
  In mathematics, Belyi's theorem on algebraic curves states that any non-singular algebraic curve C, defined by algebraic number coefficients, represents a compact Riemann surface which is a ramified covering of the Riemann sphere, ramified at three points only.It follows that the Riemann surface in...
  
   that the absolute Galois group has a faithful action on the dessins d'enfants of Grothendieck (maps on surfaces), enabling us to "see" the Galois theory of algebraic number fields.

• Let K be the maximal abelian extension
  Abelian extension
  In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
  
   of the rational numbers. Then Shafarevich's conjecture asserts that the absolute Galois group of G_K is a free profinite group.

Some general results

• Every profinite group occurs as a Galois group of some Galois extension, however not every profinite group occurs as an absolute Galois group. For example, the Artin-Schreier Theorem
  Real closed field
  In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
  
   asserts that the only finite absolute Galois groups are the trivial one and the cyclic group of order 2.

• Every projective profinite group can be realized as an absolute Galois group of a Pseudo algebraically closed field
  Pseudo algebraically closed field
  In mathematics, a field K is pseudo algebraically closed if it satisfies certain properties which hold for any algebraically closed field.-Formulation:...
  
  . This result is due to Alexander Lubotzky
  Alexander Lubotzky
  Professor Alexander Lubotzky is an Israeli academic and former politician. A former head of the Mathematics Institute at the Hebrew University of Jerusalem, he served as a member of the Knesset for The Third Way party between 1996 and 1999.-Education:...
  
   and Lou van den Dries.