
Pseudo algebraically closed field
Encyclopedia
In mathematics
, a field
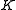 is pseudo algebraically closed if it satisfies certain properties which hold for any algebraically closed field
is pseudo algebraically closed if it satisfies certain properties which hold for any algebraically closed field
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
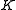 is pseudo algebraically closed if it satisfies certain properties which hold for any algebraically closed field
is pseudo algebraically closed if it satisfies certain properties which hold for any algebraically closed fieldAlgebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
.
Formulation
A field K is pseudo algebraically closed field (usually abbreviated by PAC) if one of the following equivalent conditions holds:- Each absolutely irreducibleAbsolutely irreducibleIn mathematics, absolutely irreducible is a term applied to linear representations or algebraic varieties over a field. It means that the object in question remains irreducible, even after any finite extension of the field of coefficients...
variety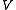 defined over
defined over  has a
has a  -rational point.
-rational point. - For each absolutely irreducible polynomial
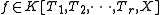 with
with  and for each nonzero
and for each nonzero  there exists
there exists  such that
such that 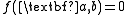 and
and  .
. - Each absolutely irreducible polynomial
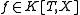 has infinitely many
has infinitely many 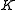 -rational points.
-rational points. - If
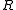 is a finitely generated integral domain over
is a finitely generated integral domain over  with quotient field which is regular over
with quotient field which is regular over 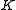 , then there exist a homomorphism
, then there exist a homomorphism 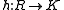 such that
such that 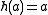 for each
for each 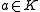
Examples
- Algebraically closed fields and separably closed fields are always PAC.
- A non-principal ultraproductUltraproductThe ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
of distinct finite fields is PAC (consequence of Riemann Hypothesis for function fields).
- Infinite algebraic extensionAlgebraic extensionIn abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
s of finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s are PAC (consequence of Riemann Hypothesis for function fields).
- This example arises from measure theory: The absolute Galois groupAbsolute Galois groupIn mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
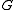 of a field
of a field  is profinite, hence compactCompact groupIn mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
is profinite, hence compactCompact groupIn mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
, and hence equipped with a normalized Haar measureHaar measureIn mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
. Let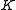 be a countable Hilbertian field and let
be a countable Hilbertian field and let  be a positive integer. Then for almost all
be a positive integer. Then for almost all  -tuple
-tuple  , the fixed field of the subgroup generated by the automorphisms is PAC. Here the phrase "almost all" means "all but a set of measure zero". (This result is a consequence of Hilbert's irreducibility theorem.)
, the fixed field of the subgroup generated by the automorphisms is PAC. Here the phrase "almost all" means "all but a set of measure zero". (This result is a consequence of Hilbert's irreducibility theorem.)
- Let K be the maximal totally real Galois extension of the rational numbers and i the square root of -1. Then K(i) is PAC.

