
Abstract elementary class
Encyclopedia
In model theory
, an abstract elementary class, or AEC for short, is a class of models with a partial order similar to the relation of a substructure
of an elementary class
in first-order
model theory. They were studied by .
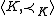 , for K a class of structures in some language L, is an AEC if it has the following properties:
, for K a class of structures in some language L, is an AEC if it has the following properties:
analogous to Morley's categoricity theorem
in first-order model theory.
The conjecture states, in simple terms, for every AEC K there is some cardinal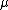 (which depends only on
(which depends only on 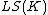 ) such that if K is categorical at some
) such that if K is categorical at some 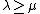 , ie. every model of size
, ie. every model of size 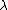 is isomorphic, then K is categorical at all
is isomorphic, then K is categorical at all 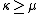 .
.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, an abstract elementary class, or AEC for short, is a class of models with a partial order similar to the relation of a substructure
Substructure
In mathematical logic, an substructure or subalgebra is a structure whose domain is a subset of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure...
of an elementary class
Elementary class
In the branch of mathematical logic called model theory, an elementary class is a class consisting of all structures satisfying a fixed first-order theory.- Definition :...
in first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
model theory. They were studied by .
Definition
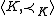 , for K a class of structures in some language L, is an AEC if it has the following properties:
, for K a class of structures in some language L, is an AEC if it has the following properties:
-
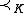 is a partial order on K
is a partial order on K - If
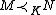 then
then 
- Isomorphisms: K is closed under isomorphismsIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, and if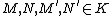 such that
such that 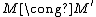 ,
, 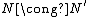 , and
, and 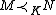 then
then 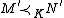
- Coherence: If
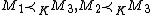 , and
, and 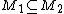 then
then 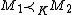
- Tarski-Vaught ChainTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
Axioms If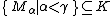 is a chain, ie.
is a chain, ie. 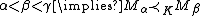
-
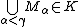
- if
 , for all
, for all 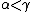 , then
, then 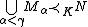
-
- Löwenheim–SkolemLöwenheim–Skolem theoremIn mathematical logic, the Löwenheim–Skolem theorem, named for Leopold Löwenheim and Thoralf Skolem, states that if a countable first-order theory has an infinite model, then for every infinite cardinal number κ it has a model of size κ...
Axiom There exists a cardinalCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
denoted by , such that if A is a subset of the universe of M, then there is M' in K whose universe contains A such that
, such that if A is a subset of the universe of M, then there is M' in K whose universe contains A such that 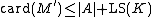 and
and 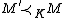
Examples
- Elementary classesElementary classIn the branch of mathematical logic called model theory, an elementary class is a class consisting of all structures satisfying a fixed first-order theory.- Definition :...
are the most basic example of an AEC, when taken with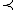 taken to be elementary substructureElementary substructureIn model theory, a field within mathematical logic, two structures M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order σ-sentences....
taken to be elementary substructureElementary substructureIn model theory, a field within mathematical logic, two structures M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order σ-sentences....
. - If
 is a cardinal,
is a cardinal, 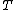 is a theory in the infinitary logicInfinitary logicAn infinitary logic is a logic that allows infinitely long statements and/or infinitely long proofs. Some infinitary logics may have different properties from those of standard first-order logic. In particular, infinitary logics may fail to be compact or complete. Notions of compactness and...
is a theory in the infinitary logicInfinitary logicAn infinitary logic is a logic that allows infinitely long statements and/or infinitely long proofs. Some infinitary logics may have different properties from those of standard first-order logic. In particular, infinitary logics may fail to be compact or complete. Notions of compactness and...
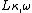 , and
, and 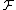 is a fragment of the
is a fragment of the 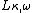 containing
containing 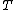 , then
, then 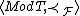 is an AEC.
is an AEC.
Shelah's Categoricity Conjecture
The work done on AECs is in large part done to prove Shelah's categoricity conjecture, which is a conjectureConjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
analogous to Morley's categoricity theorem
Morley's categoricity theorem
In model theory, a branch of mathematical logic, a theory is κ-categorical if it has exactly one model of cardinality κ up to isomorphism....
in first-order model theory.
The conjecture states, in simple terms, for every AEC K there is some cardinal
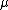 (which depends only on
(which depends only on 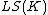 ) such that if K is categorical at some
) such that if K is categorical at some 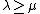 , ie. every model of size
, ie. every model of size 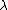 is isomorphic, then K is categorical at all
is isomorphic, then K is categorical at all 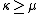 .
.Results
The following are some some important results about AECs:- Shelah's Presentation Theorem: Any AEC
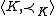 can be written as a PCPseudoelementary classIn logic, a pseudoelementary class is a class of structures derived from an elementary class by omitting some of its sorts and relations. It is the mathematical logic counterpart of the notion in category theory of a forgetful functor, and in physics of hidden variable theories purporting to...
can be written as a PCPseudoelementary classIn logic, a pseudoelementary class is a class of structures derived from an elementary class by omitting some of its sorts and relations. It is the mathematical logic counterpart of the notion in category theory of a forgetful functor, and in physics of hidden variable theories purporting to...
class, where the language is of size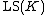 and we omit at most
and we omit at most 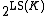 many types.
many types.

