Abu Kamil
Encyclopedia
(c. 850 – c. 930) was an Egyptian
Muslim
mathematician during the Islamic Golden Age
. He made important contributions to algebra
and geometry
, and considered the first mathematician to systematically use and accept irrational number
s as solutions and coefficients to equations. His mathematical techniques were later adopted by Fibonacci
, thus allowing Abu Kamil an important part in introducing algebra to Europe.
He was also the first Islamic mathematician to work easily with algebraic equations with powers higher than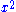
(up to 
), and solved sets of non-linear simultaneous equations
with three unknown variables
. He wrote all problems rhetorically, and some of his books lacked any mathematical notation
beside those of integers. For example, he uses the Arabic expression "māl māl shayʾ" ("square-square-thing") for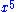
(i.e., 
).
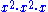was geared towards the general public, Abu Kamil was addressing other mathematicians, or readers familiar with Euclid
's Elements. Abu Kamil solves systems of equation
s whose solutions are whole numbers and fractions, and accepted irrational numbers (in the form of a square root
or fourth root
) as solutions and coefficient
s to quadratic equation
s.
The first chapter teaches algebra by solving problems of application to geometry, often involving an unknown variable and square roots. The second chapter deals with the six types of problems found in Al-Khawarizmi's book, but some of which, especially those of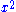
, were now worked out directly instead of first solving for 
and accompanied with geometrical illustrations and proofs. The third chapter contains examples of quadratic irrationalities as solutions and coefficients. The fourth chapter shows how these irrationalities are used to solve problems involving polygons. The rest of the book contains solutions for sets of indeterminate equations, problems of application in realistic situations, and problems involving unrealistic situations intended for recreational mathematics
.
A number of Islamic mathematicians wrote commentaries on this work, including al-Iṣṭakhrī al-Ḥāsib and ʿAli ibn Aḥmad al-ʿImrānī (d. 955-6), but both commentaries are now lost.
In Europe, similar material to this book is found in the writings of Fibonacci
, and some sections were incorporated and improved upon in the Latin work of John of Seville
, Liber mahameleth. A partial translation to Latin was done in the 14th-century by William of Luna, and in the 15th-century the whole work also appeared in a Hebrew translation by Mordekhai Finzi.
for indeterminate equations. It is the earliest known Arabic work where solutions are sought to the type of indeterminate equations found in Diophantus
's Arithmetica
. However, Abu Kamil explains certain methods not found in any extant copy of the Arithmetica. He also describes one problem for which he found 2,678 solutions.
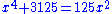to calculate a numerical approximation for the side of a regular pentagon
in a circle of radius 10. He also uses the Golden Ratio
in some of his calculations. Fibonacci
knew about this treatise and made extensive use of it in his Practica geometriae.
. The title is derived from a type of problems known in the east which involve the purchase of different species of birds. Abu Kamil wrote in the introduction:
According to Jacques Sesiano, Abu Kamil remained seemingly unparalleled throughout the Middle Ages in trying to find all the possible solutions to some of his problems.
for non-mathematicians, like land surveyors and other government officials. It presents a set rules for calculating the volume and surface area of solids (mainly rectangular parallelepipeds, right circular prism
s, square pyramid
s, and circular cones
). Its first few chapters also contain rules for determining the area
, diagonal
, perimeter
, etc, of different types of triangles, rectangles and squares.
Another lost work of his is the Book on Augmentation and Diminution (Kitāb al-jamʿ wa al-tafrīq), which gained more attention after historian Franz Woepcke
linked it with another Latin work, Liber augmenti et diminutionis.
He also wrote the Book of Estate Sharing using Algebra (Kitāb al-waṣāyā bi al-jabr wa al-muqābala), which contains algebraic solutions for problems of Islamic inheritance
and discusses the opinions of known jurists.
Ibn al-Nadīm
in his Fihrist listed the following additional titles: Book of Fortune (Kitāb al-falāḥ), Book of the Key to Fortune (Kitāb miftāḥ al-falāḥ), Book of the Adequate (Kitāb al-kifāya), and Book of the Kernel (Kitāb al-ʿasīr).
and Fibonacci
, and as such had a lasting impact on the development of algebra. Many of his examples and algebraic techniques were later copied by Fibonacci in his Practica geometriae and other works. Unmistakable borrowings, but without Abu Kamil being explicitly mentioned and perhaps mediated by lost treatises, are also found in Fibonacci's Liber Abaci
.
, and defended him against Ibn Barza who attributed the authority and precedent in algebra to his grandfather, [[ʿAbd al-Hamīd ibn Turk]].
Abu Kamil wrote in the introduction of his Algebra:
Egyptians
Egyptians are nation an ethnic group made up of Mediterranean North Africans, the indigenous people of Egypt.Egyptian identity is closely tied to geography. The population of Egypt is concentrated in the lower Nile Valley, the small strip of cultivable land stretching from the First Cataract to...
Muslim
Muslim
A Muslim, also spelled Moslem, is an adherent of Islam, a monotheistic, Abrahamic religion based on the Quran, which Muslims consider the verbatim word of God as revealed to prophet Muhammad. "Muslim" is the Arabic term for "submitter" .Muslims believe that God is one and incomparable...
mathematician during the Islamic Golden Age
Islamic Golden Age
During the Islamic Golden Age philosophers, scientists and engineers of the Islamic world contributed enormously to technology and culture, both by preserving earlier traditions and by adding their own inventions and innovations...
. He made important contributions to algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, and considered the first mathematician to systematically use and accept irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s as solutions and coefficients to equations. His mathematical techniques were later adopted by Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
, thus allowing Abu Kamil an important part in introducing algebra to Europe.
He was also the first Islamic mathematician to work easily with algebraic equations with powers higher than
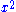(up to ), and solved sets of non-linear simultaneous equationsSimultaneous equations
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations...
with three unknown variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
. He wrote all problems rhetorically, and some of his books lacked any mathematical notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
beside those of integers. For example, he uses the Arabic expression "māl māl shayʾ" ("square-square-thing") for
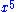(i.e., 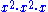).Book of Algebra
Known as Kitāb fi al-jabr wa al-muqābala, perhaps Abu Kamil's most influential work, which he intended to supersede and expand upon that of Al-Khawarizmi. Whereas the Algebra of al-KhawarizmiThe Compendious Book on Calculation by Completion and Balancing
, also known under a shorter name spelled as Hisab al-jabr w’al-muqabala, Kitab al-Jabr wa-l-Muqabala and other transliterations) is a mathematical book written in Arabic in approximately AD 820 by the Persian (Arabic for "The Compendious Book on Calculation by Completion and Balancing", in...
was geared towards the general public, Abu Kamil was addressing other mathematicians, or readers familiar with Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's Elements. Abu Kamil solves systems of equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s whose solutions are whole numbers and fractions, and accepted irrational numbers (in the form of a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
or fourth root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
) as solutions and coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s to quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
s.
The first chapter teaches algebra by solving problems of application to geometry, often involving an unknown variable and square roots. The second chapter deals with the six types of problems found in Al-Khawarizmi's book, but some of which, especially those of
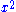, were now worked out directly instead of first solving for and accompanied with geometrical illustrations and proofs. The third chapter contains examples of quadratic irrationalities as solutions and coefficients. The fourth chapter shows how these irrationalities are used to solve problems involving polygons. The rest of the book contains solutions for sets of indeterminate equations, problems of application in realistic situations, and problems involving unrealistic situations intended for recreational mathematicsRecreational mathematics
Recreational mathematics is an umbrella term, referring to mathematical puzzles and mathematical games.Not all problems in this field require a knowledge of advanced mathematics, and thus, recreational mathematics often attracts the curiosity of non-mathematicians, and inspires their further study...
.
A number of Islamic mathematicians wrote commentaries on this work, including al-Iṣṭakhrī al-Ḥāsib and ʿAli ibn Aḥmad al-ʿImrānī (d. 955-6), but both commentaries are now lost.
In Europe, similar material to this book is found in the writings of Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
, and some sections were incorporated and improved upon in the Latin work of John of Seville
John of Seville
John of Seville was the main translator from Arabic into Castilian together with Dominicus Gundissalinus during the early days of the Toledo School of Translators....
, Liber mahameleth. A partial translation to Latin was done in the 14th-century by William of Luna, and in the 15th-century the whole work also appeared in a Hebrew translation by Mordekhai Finzi.
Book of Rare Things in the Art of Calculation
Kitāb al-ṭarā’if fi’l-ḥisāb, describes a number of systematic procedures for finding integral solutionsIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
for indeterminate equations. It is the earliest known Arabic work where solutions are sought to the type of indeterminate equations found in Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
's Arithmetica
Arithmetica
Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
. However, Abu Kamil explains certain methods not found in any extant copy of the Arithmetica. He also describes one problem for which he found 2,678 solutions.
On the Pentagon and Decagon
Kitāb … al-mukhammas wa’al-mu‘ashshar. In this treatise algebraic methods are used to solve geometrical problems. Abu Kamil uses the equation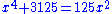 to calculate a numerical approximation for the side of a regular pentagonPentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
in a circle of radius 10. He also uses the Golden Ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
in some of his calculations. Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
knew about this treatise and made extensive use of it in his Practica geometriae.
Book of Birds
Kitāb al-ṭair, a small treatise teaching how to solve indeterminate linear systems with positive integral solutionsIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
. The title is derived from a type of problems known in the east which involve the purchase of different species of birds. Abu Kamil wrote in the introduction:
I found myself before a problem that I solved and for which I discovered a great many solutions; looking deeper for its solutions, I obtained two thousand six hundred and seventy-six correct ones. My astonishment about that was great, but I found out that, when I recounted this discovery, those who did not know me were arrogant, shocked, and suspicious of me. I thus decided to write a book on this kind of calculations, with the purpose of facilitating its treatment and making it more accessible.
According to Jacques Sesiano, Abu Kamil remained seemingly unparalleled throughout the Middle Ages in trying to find all the possible solutions to some of his problems.
On Measurement and Geometry
Kitāb al-misāḥa wa al-handasa, a manual of geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
for non-mathematicians, like land surveyors and other government officials. It presents a set rules for calculating the volume and surface area of solids (mainly rectangular parallelepipeds, right circular prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
s, square pyramid
Square pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :...
s, and circular cones
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
). Its first few chapters also contain rules for determining the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
, diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
, perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
, etc, of different types of triangles, rectangles and squares.
Lost works
Abu Kamil wrote a now lost treatise on the use of double false position, known as the Book of the Two Errors (Kitāb al-khaṭaʾayn).Another lost work of his is the Book on Augmentation and Diminution (Kitāb al-jamʿ wa al-tafrīq), which gained more attention after historian Franz Woepcke
Franz Woepcke
Franz Woepcke was a German Orientalist and mathematician. Woepcke is remembered for edition of numerous Arabic mathematical manuscripts....
linked it with another Latin work, Liber augmenti et diminutionis.
He also wrote the Book of Estate Sharing using Algebra (Kitāb al-waṣāyā bi al-jabr wa al-muqābala), which contains algebraic solutions for problems of Islamic inheritance
Islamic inheritance jurisprudence
Islamic Inheritance jurisprudence is a field of Islamic Jurisprudence that deals with inheritance, a topic that is prominently dealt with in the Qur'an. It is often called Mīrāth, and its branch of Islamic law is technically known as ʿulm al-farāʾiḍ...
and discusses the opinions of known jurists.
Ibn al-Nadīm
Ibn al-Nadim
Abu'l-Faraj Muhammad bin Is'hāq al-Nadim , whose father was known as al-Warrāq was a Shia Muslim scholar and bibliographer. Some scholars regard him as a Persian, but this is not certain. He is famous as the author of the Kitāb al-Fihrist...
in his Fihrist listed the following additional titles: Book of Fortune (Kitāb al-falāḥ), Book of the Key to Fortune (Kitāb miftāḥ al-falāḥ), Book of the Adequate (Kitāb al-kifāya), and Book of the Kernel (Kitāb al-ʿasīr).
Influence
The works of Abu Kamil influenced other mathematicians, like al-KarajiAl-Karaji
' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
and Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
, and as such had a lasting impact on the development of algebra. Many of his examples and algebraic techniques were later copied by Fibonacci in his Practica geometriae and other works. Unmistakable borrowings, but without Abu Kamil being explicitly mentioned and perhaps mediated by lost treatises, are also found in Fibonacci's Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
.
On al-Khawarizmi
Almost nothing is known about the life and career of Abu Kamil except that he was a successor of al-Khawarizmi, whom he never personally met. He was also one of the earliest mathematicians to recognize Al-Khwarizmi's contributions to algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, and defended him against Ibn Barza who attributed the authority and precedent in algebra to his grandfather, [[ʿAbd al-Hamīd ibn Turk]].
Abu Kamil wrote in the introduction of his Algebra:
I have studied with great attention the writings of the mathematicians, examined their assertions, and scrutinized what they explain in their works; I thus observed that the book by Muḥammad ibn Mūsā al-Khawārizmī known as Algebra is superior in the accuracy of its principle and the exactness of its argumentation. It thus behooves us, the community of mathematicians, to recognize his priority and to admit his knowledge and his superiority, as in writing his book on algebra he was an initiator and the discoverer of its principles, ...
Further reading
- Djebbar, Ahmed. Une histoire de la science arabe: Entretiens avec Jean Rosmorduc. Seuil (2001)