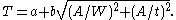Accot-Zhai steering law
Encyclopedia
The steering law in human–computer interaction
and ergonomics
is a predictive model of human movement that describes the time required to navigate, or steer, through a 2-dimensional tunnel. The tunnel can be thought of as a path or trajectory on a plane that has an associated thickness or width, where the width can vary along the tunnel. The goal of a steering task is to navigate from one end of the tunnel to the other as quickly as possible, without touching the boundaries of the tunnel. A real world example that approximates this task is driving a car down a road that may have twists and turns, where the car must navigate the road as quickly as possible without touching the sides of the road. The steering law predicts both the instantaneous speed at which we may navigate the tunnel, and the total time required to navigate the entire tunnel.
The steering law has been independently discovered and studied three times (Rashevsky, 1959; Drury, 1971; Accot and Zhai, 1997). Its most recent discovery has been within the human-computer interaction community, which has resulted in the most general mathematical formulation of the law.
and ah-koh in French
). In this context, the steering law is a predictive model of human movement
, concerning the speed and total time with which a user may steer a pointing device
(such as a mouse or stylus
) through a 2D tunnel presented on a screen (i.e. with a bird's eye view of the tunnel), where the user must travel from one end of the path to the other as quickly as possible, while staying within the confines of the path. One potential practical application of this law is in modelling a user's performance in navigating a hierarchical cascading menu
.
Many researchers in human-computer interaction, including Accot himself, find it surprising or even amazing that the steering law model predicts performance as well as it does, given the almost purely mathematical way in which it was derived. Some consider this a testament to the robustness of Fitts's law.
In its general form, the steering law can be expressed as
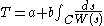
where T is the average time to navigate through the path, C is the path parameterized by s, W(s) is the width of the path at s, and a and b are experimentally fitted constants. In general, the path may have a complicated curvilinear shape (such as a spiral) with variable thickness W(s).
Simpler paths allow for mathematical simplifications of the general form of the law. For example, if the path is a straight tunnel of constant width W, the equation reduces to
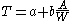
where A is the length of the path. We see, especially in this simplified form, a speed-accuracy tradeoff, somewhat similar to that in Fitts's law.
We can also differentiate both sides of the integral equation with respect to s to obtain the local, or instantaneous, form of the law:
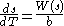
which says that the instantaneous speed of the user is proportional to the width of the tunnel. This makes intuitive sense if we consider the analogous task of driving a car down a road: the wider the road, the faster we can drive and still stay on the road, even if there are curves in the road.
Assume that the time required for goal passing (i.e. passing a pointer through a goal at distance A and of width W,
oriented perpendicular to the axis of motion) can be modeled with this form of Fitts's law:

Then, a straight tunnel of length A and constant width W can be approximated as a sequence of N evenly spaced goals, each separated from its neighbours by a distance of A/N. We can let N grow arbitrarily large, making the distance between successive goals become infinitesimal. The total time to navigative through all the goals, and thus through the tunnel, is
Next, consider a curved tunnel of total length A, parameterized by s varying from 0 to A. Let W(s) be the variable width of the tunnel. The tunnel can be approximated as a sequence of N straight tunnels, numbered 1 through N, each located at si where i = 1 to N, and each of length si+1 − si and of width W(si). We can let N grow arbitrarily large, making the length of successive straight tunnels become infinitesimal. The total time to navigative through the curved tunnel is
yielding the general form of the steering law.
Human–computer interaction
Human–computer Interaction is the study, planning, and design of the interaction between people and computers. It is often regarded as the intersection of computer science, behavioral sciences, design and several other fields of study...
and ergonomics
Ergonomics
Ergonomics is the study of designing equipment and devices that fit the human body, its movements, and its cognitive abilities.The International Ergonomics Association defines ergonomics as follows:...
is a predictive model of human movement that describes the time required to navigate, or steer, through a 2-dimensional tunnel. The tunnel can be thought of as a path or trajectory on a plane that has an associated thickness or width, where the width can vary along the tunnel. The goal of a steering task is to navigate from one end of the tunnel to the other as quickly as possible, without touching the boundaries of the tunnel. A real world example that approximates this task is driving a car down a road that may have twists and turns, where the car must navigate the road as quickly as possible without touching the sides of the road. The steering law predicts both the instantaneous speed at which we may navigate the tunnel, and the total time required to navigate the entire tunnel.
The steering law has been independently discovered and studied three times (Rashevsky, 1959; Drury, 1971; Accot and Zhai, 1997). Its most recent discovery has been within the human-computer interaction community, which has resulted in the most general mathematical formulation of the law.
The steering law in human-computer interaction
Within human-computer interaction, the law was rediscovered by Johnny Accot and Shumin Zhai, who mathematically derived it in a novel way from Fitts's law using integral calculus, experimentally verified it for a class of tasks, and developed the most general mathematical statement of it. Some researchers within this community have sometimes referred to the law as the Accot-Zhai steering law or Accot's law (Accot is pronounced ah-cot in EnglishEnglish language
English is a West Germanic language that arose in the Anglo-Saxon kingdoms of England and spread into what was to become south-east Scotland under the influence of the Anglian medieval kingdom of Northumbria...
and ah-koh in French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
). In this context, the steering law is a predictive model of human movement
Locomotor system
Locomotor system may mean:* Animal locomotion system* Human musculoskeletal system, also known simply as "the locomotor system"...
, concerning the speed and total time with which a user may steer a pointing device
Pointing device
A pointing device is an input interface that allows a user to input spatial data to a computer...
(such as a mouse or stylus
Stylus
A stylus is a writing utensil, or a small tool for some other form of marking or shaping, for example in pottery. The word is also used for a computer accessory . It usually refers to a narrow elongated staff, similar to a modern ballpoint pen. Many styli are heavily curved to be held more easily...
) through a 2D tunnel presented on a screen (i.e. with a bird's eye view of the tunnel), where the user must travel from one end of the path to the other as quickly as possible, while staying within the confines of the path. One potential practical application of this law is in modelling a user's performance in navigating a hierarchical cascading menu
Menu (computing)
In computing and telecommunications, a menu is a list of commands presented to an operator by a computer or communications system. A menu is used in contrast to a command-line interface, where instructions to the computer are given in the form of commands .Choices given from a menu may be selected...
.
Many researchers in human-computer interaction, including Accot himself, find it surprising or even amazing that the steering law model predicts performance as well as it does, given the almost purely mathematical way in which it was derived. Some consider this a testament to the robustness of Fitts's law.
In its general form, the steering law can be expressed as
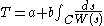
where T is the average time to navigate through the path, C is the path parameterized by s, W(s) is the width of the path at s, and a and b are experimentally fitted constants. In general, the path may have a complicated curvilinear shape (such as a spiral) with variable thickness W(s).
Simpler paths allow for mathematical simplifications of the general form of the law. For example, if the path is a straight tunnel of constant width W, the equation reduces to
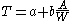
where A is the length of the path. We see, especially in this simplified form, a speed-accuracy tradeoff, somewhat similar to that in Fitts's law.
We can also differentiate both sides of the integral equation with respect to s to obtain the local, or instantaneous, form of the law:
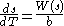
which says that the instantaneous speed of the user is proportional to the width of the tunnel. This makes intuitive sense if we consider the analogous task of driving a car down a road: the wider the road, the faster we can drive and still stay on the road, even if there are curves in the road.
Derivation of the model from Fitts's law
This derivation is only meant as a high level sketch. It lacks the illustrations of, and may differ in detail from, the derivation given by Accot and Zhai (1997).Assume that the time required for goal passing (i.e. passing a pointer through a goal at distance A and of width W,
oriented perpendicular to the axis of motion) can be modeled with this form of Fitts's law:

Then, a straight tunnel of length A and constant width W can be approximated as a sequence of N evenly spaced goals, each separated from its neighbours by a distance of A/N. We can let N grow arbitrarily large, making the distance between successive goals become infinitesimal. The total time to navigative through all the goals, and thus through the tunnel, is
| Tstraight tunnel | 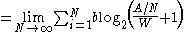 |
|
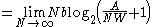 |
||
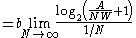 |
(applying L'Hôpital's rule L'Hôpital's rule In calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit... ...) |
|
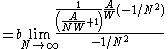 |
||
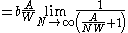 |
||
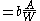 |
Next, consider a curved tunnel of total length A, parameterized by s varying from 0 to A. Let W(s) be the variable width of the tunnel. The tunnel can be approximated as a sequence of N straight tunnels, numbered 1 through N, each located at si where i = 1 to N, and each of length si+1 − si and of width W(si). We can let N grow arbitrarily large, making the length of successive straight tunnels become infinitesimal. The total time to navigative through the curved tunnel is
| Tcurved tunnel | 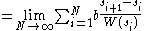 |
|
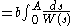 |
(... by the definition of the definite integral Integral Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus... ) |
yielding the general form of the steering law.
Modeling steering in layers
Steering law has been extended to predict movement time for steering in layers of thickness t. The relation is given bySee also
- Crossing-based interface — any graphical user interface that uses goal crossing tasks as the basic interaction paradigm