
Ackermann set theory
Encyclopedia
Ackermann set theory is a version of axiomatic set theory proposed by Wilhelm Ackermann
in 1956.
. The language consists of one binary relation
consists of one binary relation  and one constant
and one constant 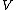 (Ackermann used a predicate
(Ackermann used a predicate  instead). We will write
instead). We will write 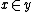 for
for 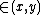 . The intended interpretation of
. The intended interpretation of 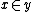 is that the object
is that the object  is in the class
is in the class 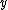 . The intended interpretation of
. The intended interpretation of  is the class of all sets.
is the class of all sets.
1) Axiom of extensionality
: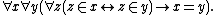
2) Class construction axiom schema: Let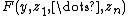 be any formula which does not contain the variable
be any formula which does not contain the variable  free.
free.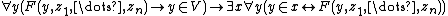
3) Reflection axiom schema: Let be any formula which does not contain the constant symbol
be any formula which does not contain the constant symbol 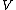 or the variable
or the variable  free. If
free. If 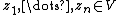 then
then
4) Completeness axioms for
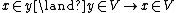
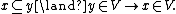
5) Axiom of regularity for sets
: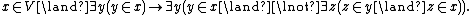
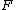 be a first-order formula
be a first-order formula
in the language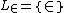 (so
(so 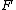 does not contain the constant
does not contain the constant  ). Define the "restriction of
). Define the "restriction of  to the universe of sets" (denoted
to the universe of sets" (denoted 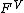 ) to be the formula which is obtained by recursively replacing all sub-formulas of
) to be the formula which is obtained by recursively replacing all sub-formulas of 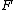 of the form
of the form 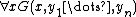 with
with 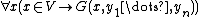 and all sub-formulas of the form
and all sub-formulas of the form 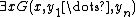 with
with 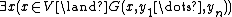 .
.
In 1959 Azriel Levy
proved that if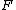 is a formula of
is a formula of  and A proves
and A proves 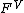 , then ZF
, then ZF
proves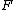
In 1970 William Reinhardt proved that if is a formula of
is a formula of 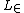 and ZF proves
and ZF proves 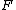 , then A proves
, then A proves  .
.
Wilhelm Ackermann
Wilhelm Friedrich Ackermann was a German mathematician best known for the Ackermann function, an important example in the theory of computation....
in 1956.
The language
Ackermann set theory is formulated in first-order logicFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. The language
 consists of one binary relation
consists of one binary relation  and one constant
and one constant 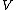 (Ackermann used a predicate
(Ackermann used a predicate  instead). We will write
instead). We will write 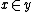 for
for 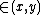 . The intended interpretation of
. The intended interpretation of 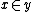 is that the object
is that the object  is in the class
is in the class 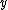 . The intended interpretation of
. The intended interpretation of  is the class of all sets.
is the class of all sets.The axioms
The axioms of Ackermann set theory, collectively referred to as A, consists of the universal closure of the following formulas in the language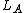
1) Axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
:
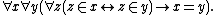
2) Class construction axiom schema: Let
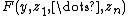 be any formula which does not contain the variable
be any formula which does not contain the variable  free.
free.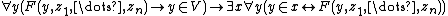
3) Reflection axiom schema: Let
 be any formula which does not contain the constant symbol
be any formula which does not contain the constant symbol 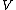 or the variable
or the variable  free. If
free. If 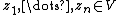 then
then
4) Completeness axioms for

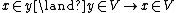
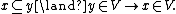
5) Axiom of regularity for sets
Axiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
:
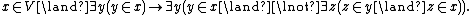
Relation to Zermelo–Fraenkel set theory
Let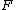 be a first-order formula
be a first-order formulaFirst-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
in the language
 (so
(so 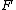 does not contain the constant
does not contain the constant  ). Define the "restriction of
). Define the "restriction of  to the universe of sets" (denoted
to the universe of sets" (denoted 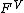 ) to be the formula which is obtained by recursively replacing all sub-formulas of
) to be the formula which is obtained by recursively replacing all sub-formulas of 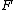 of the form
of the form 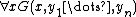 with
with 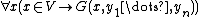 and all sub-formulas of the form
and all sub-formulas of the form 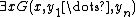 with
with 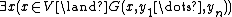 .
.In 1959 Azriel Levy
Azriel Levy
Azriel Levy is an Israeli mathematician, logician, and a professor emeritus at the Hebrew University of Jerusalem....
proved that if
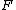 is a formula of
is a formula of  and A proves
and A proves 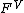 , then ZF
, then ZFZermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
proves
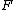
In 1970 William Reinhardt proved that if
 is a formula of
is a formula of 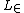 and ZF proves
and ZF proves 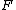 , then A proves
, then A proves  .
.

