Acoustic metric
Encyclopedia
In mathematical physics
, a metric
describes the arrangement of relative distances within a surface or volume, usually measured by signals passing through the region – essentially describing the intrinsic geometry of the region. An acoustic metric will describe the signal-carrying properties characteristic of a given particulate medium in acoustics
, or in fluid dynamics
. Other descriptive names such as sonic metric are also sometimes used, interchangeably.
, and that this space is filled with an isotropic inviscid fluid at zero temperature (e.g. a superfluid
). This fluid is described by a density field ρ and a velocity field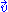
. The speed of sound at any given point depends upon the compressibility which in turn depends upon the density at that point. This can be specified by the "speed of sound field" c. Now, the combination of both isotropy and Galilean covariance tells us that the permissible velocities of the sound waves at a given point x, 
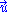has to satisfy
This restriction can also arise if we imagine that sound is like "light" moving though a spacetime described by an effective metric tensor
called the acoustic metric.
The acoustic metric
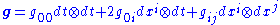
"Light" moving with a velocity of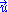
(NOT the 4-velocity) has to satisfy
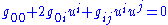
If
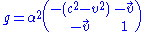
where α is some conformal factor which is yet to be determined (see Weyl rescaling), we get the desired velocity restriction. α may be some function of the density, for example.
), these metrics have sometimes been studied in the hope that they might shed light on the statistical mechanics
of actual black holes. Some people have suggested that analog models are more than just an analogy and that the actual gravity that we observe is actually an analog theory. But in order for this to hold, since a generic analog model depends upon BOTH the acoustic metric AND the underlying background geometry, the low energy large wavelength limit of the theory has to decouple from the background geometry.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
describes the arrangement of relative distances within a surface or volume, usually measured by signals passing through the region – essentially describing the intrinsic geometry of the region. An acoustic metric will describe the signal-carrying properties characteristic of a given particulate medium in acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
, or in fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
. Other descriptive names such as sonic metric are also sometimes used, interchangeably.
A simple fluid example
For simplicity, we will assume that the underlying background geometry is EuclideanEuclidean
Euclidean relates to Euclid , a town or others. It may refer to:Geometry...
, and that this space is filled with an isotropic inviscid fluid at zero temperature (e.g. a superfluid
Superfluid
Superfluidity is a state of matter in which the matter behaves like a fluid without viscosity and with extremely high thermal conductivity. The substance, which appears to be a normal liquid, will flow without friction past any surface, which allows it to continue to circulate over obstructions and...
). This fluid is described by a density field ρ and a velocity field
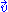. The speed of sound at any given point depends upon the compressibility which in turn depends upon the density at that point. This can be specified by the "speed of sound field" c. Now, the combination of both isotropy and Galilean covariance tells us that the permissible velocities of the sound waves at a given point x, 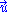has to satisfyThis restriction can also arise if we imagine that sound is like "light" moving though a spacetime described by an effective metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
called the acoustic metric.
The acoustic metric
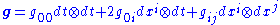
"Light" moving with a velocity of
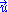(NOT the 4-velocity) has to satisfy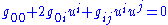If
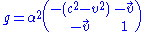
where α is some conformal factor which is yet to be determined (see Weyl rescaling), we get the desired velocity restriction. α may be some function of the density, for example.
Acoustic horizons
An acoustic metric can give rise to "acoustic horizons" (also known as "sonic horizons"), analogous to the event horizons in the spacetime metric of general relativity. However, unlike the spacetime metric, in which the invariant speed is the absolute upper limit on the propagation of all causal effects, the invariant speed in an acoustic metric is not the upper limit on propagation speeds. For example, the speed of sound is less than the speed of light. As a result, the horizons in acoustic metrics are not perfectly analogous to those associated with the spacetime metric. It is possible for certain physical effects to propagate back across an acoustic horizon. Such propagation is sometimes considered to be analogous to Hawking radiation, although the latter arises from quantum field effects in curved spacetime.Acoustic metrics and quantum gravity
Since acoustic metrics share some statistical behaviours with the way that we expect a future theory of quantum gravity to behave (such as Hawking radiationHawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
), these metrics have sometimes been studied in the hope that they might shed light on the statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
of actual black holes. Some people have suggested that analog models are more than just an analogy and that the actual gravity that we observe is actually an analog theory. But in order for this to hold, since a generic analog model depends upon BOTH the acoustic metric AND the underlying background geometry, the low energy large wavelength limit of the theory has to decouple from the background geometry.
See also
- Analog models of gravityAnalog models of gravityAnalogue models of gravity is a direction of research in physics, where various phenomena of general relativity are modeled by other physical systems, such as acoustics in a moving fluid, superfluid helium, or Bose-Einstein condensate; gravity waves in water; and propagation of electromagnetic...
- Hawking radiationHawking radiationHawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
- gravastarGravastarA gravastar is an object hypothesized in astrophysics as an alternative to the black hole theory by Pawel Mazur and Emil Mottola. It results from assuming real, physical limitations on the formation of black holes...
- acousticsAcousticsAcoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
- metric (mathematics)Metric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
- quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
- quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...