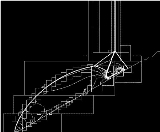
Adaptive mesh refinement
Encyclopedia
In numerical analysis
, adaptive mesh refinement is a method of adaptive meshing. Central to any Eulerian method is the manner in which it discretizes the continuous domain of interest into a grid of many individual elements. This grid may be static, established once and for all at the beginning of the computation, or it may be dynamic, tracking the features of the result as the computation progresses. If the computation has features which one wants to track which are much smaller than the overall scale of the problem, and which move in time, then one must either include many more static grids to cover the region of interest, or adopt a dynamic scheme.
The advantages of a dynamic gridding scheme are:
 In a series of papers, Marsha Berger, Joseph Oliger, and Phillip Colella
In a series of papers, Marsha Berger, Joseph Oliger, and Phillip Colella
developed an algorithm
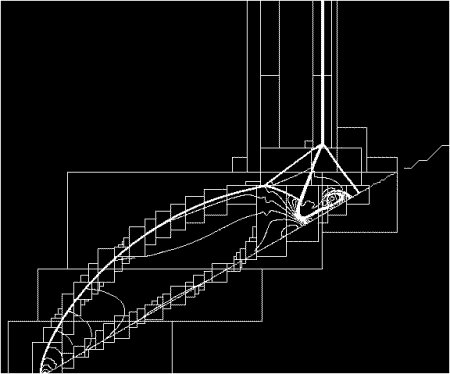
for dynamic gridding called local adaptive mesh refinement. The algorithm begins with the entire computational domain
covered with a coarsely resolved base-level regular Cartesian grid
. As the calculation progresses, individual grid cells are tagged for refinement, using a criterion that can either be user-supplied (for example mass
per cell remains constant, hence higher density
regions are more highly resolved) or based on Richardson extrapolation
.
All tagged cells are then refined, meaning that a finer grid is overlaid on the coarse one. After refinement, individual grid patches on a single fixed level of refinement are passed off to an integrator
which advances those cells in time
. Finally, a correction procedure is implemented to correct the transfer along coarse-fine grid interfaces, to ensure that the amount of any conserved quantity leaving one cell exactly balances the amount entering the bordering cell. If at some point the level of refinement in a cell is greater than required, the high resolution grid may be removed and replaced with a coarser grid.
This allows the user to solve problems that are completely intractable on a uniform grid
; for example, astrophysicists
have used AMR to model a collapsing giant molecular cloud core down to an effective resolution of 131,072 cells per initial cloud radius
, corresponding to a resolution of 1015 cells on a uniform grid.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, adaptive mesh refinement is a method of adaptive meshing. Central to any Eulerian method is the manner in which it discretizes the continuous domain of interest into a grid of many individual elements. This grid may be static, established once and for all at the beginning of the computation, or it may be dynamic, tracking the features of the result as the computation progresses. If the computation has features which one wants to track which are much smaller than the overall scale of the problem, and which move in time, then one must either include many more static grids to cover the region of interest, or adopt a dynamic scheme.
The advantages of a dynamic gridding scheme are:
- Increased computational savings over a static grid approach.
- Increased storage savings over a static grid approach.
- Complete control of grid resolution, compared to the fixed resolution of a static grid approach, or the Lagrangian-based adaptivity of smoothed particle hydrodynamicsSmoothed particle hydrodynamicsSmoothed-particle hydrodynamics is a computational method used for simulating fluid flows. It has been used in many fields of research, including astrophysics, ballistics, volcanology, and oceanography...
.
Introduction to adaptive mesh refinement

Phillip Colella
Phillip Colella is an American applied mathematician and the Head of the Applied Numerical Algorithms Group at the National Energy Research Scientific Computing Center, Lawrence Berkeley National Laboratory. He has also worked at Lawrence Livermore National Laboratory...
developed an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for dynamic gridding called local adaptive mesh refinement. The algorithm begins with the entire computational domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
covered with a coarsely resolved base-level regular Cartesian grid
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
. As the calculation progresses, individual grid cells are tagged for refinement, using a criterion that can either be user-supplied (for example mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
per cell remains constant, hence higher density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
regions are more highly resolved) or based on Richardson extrapolation
Richardson extrapolation
In numerical analysis, Richardson extrapolation is a sequence acceleration method, used to improve the rate of convergence of a sequence. It is named after Lewis Fry Richardson, who introduced the technique in the early 20th century. In the words of Birkhoff and Rota, ".....
.
All tagged cells are then refined, meaning that a finer grid is overlaid on the coarse one. After refinement, individual grid patches on a single fixed level of refinement are passed off to an integrator
Integrator
An integrator is a device to perform the mathematical operation known as integration, a fundamental operation in calculus.The integration function is often part of engineering, physics, mechanical, chemical and scientific calculations....
which advances those cells in time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
. Finally, a correction procedure is implemented to correct the transfer along coarse-fine grid interfaces, to ensure that the amount of any conserved quantity leaving one cell exactly balances the amount entering the bordering cell. If at some point the level of refinement in a cell is greater than required, the high resolution grid may be removed and replaced with a coarser grid.
This allows the user to solve problems that are completely intractable on a uniform grid
Regular grid
A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes . Grids of this type appear on graph paper and may be used in finite element analysis as well as finite volume methods and finite difference methods...
; for example, astrophysicists
Astrophysics
Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...
have used AMR to model a collapsing giant molecular cloud core down to an effective resolution of 131,072 cells per initial cloud radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
, corresponding to a resolution of 1015 cells on a uniform grid.
See also
- Adaptive stepsizeAdaptive stepsizeAdaptive stepsize is a technique in numerical analysis used for many problems, but mainly for integration. It can be used for both normal integration , or the process of solving an ordinary differential equation. This article focuses on the latter...
- Cactus FrameworkCactus FrameworkCactus is an open-source, problem-solving environment designed for scientists and engineers. Its modular structure easily enables parallel computation across different architectures and collaborative code development between different groups...
- Multigrid methodMultigrid methodMultigrid methods in numerical analysis are a group of algorithms for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior...
- Silo (library)Silo (library)Silo is a computer data format and library developed at Lawrence Livermore National Laboratory for storing rectilinear, curvilinear, unstructured, or point meshes in 2D and 3D. It supports data upon those meshes, including scalar, vector, and tensor variables; volume fraction-based materials; and...

