Smoothed particle hydrodynamics
Encyclopedia
Smoothed-particle hydrodynamics (SPH) is a computational method used for simulating fluid
flows. It has been used in many fields of research, including astrophysics
, ballistics
, volcanology
, and oceanography
. It is a mesh-free Lagrangian method (where the coordinates move with the fluid), and the resolution of the method can easily be adjusted with respect to variables such as the density
.
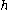), over which their properties are "smoothed" by a kernel function
. This means that the physical quantity of any particle can be obtained by summing the relevant properties of all the particles which lie within the range of the kernel. For example, using Monaghan's popular cubic spline kernel the temperature
at position
depends on the temperatures of all the particles within a radial distance 
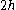of 
.
The contributions of each particle to a property are weighted according to their distance from the particle of interest, and their density. Mathematically, this is governed by the kernel function (symbol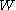
). Kernel functions commonly used include the Gaussian function and the cubic spline. The latter function is exactly zero for particles further away than two smoothing lengths (unlike the Gaussian, where there is a small contribution at any finite distance away). This has the advantage of saving computational effort by not including the relatively minor contributions from distant particles.
The equation for any quantity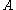
at any point 
is given by the equation
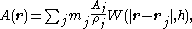
where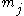
is the mass
of particle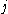
, 
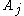is the value of the quantity 
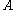for particle 
, 
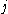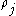is the density
associated with particle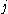
, 
denotes position and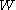 
is the kernel function mentioned above. For example, the density of particle 
(
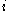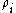) can be expressed as:
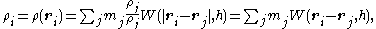
where the summation over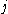
includes all particles in the simulation.
Similarly, the spatial derivative of a quantity can be obtained by using integration by parts
to shift the del
(
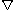) operator from the physical quantity to the kernel function,
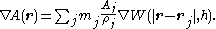
Although the size of the smoothing length can be fixed in both space
and time
, this does not take advantage of the full power of SPH. By assigning each particle its own smoothing length and allowing it to vary with time, the resolution of a simulation can be made to automatically adapt itself depending on local conditions. For example, in a very dense region where many particles are close together the smoothing length can be made relatively short, yielding high spatial resolution. Conversely, in low-density regions where individual particles are far apart and the resolution is low, the smoothing length can be increased, optimising the computation for the regions of interest. Combined with an equation of state
and an integrator
, SPH can simulate hydrodynamic flows efficiently. However, the traditional artificial viscosity formulation used in SPH tends to smear out shocks
and contact discontinuities to a much greater extent than state-of-the-art grid-based schemes.
The Lagrangian-based adaptivity of SPH is analogous to the adaptivity present in grid-based adaptive mesh refinement
codes, though in the latter case one can refine the mesh spacing according to any criterion selected by the user. Because it is Lagrangian in nature, SPH is limited to refining based on density alone.
Often in astrophysics, one wishes to model self-gravity in addition to pure hydrodynamics. The particle-based nature of SPH makes it ideal to combine with a particle-based gravity solver, for instance tree gravity, particle mesh
, or particle-particle particle-mesh
.
, make it ideal for computations in theoretical astrophysics.
Simulations of galaxy formation, star formation
, stellar collisions, supernovae and meteor
impacts are some of the wide variety of astrophysical and cosmological uses of this method.
SPH is used to model hydrodynamic flows, including possible effects of gravity. Incorporating other astrophysical processes which may be important, such as radiative transfer
and magnetic fields
is an active area of research in the astronomical community, and has had some limited success. http://www.astro.ex.ac.uk/people/mbate/Cluster/clusterRT.html
Smoothed-particle hydrodynamics is being increasingly used to model fluid motion as well. This is due to several benefits over traditional grid-based techniques. First, SPH guarantees conservation of mass without extra computation since the particles themselves represent mass. Second, SPH computes pressure from weighted contributions of neighboring particles rather than by solving linear systems of equations. Finally, unlike grid-base technique which must track fluid boundaries, SPH creates a free surface for two-phase interacting fluids directly since the particles represent the denser fluid (usually water) and empty space represents the lighter fluid (usually air). For these reasons it is possible to simulate fluid motion using SPH in real time. However, both grid-based and SPH techniques still require the generation of renderable free surface geometry using a polygonization technique such as metaballs
and marching cubes
, point splatting, or "carpet" visualization. For gas dynamics it is more appropriate to use the kernel function itself to produce a rendering of gas column density (e.g. as done in the SPLASH visualisation package).
One drawback over grid-based techniques is the need for large numbers of particles to produce simulations of equivalent resolution. In the typical implementation of both uniform grids and SPH particle techniques, many voxels or particles will be used to fill water volumes which are never rendered. However, accuracy can be significantly higher with sophisticated grid-based techniques, especially those coupled with particle methods (such as particle level sets), since it is easier to enforce the incompressibility condition in these systems. SPH for fluid simulation is being used increasingly in real-time animation and games where accuracy is not as critical as interactivity.
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
flows. It has been used in many fields of research, including astrophysics
Astrophysics
Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...
, ballistics
Ballistics
Ballistics is the science of mechanics that deals with the flight, behavior, and effects of projectiles, especially bullets, gravity bombs, rockets, or the like; the science or art of designing and accelerating projectiles so as to achieve a desired performance.A ballistic body is a body which is...
, volcanology
Volcanology
Volcanology is the study of volcanoes, lava, magma, and related geological, geophysical and geochemical phenomena. The term volcanology is derived from the Latin word vulcan. Vulcan was the ancient Roman god of fire....
, and oceanography
Oceanography
Oceanography , also called oceanology or marine science, is the branch of Earth science that studies the ocean...
. It is a mesh-free Lagrangian method (where the coordinates move with the fluid), and the resolution of the method can easily be adjusted with respect to variables such as the density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
.
Method
The smoothed-particle hydrodynamics (SPH) method works by dividing the fluid into a set of discrete elements, referred to as particles. These particles have a spatial distance (known as the "smoothing length", typically represented in equations by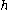), over which their properties are "smoothed" by a kernel functionKernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
. This means that the physical quantity of any particle can be obtained by summing the relevant properties of all the particles which lie within the range of the kernel. For example, using Monaghan's popular cubic spline kernel the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
at position
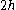depends on the temperatures of all the particles within a radial distance of .The contributions of each particle to a property are weighted according to their distance from the particle of interest, and their density. Mathematically, this is governed by the kernel function (symbol
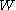). Kernel functions commonly used include the Gaussian function and the cubic spline. The latter function is exactly zero for particles further away than two smoothing lengths (unlike the Gaussian, where there is a small contribution at any finite distance away). This has the advantage of saving computational effort by not including the relatively minor contributions from distant particles.The equation for any quantity
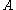at any point is given by the equation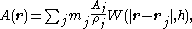where
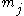is the massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of particle
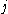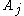, is the value of the quantity 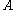for particle 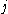, 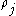is the densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
associated with particle
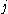, denotes position and 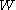is the kernel function mentioned above. For example, the density of particle 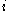(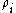) can be expressed as: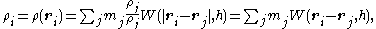where the summation over
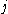includes all particles in the simulation.Similarly, the spatial derivative of a quantity can be obtained by using integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
to shift the del
Del
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
(
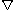) operator from the physical quantity to the kernel function,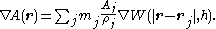Although the size of the smoothing length can be fixed in both space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, this does not take advantage of the full power of SPH. By assigning each particle its own smoothing length and allowing it to vary with time, the resolution of a simulation can be made to automatically adapt itself depending on local conditions. For example, in a very dense region where many particles are close together the smoothing length can be made relatively short, yielding high spatial resolution. Conversely, in low-density regions where individual particles are far apart and the resolution is low, the smoothing length can be increased, optimising the computation for the regions of interest. Combined with an equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
and an integrator
Integrator
An integrator is a device to perform the mathematical operation known as integration, a fundamental operation in calculus.The integration function is often part of engineering, physics, mechanical, chemical and scientific calculations....
, SPH can simulate hydrodynamic flows efficiently. However, the traditional artificial viscosity formulation used in SPH tends to smear out shocks
Shock wave
A shock wave is a type of propagating disturbance. Like an ordinary wave, it carries energy and can propagate through a medium or in some cases in the absence of a material medium, through a field such as the electromagnetic field...
and contact discontinuities to a much greater extent than state-of-the-art grid-based schemes.
The Lagrangian-based adaptivity of SPH is analogous to the adaptivity present in grid-based adaptive mesh refinement
Adaptive mesh refinement
In numerical analysis, adaptive mesh refinement is a method of adaptive meshing. Central to any Eulerian method is the manner in which it discretizes the continuous domain of interest into a grid of many individual elements...
codes, though in the latter case one can refine the mesh spacing according to any criterion selected by the user. Because it is Lagrangian in nature, SPH is limited to refining based on density alone.
Often in astrophysics, one wishes to model self-gravity in addition to pure hydrodynamics. The particle-based nature of SPH makes it ideal to combine with a particle-based gravity solver, for instance tree gravity, particle mesh
Particle Mesh
Particle Mesh is a computational method for determining the forces in a system of particles. These particles could be atoms, stars, or fluid components and so the method is applicable to many fields, including molecular dynamics and astrophysics. The basic principle is that a system of particles...
, or particle-particle particle-mesh
P3M
Particle-Particle-Particle Mesh is a Fourier-based Ewald summation method to calculate potentials in N-body simulations.The potential could be the electrostatic potential among N point charges i.e. molecular dynamics, the gravitational potential among N gas particles in e.g. smoothed particle...
.
Uses in astrophysics
The adaptive resolution of smoothed-particle hydrodynamics, combined with its ability to simulate phenomena covering many orders of magnitudeOrder of magnitude
An order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount being scaled is 10 and the scale is the exponent being applied to this amount...
, make it ideal for computations in theoretical astrophysics.
Simulations of galaxy formation, star formation
Star formation
Star formation is the process by which dense parts of molecular clouds collapse into a ball of plasma to form a star. As a branch of astronomy star formation includes the study of the interstellar medium and giant molecular clouds as precursors to the star formation process and the study of young...
, stellar collisions, supernovae and meteor
METEOR
METEOR is a metric for the evaluation of machine translation output. The metric is based on the harmonic mean of unigram precision and recall, with recall weighted higher than precision...
impacts are some of the wide variety of astrophysical and cosmological uses of this method.
SPH is used to model hydrodynamic flows, including possible effects of gravity. Incorporating other astrophysical processes which may be important, such as radiative transfer
Radiative transfer
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission and scattering processes. The equation of radiative transfer describes these interactions mathematically...
and magnetic fields
Magnetohydrodynamics
Magnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes...
is an active area of research in the astronomical community, and has had some limited success. http://www.astro.ex.ac.uk/people/mbate/Cluster/clusterRT.html
Uses in fluid simulation
Metaballs
Metaballs are, in computer graphics, organic-looking n-dimensional objects. The technique for rendering metaballs was invented by Jim Blinn in the early 1980s....
and marching cubes
Marching cubes
Marching cubes is a computer graphics algorithm, published in the 1987 SIGGRAPH proceedings by Lorensen and Cline, for extracting a polygonal mesh of an isosurface from a three-dimensional scalar field...
, point splatting, or "carpet" visualization. For gas dynamics it is more appropriate to use the kernel function itself to produce a rendering of gas column density (e.g. as done in the SPLASH visualisation package).
One drawback over grid-based techniques is the need for large numbers of particles to produce simulations of equivalent resolution. In the typical implementation of both uniform grids and SPH particle techniques, many voxels or particles will be used to fill water volumes which are never rendered. However, accuracy can be significantly higher with sophisticated grid-based techniques, especially those coupled with particle methods (such as particle level sets), since it is easier to enforce the incompressibility condition in these systems. SPH for fluid simulation is being used increasingly in real-time animation and games where accuracy is not as critical as interactivity.
Uses in solid mechanics
William G. Hoover has used SPH to study impact fracture in solids. Hoover and others use the acronym SPAM (smooth-particle applied mechanics) to refer to the numerical method. The application of smoothed-particle methods to solid mechanics remains a relatively unexplored field.External links
- First large simulation of star formation using SPH
- SPHERIC (SPH European Research Interest Community)
- ITVO is the web-site of The Italian Theoretical Virtual Observatory created to query a database of numerical simulation archive.
- SPHC Image Gallery depicts a wide variety of test cases, experimental validations, and commercial applications of the SPH code SPHC.
Software
- Algodoo is a 2D simulation framework for education using SPH
- SPH-flow
- FLUIDS v.1 is a simple, open source (Zlib), real-time 3D SPH implementation in C++ for liquids for CPU and GPU.
- GADGETGADGETGADGET is a freely available code for cosmological N-body/SPH simulations written by Volker Springel at the Max Planck Institute for Astrophysics...
is a freely available (GPL) code for cosmological N-body/SPH simulations - ISPH parallel C++/OpenCL open source truly incompressible SPH implementation
- SimPARTIX is a commercial simulation package for SPH and DEM simulations from Fraunhofer IWM
- SPLASH is an open source (GPL) visualisation tool for SPH simulations
- SPHysics is an open source SPH implementation in Fortran
- DualSPHysics is a package of executables based on SPHysics and using GPU computing
- Physics Abstraction Layer is an open source abstraction system that supports real time physics engines with SPH support
- Pasimodo is a program package for particle-based simulation methods, e.g. SPH
- Punto is a freely available visualisation tool for particle simulations
- GPUSPH SPH simulator with viscosity (GPLv3)