
Adequality
Encyclopedia
In the history of infinitesimal calculus
, adequality is a technique developed by Pierre de Fermat
. Fermat said he borrowed the term from Diophantus
. Adequality was a technique first used to find maxima for functions and then adapted to find tangent lines to curves. The term adequality has been interpreted by some authors to mean approximate equality, but as mentioned below there is considerable disagreement amongst scholars as to the exact meaning. To find the maximum of a function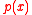 , Fermat would equate (or more precisely adequate)
, Fermat would equate (or more precisely adequate) 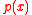 and
and  and after doing algebra he could divide by e, and then discard any remaining terms involving e. To use Fermat's own example to illustrate the method, consider the problem of finding the maximum of
and after doing algebra he could divide by e, and then discard any remaining terms involving e. To use Fermat's own example to illustrate the method, consider the problem of finding the maximum of  . Fermat adequated
. Fermat adequated  with
with 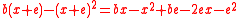 . That is (using the notation
. That is (using the notation  to denote adequality):
to denote adequality):
Canceling terms and dividing by Fermat arrived at
Fermat arrived at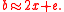
Removing the terms that contained Fermat arrived at the desired result that the maximum occurred when
Fermat arrived at the desired result that the maximum occurred when 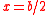 .
.
, and Descartes was quite proud of his discovery. He also notes that while Fermat's methods were closer to the future developments in calculus, Descartes methods had a more immediate impact on the development.
ever lifted up his pen to write The Analyst
.
Regardless of whether or not his work is viewed today as infinitesimal calculus his method yielded results that were far from trivial. Grabiner writes that he used his principle to give a mathematical derivation of Snell's laws of refraction directly from the principle that light takes the quickest path.
Infinitesimal calculus
Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
, adequality is a technique developed by Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
. Fermat said he borrowed the term from Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
. Adequality was a technique first used to find maxima for functions and then adapted to find tangent lines to curves. The term adequality has been interpreted by some authors to mean approximate equality, but as mentioned below there is considerable disagreement amongst scholars as to the exact meaning. To find the maximum of a function
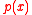 , Fermat would equate (or more precisely adequate)
, Fermat would equate (or more precisely adequate) 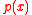 and
and  and after doing algebra he could divide by e, and then discard any remaining terms involving e. To use Fermat's own example to illustrate the method, consider the problem of finding the maximum of
and after doing algebra he could divide by e, and then discard any remaining terms involving e. To use Fermat's own example to illustrate the method, consider the problem of finding the maximum of  . Fermat adequated
. Fermat adequated  with
with 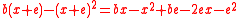 . That is (using the notation
. That is (using the notation  to denote adequality):
to denote adequality):
Canceling terms and dividing by
 Fermat arrived at
Fermat arrived at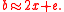
Removing the terms that contained
 Fermat arrived at the desired result that the maximum occurred when
Fermat arrived at the desired result that the maximum occurred when 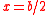 .
.Descartes' criticism
Fermat's method was highly criticized by his contemporaries, particularly Descartes. V. Katz suggests this is because Descartes had independently discovered the same new mathematics, known as his method of normalsMethod of normals
In calculus, the method of normals was a technique invented by Descartes for finding normal and tangent lines to curves. It represented one of the earliest methods for constructing tangents to curves. The method hinges on the observation that the radius of a circle is always normal to the...
, and Descartes was quite proud of his discovery. He also notes that while Fermat's methods were closer to the future developments in calculus, Descartes methods had a more immediate impact on the development.
Scholarly controversy
There is disagreement amongst scholars about the exact meaning of Fermat's adequality. Edwards explains this is because Fermat never described his method with sufficient clarity of completeness to determine precisely what he intended. Fermat never explained if e was supposed to be taken to be small, infinitesimal, or if he was taking a limit. Depending on how one reads into Fermat's work, he either found an algebraic method for computing maxima of polynomials, or he began the field of infinitesimal calculus. For example, Mahoney's position is that Fermat's methods were essentially algebraic and not an introduction to limits or infinitesimals. On the other hand Katz & Katz wrote that Fermat provided the seeds of the solution to the infinitesimal puzzle a century before George BerkeleyGeorge Berkeley
George Berkeley , also known as Bishop Berkeley , was an Irish philosopher whose primary achievement was the advancement of a theory he called "immaterialism"...
ever lifted up his pen to write The Analyst
The Analyst
The Analyst, subtitled "A DISCOURSE Addressed to an Infidel MATHEMATICIAN. WHEREIN It is examined whether the Object, Principles, and Inferences of the modern Analysis are more distinctly conceived, or more evidently deduced, than Religious Mysteries and Points of Faith", is a book published by...
.
Regardless of whether or not his work is viewed today as infinitesimal calculus his method yielded results that were far from trivial. Grabiner writes that he used his principle to give a mathematical derivation of Snell's laws of refraction directly from the principle that light takes the quickest path.

