Infinitesimal calculus
Encyclopedia
Infinitesimal calculus is the part of mathematics
concerned with finding slope of curve
s, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz
and Isaac Newton
starting in the 1660s. John Wallis exploited an infinitesimal he denoted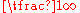
in area calculations, preparing the ground for integral calculus. They drew on the work of such mathematicians as Barrow
and Descartes
. It consisted of differential calculus
and integral calculus, respectively used for the techniques of differentiation and integration.
Newton sought to remove the use of infinitesimals from his fluxional calculus, preferring to talk of velocities as in "For by the ultimate velocity is meant ... the ultimate ratio of evanescent quantities". Leibniz embraced the concept fully calling differentials "...an evanescent quantity which yet retains the character of that which is disappearing", and his notation for them is the current symbolism in calculus, though Newton's occasionally appears in physics and other fields.
In early calculus the use of infinitesimal
quantities was unrigorous, and was fiercely criticized by a number of authors, most notably Michel Rolle
and Bishop Berkeley
. Berkeley famously described infinitesimals in his book The Analyst
in 1734.
Several mathematicians, including Maclaurin
and d'Alembert
, attempted to prove the soundness of using limits, but it would be 150 years later, due to the work of Cauchy
and Weierstrass
, where a means was finally found to avoid mere "notions" of infinitely small quantities, that the foundations of differential and integral calculus were made firm. In Cauchy's writing, we find a versatile spectrum of foundational approaches, including a definition of continuity
in terms of infinitesimals, and a (somewhat imprecise) prototype of an (ε, δ)-definition of limit in the definition of differentiation. In his work Weierstrass formalized the concept of limit
and eliminated infinitesimals. Following the work of Weierstrass, it eventually became common to base calculus on limits instead of infinitesimal quantities.
This approach formalized by Weierstrass came to be known as the standard calculus
. Informally, the name "infinitesimal calculus" became commonly used to refer to Weierstrass' approach.
in the 1960s. Robinson's approach, called non-standard analysis
, uses technical machinery from mathematical logic
to create a theory of hyperreal number
s that interpret infinitesimals in a manner that allows a Leibniz-like development of the usual rules of calculus.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
concerned with finding slope of curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
and Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
starting in the 1660s. John Wallis exploited an infinitesimal he denoted
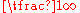in area calculations, preparing the ground for integral calculus. They drew on the work of such mathematicians as BarrowIsaac Barrow
Isaac Barrow was an English Christian theologian, and mathematician who is generally given credit for his early role in the development of infinitesimal calculus; in particular, for the discovery of the fundamental theorem of calculus. His work centered on the properties of the tangent; Barrow was...
and Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
. It consisted of differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
and integral calculus, respectively used for the techniques of differentiation and integration.
Newton sought to remove the use of infinitesimals from his fluxional calculus, preferring to talk of velocities as in "For by the ultimate velocity is meant ... the ultimate ratio of evanescent quantities". Leibniz embraced the concept fully calling differentials "...an evanescent quantity which yet retains the character of that which is disappearing", and his notation for them is the current symbolism in calculus, though Newton's occasionally appears in physics and other fields.
In early calculus the use of infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
quantities was unrigorous, and was fiercely criticized by a number of authors, most notably Michel Rolle
Michel Rolle
Michel Rolle was a French mathematician. He is best known for Rolle's theorem , and he deserves to be known as the co-inventor in Europe of Gaussian elimination .-Life:...
and Bishop Berkeley
George Berkeley
George Berkeley , also known as Bishop Berkeley , was an Irish philosopher whose primary achievement was the advancement of a theory he called "immaterialism"...
. Berkeley famously described infinitesimals in his book The Analyst
The Analyst
The Analyst, subtitled "A DISCOURSE Addressed to an Infidel MATHEMATICIAN. WHEREIN It is examined whether the Object, Principles, and Inferences of the modern Analysis are more distinctly conceived, or more evidently deduced, than Religious Mysteries and Points of Faith", is a book published by...
in 1734.
Several mathematicians, including Maclaurin
Colin Maclaurin
Colin Maclaurin was a Scottish mathematician who made important contributions to geometry and algebra. The Maclaurin series, a special case of the Taylor series, are named after him....
and d'Alembert
Jean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
, attempted to prove the soundness of using limits, but it would be 150 years later, due to the work of Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
and Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
, where a means was finally found to avoid mere "notions" of infinitely small quantities, that the foundations of differential and integral calculus were made firm. In Cauchy's writing, we find a versatile spectrum of foundational approaches, including a definition of continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
in terms of infinitesimals, and a (somewhat imprecise) prototype of an (ε, δ)-definition of limit in the definition of differentiation. In his work Weierstrass formalized the concept of limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
and eliminated infinitesimals. Following the work of Weierstrass, it eventually became common to base calculus on limits instead of infinitesimal quantities.
This approach formalized by Weierstrass came to be known as the standard calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. Informally, the name "infinitesimal calculus" became commonly used to refer to Weierstrass' approach.
Modern infinitesimals
After many years of the infinitesimal approach to calculus having fallen into disuse other than as an introductory pedagogical tool, use of infinitesimal quantities was finally given a rigorous foundation by Abraham RobinsonAbraham Robinson
Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
in the 1960s. Robinson's approach, called non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
, uses technical machinery from mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
to create a theory of hyperreal number
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
s that interpret infinitesimals in a manner that allows a Leibniz-like development of the usual rules of calculus.
Varieties of infinitesimal calculus
- DifferentialDifferential calculusIn mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
and integral calculus: together, the original infinitesimal calculus, due to Newton and Leibniz. - Standard calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
(based on the approach of Weierstrass) - Non-standard calculusNon-standard calculusIn mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus...
(based on Robinson's approach to infinitesimals)