John Wallis
Encyclopedia
John Wallis was an English mathematician
who is given partial credit for the development of infinitesimal calculus
. Between 1643 and 1689 he served as chief cryptographer for Parliament
and, later, the royal court. He is also credited with introducing the symbol
for infinity
. He similarly used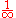
for an infinitesimal
. Asteroid
31982 Johnwallis
was named after him.
, the third of five children of Reverend John Wallis and Joanna Chapman. He was initially educated at a local Ashford school, but moved to James Movat's school in Tenterden
in 1625 following an outbreak of plague
. Wallis was first exposed to mathematics in 1631, at Martin Holbeach's school in Felsted
; he enjoyed maths, but his study was erratic, since: "mathematics, at that time with us, were scarce looked on as academical studies, but rather mechanical" (Scriba 1970).
As it was intended that he should be a doctor, he was sent in 1632 to Emmanuel College, Cambridge
. While there, he kept an act on the doctrine of the circulation of the blood; that was said to have been the first occasion in Europe on which this theory was publicly maintained in a disputation. His interests, however, centred on mathematics. He received his Bachelor of Arts degree in 1637, and a Master's in 1640, afterwards entering the priesthood. From 1643–49, he served as a non-voting scribe at the Westminster Assembly
. Wallis was elected to a fellowship at Queens' College, Cambridge
in 1644, which he however had to resign following his marriage.
Throughout this time, Wallis had been close to the Parliamentarian party, perhaps as a result of his exposure to Holbeach at Felsted School. He rendered them great practical assistance in deciphering Royalist dispatches. The quality of cryptography at that time was mixed; despite the individual successes of mathematicians such as François Viète
, the principles underlying cipher design and analysis were very poorly understood. Most ciphers were ad-hoc methods relying on a secret algorithm
, as opposed to systems based on a variable key
. Wallis realised that the latter were far more secure – even describing them as "unbreakable", though he was not confident enough in this assertion to encourage revealing cryptographic algorithms. He was also concerned about the use of ciphers by foreign powers; refusing, for example, Gottfried Leibniz
's request of 1697 to teach Hanoverian
students about cryptography.
Returning to London – he had been made chaplain at St Gabriel Fenchurch
, in 1643 – Wallis joined the group of scientists that was later to evolve into the Royal Society
. He was finally able to indulge his mathematical interests, mastering William Oughtred
's Clavis Mathematicae in a few weeks in 1647. He soon began to write his own treatises, dealing with a wide range of topics, continuing throughout his life.
Wallis joined the moderate Presbyterians in signing the remonstrance against the execution of Charles I
, by which he incurred the lasting hostility of the Independents. In spite of their opposition he was appointed in 1649 to be the Savilian Chair of Geometry
at Oxford University, where he lived until his death on 28 October 1703. In 1661, he was one of twelve Presbyterian representatives at the Savoy Conference
.
Besides his mathematical works he wrote on theology
, logic
, English grammar
and philosophy, and he was involved in devising a system for teaching deaf-mutes. Although William Holder
had earlier taught a deaf man Alexander Popham
to speak ‘plainly and distinctly, and with a good and graceful tone’. Wallis later claimed credit for this, leading Holder to accuse Wallis of 'rifling his Neighbours, and adorning himself with their spoyls’.
, calculus
, geometry
, and the analysis of infinite series. In his Opera Mathematica I (1695) Wallis introduced the term "continued fraction
".
Wallis rejected as absurd the now usual idea of a negative number as being less than nothing, but accepted the view that it is something greater than infinity. (The argument that negative numbers are greater than infinity involves the quotient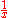
and considering what happens as x approaches and then crosses the point x = 0 from the positive side.) Despite this he is generally credited as the originator of the idea of the number line
where numbers are represented geometrically in a line with the positive numbers increasing to the right and negative numbers to the left.
' work on analytic geometry
.
It was in the Treatise on the Conic Sections that John Wallis popularised the symbol ∞ for infinity. He wrote, “I suppose any plane (following the Geometry of Indivisibles of Cavalieri) to be made up of an infinite number of parallel lines, or as I would prefer, of an infinite number of parallelograms of the same altitude; (let the altitude of each one of these be an infinitely small part,
of the whole altitude, and let the symbol ∞ denote Infinity) and the altitude of all to make up the altitude of the figure.”
were systematised and extended, but some ideals were open to criticism. He begins, after a short tract on conic sections, by developing the standard notation for powers, extending them from positive integers to rational numbers:
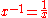
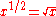
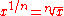
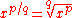
Leaving the numerous algebraic applications of this discovery, he next proceeds to find, by integration
, the area enclosed between the curve y = xm, the axis of x, and any ordinate x = h, and he proves that the ratio of this area to that of the parallelogram on the same base and of the same height is 1/(m + 1), extending Cavalieri's quadrature formula. He apparently assumed that the same result would be true also for the curve y = axm, where a is any constant, and m any number positive or negative; but he discusses only the case of the parabola in which m = 2, and that of the hyperbola in which m = −1. In the latter case, his interpretation of the result is incorrect. He then shows that similar results may be written down for any curve of the form
and hence that, if the ordinate y of a curve can be expanded in powers of x, its area can be determined: thus he says that if the equation of the curve is y = x0 + x1 + x2 + ..., its area would be x + x2/2 + x3/3 + ... He then applies this to the quadrature
of the curves y = (x − x2)0, y = (x − x2)1, y = (x − x2)2, etc., taken between the limits x = 0 and x = 1. He shows that the areas are respectively 1, 1/6, 1/30, 1/140, etc. He next considers curves of the form y = x1/m and establishes the theorem that the area bounded by this curve and the lines x = 0 and x = 1 is equal to the area of the rectangle on the same base and of the same altitude as m : m + 1. This is equivalent to computing
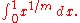
He illustrates this by the parabola, in which case m = 2. He states, but does not prove, the corresponding result for a curve of the form y = xp/q.
Wallis showed considerable ingenuity in reducing the equations of curves to the forms given above, but, as he was unacquainted with the binomial theorem
, he could not effect the quadrature of the circle, whose equation is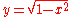
, since he was unable to expand this in powers of x. He laid down, however, the principle of interpolation
. Thus, as the ordinate of the circle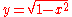
is the geometrical mean
between the ordinates of the curves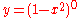
and 
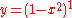, it might be supposed that, as an approximation, the area of the semicircle 
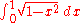which is 
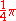might be taken as the geometrical mean between the values of
that is, 1 and
; this is equivalent to taking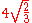 
or 3.26... as the value of π. But, Wallis argued, we have in fact a series 
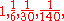... and therefore the term interpolated between 1 and 
ought to be chosen so as to obey the law of this series. This, by an elaborate method that is not described here in detail, leads to a value for the interpolated term which is equivalent to taking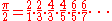
(which is now known as the Wallis product).
In this work also the formation and properties of continued fraction
s are discussed, the subject having been brought into prominence by Brouncker's use of these fractions.
A few years later, in 1659, Wallis published a tract containing the solution of the problems on the cycloid
which had been proposed by Blaise Pascal
. In this he incidentally explained how the principles laid down in his Arithmetica Infinitorum could be used for the rectification of algebraic curves; and gave a solution of the problem to rectify (i.e. find the length of) the semi-cubical parabola x3 = ay2, which had been discovered in 1657 by his pupil William Neile
. Since all attempts to rectify the ellipse and hyperbola had been (necessarily) ineffectual, it had been supposed that no curves could be rectified, as indeed Descartes had definitely asserted to be the case. The logarithmic spiral
had been rectified by Evangelista Torricelli
, and was the first curved line (other than the circle) whose length was determined, but the extension by Neil and Wallis to an algebraic curve was novel. The cycloid was the next curve rectified; this was done by Wren
in 1658.
Early in 1658 a similar discovery, independent of that of Neil, was made by van Heuraët, and this was published by van Schooten in his edition of Descartes's Geometria in 1659. Van Heuraët's method is as follows. He supposes the curve to be referred to rectangular axes; if this be so, and if (x, y) be the coordinates of any point on it, and n be the length of the normal, and if another point whose coordinates are (x, η) be taken such that η : h = n : y, where h is a constant; then, if ds be the element of the length of the required curve, we have by similar triangles ds : dx = n : y. Therefore h ds = η dx. Hence, if the area of the locus of the point (x, η) can be found, the first curve can be rectified. In this way van Heuraët effected the rectification of the curve y3 = ax2 but added that the rectification of the parabola y2 = ax is impossible since it requires the quadrature of the hyperbola. The solutions given by Neile and Wallis are somewhat similar to that given by van Heuraët, though no general rule is enunciated, and the analysis is clumsy. A third method was suggested by Fermat
in 1660, but it is inelegant and laborious.
in 1668 for the consideration of mathematicians. Wallis, Christopher Wren
, and Christian Huygens sent correct and similar solutions, all depending on what is now called the conservation of momentum; but, while Wren and Huygens confined their theory to perfectly elastic bodies (elastic collision
), Wallis considered also imperfectly elastic bodies (inelastic collision
). This was followed in 1669 by a work on statics
(centres of gravity), and in 1670 by one on dynamics
: these provide a convenient synopsis of what was then known on the subject
where s is the number representing the ratio of the space described to the unit of length; while the previous writers would have denoted the same relation by stating what is equivalent to the proposition
using similar triangles. However, Thabit Ibn Qurra
(AD 901), an Arab mathematician, had produced a generalisation of the Pythagorean theorem applicable to all triangles six centuries earlier. It is a reasonable conjecture that Wallis was aware of Thabit's work.
Wallis was also inspired by the works of Islamic mathematician Sadr al-Tusi, the son of Nasir al-Din al-Tusi
, particularly by al-Tusi's book written in 1298 on the parallel postulate
. The book was based on his father's thoughts which presented one of the earliest arguments for a non-Euclidean hypothesis equivalent to the parallel postulate. After reading this, Wallis then wrote about his ideas as he developed his own thoughts about the postulate, trying to prove it also with similar triangles.
He found that Euclid's fifth postulate
is equivalent to the one currently named "Wallis postulate" after him. This postulate states that "There is no upper limit for the area of a triangle". This result was encompassed in a trend trying to deduce Euclid's fifth from the other four postulates which today is known to be impossible. It is quite remarkable that, unlike other authors, he realised that the unbounded growth for the area of a triangle was not guaranteed by the four first postulates.
, the Secretary of the Royal Society, sent a colleague to investigate how Wallis did it. It was considered important enough to merit discussion in the Philosophical Transactions of the Royal Society of 1685.
arose in the mid-1650s, when mathematicians criticised errors in the work De corpore
by Hobbes. It continued into the 1670s, having gathered in the later claims of Hobbes on squaring the circle
, and the wider beliefs on both sides.
, Bryennius, and Porphyrius's commentary on Ptolemy. He also published three letters to Henry Oldenburg
concerning tuning. He approved of equal temperament that was being used in England's organs.
, that remained in print well into the eighteenth century. He also published on theology.
by Iain Pears
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
who is given partial credit for the development of infinitesimal calculus
Infinitesimal calculus
Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
. Between 1643 and 1689 he served as chief cryptographer for Parliament
Parliament of the United Kingdom
The Parliament of the United Kingdom of Great Britain and Northern Ireland is the supreme legislative body in the United Kingdom, British Crown dependencies and British overseas territories, located in London...
and, later, the royal court. He is also credited with introducing the symbol
Symbol
A symbol is something which represents an idea, a physical entity or a process but is distinct from it. The purpose of a symbol is to communicate meaning. For example, a red octagon may be a symbol for "STOP". On a map, a picture of a tent might represent a campsite. Numerals are symbols for...
for infinityInfinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
. He similarly used
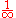for an infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
. Asteroid
Asteroid
Asteroids are a class of small Solar System bodies in orbit around the Sun. They have also been called planetoids, especially the larger ones...
31982 Johnwallis
31982 Johnwallis
31982 Johnwallis is a main-belt asteroid discovered on April 30, 2000 by P. G. Comba at Prescott.- External links :*...
was named after him.
Life
John Brehaut Wallis was born in Ashford, KentAshford, Kent
Ashford is a town in the borough of Ashford in Kent, England. In 2005 it was voted the fourth best place to live in the United Kingdom. It lies on the Great Stour river, the M20 motorway, and the South Eastern Main Line and High Speed 1 railways. Its agricultural market is one of the most...
, the third of five children of Reverend John Wallis and Joanna Chapman. He was initially educated at a local Ashford school, but moved to James Movat's school in Tenterden
Tenterden
Tenterden is a Cinque Port town in the Ashford District of Kent, England. It stands on the edge of the Weald, overlooking the valley of the River Rother....
in 1625 following an outbreak of plague
Bubonic plague
Plague is a deadly infectious disease that is caused by the enterobacteria Yersinia pestis, named after the French-Swiss bacteriologist Alexandre Yersin. Primarily carried by rodents and spread to humans via fleas, the disease is notorious throughout history, due to the unrivaled scale of death...
. Wallis was first exposed to mathematics in 1631, at Martin Holbeach's school in Felsted
Felsted School
Felsted School, an English co-educational day and boarding independent school, situated in Felsted, Essex. It is in the British Public School tradition, and was founded in 1564 by Richard Rich, 1st Baron Rich who, as Lord Chancellor and Chancellor of the Court of Augmentations, acquired...
; he enjoyed maths, but his study was erratic, since: "mathematics, at that time with us, were scarce looked on as academical studies, but rather mechanical" (Scriba 1970).
As it was intended that he should be a doctor, he was sent in 1632 to Emmanuel College, Cambridge
Emmanuel College, Cambridge
Emmanuel College is a constituent college of the University of Cambridge.The college was founded in 1584 by Sir Walter Mildmay on the site of a Dominican friary...
. While there, he kept an act on the doctrine of the circulation of the blood; that was said to have been the first occasion in Europe on which this theory was publicly maintained in a disputation. His interests, however, centred on mathematics. He received his Bachelor of Arts degree in 1637, and a Master's in 1640, afterwards entering the priesthood. From 1643–49, he served as a non-voting scribe at the Westminster Assembly
Westminster Assembly
The Westminster Assembly of Divines was appointed by the Long Parliament to restructure the Church of England. It also included representatives of religious leaders from Scotland...
. Wallis was elected to a fellowship at Queens' College, Cambridge
Queens' College, Cambridge
Queens' College is a constituent college of the University of Cambridge, England.The college was founded in 1448 by Margaret of Anjou , and refounded in 1465 by Elizabeth Woodville...
in 1644, which he however had to resign following his marriage.
Throughout this time, Wallis had been close to the Parliamentarian party, perhaps as a result of his exposure to Holbeach at Felsted School. He rendered them great practical assistance in deciphering Royalist dispatches. The quality of cryptography at that time was mixed; despite the individual successes of mathematicians such as François Viète
François Viète
François Viète , Seigneur de la Bigotière, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to its innovative use of letters as parameters in equations...
, the principles underlying cipher design and analysis were very poorly understood. Most ciphers were ad-hoc methods relying on a secret algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, as opposed to systems based on a variable key
Key (cryptography)
In cryptography, a key is a piece of information that determines the functional output of a cryptographic algorithm or cipher. Without a key, the algorithm would produce no useful result. In encryption, a key specifies the particular transformation of plaintext into ciphertext, or vice versa...
. Wallis realised that the latter were far more secure – even describing them as "unbreakable", though he was not confident enough in this assertion to encourage revealing cryptographic algorithms. He was also concerned about the use of ciphers by foreign powers; refusing, for example, Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
's request of 1697 to teach Hanoverian
Electorate of Hanover
The Electorate of Brunswick-Lüneburg was the ninth Electorate of the Holy Roman Empire of the German Nation...
students about cryptography.
Returning to London – he had been made chaplain at St Gabriel Fenchurch
St Gabriel Fenchurch
St Gabriel Fenchurch was a parish church in the Langbourn Ward of the City of London, destroyed in the Great Fire of London and not rebuilt.-History:The church stood between Rood Lane and Mincing Lane...
, in 1643 – Wallis joined the group of scientists that was later to evolve into the Royal Society
Royal Society
The Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...
. He was finally able to indulge his mathematical interests, mastering William Oughtred
William Oughtred
William Oughtred was an English mathematician.After John Napier invented logarithms, and Edmund Gunter created the logarithmic scales upon which slide rules are based, it was Oughtred who first used two such scales sliding by one another to perform direct multiplication and division; and he is...
's Clavis Mathematicae in a few weeks in 1647. He soon began to write his own treatises, dealing with a wide range of topics, continuing throughout his life.
Wallis joined the moderate Presbyterians in signing the remonstrance against the execution of Charles I
Charles I of England
Charles I was King of England, King of Scotland, and King of Ireland from 27 March 1625 until his execution in 1649. Charles engaged in a struggle for power with the Parliament of England, attempting to obtain royal revenue whilst Parliament sought to curb his Royal prerogative which Charles...
, by which he incurred the lasting hostility of the Independents. In spite of their opposition he was appointed in 1649 to be the Savilian Chair of Geometry
Savilian Professor of Geometry
The position of Savilian Professor of Geometry was established at the University of Oxford in 1619. It was founded by Sir Henry Savile, a mathematician and classical scholar who was Warden of Merton College, Oxford and Provost of Eton College, reacting to what has been described as "the wretched...
at Oxford University, where he lived until his death on 28 October 1703. In 1661, he was one of twelve Presbyterian representatives at the Savoy Conference
Savoy Conference
The Savoy Conference of 1661 was a significant liturgical discussion that took place, after the Restoration of Charles II, in an attempt to effect a reconciliation within the Church of England.-Proceedings:...
.
Besides his mathematical works he wrote on theology
Theology
Theology is the systematic and rational study of religion and its influences and of the nature of religious truths, or the learned profession acquired by completing specialized training in religious studies, usually at a university or school of divinity or seminary.-Definition:Augustine of Hippo...
, logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, English grammar
English grammar
English grammar is the body of rules that describe the structure of expressions in the English language. This includes the structure of words, phrases, clauses and sentences...
and philosophy, and he was involved in devising a system for teaching deaf-mutes. Although William Holder
William Holder
William Holder FRS was an English clergyman and music theorist of the 17th century. His most notable work was his widely known 1694 publication A Treatise on the Natural Grounds and Principles of Harmony.-Life:...
had earlier taught a deaf man Alexander Popham
Alexander Popham
Alexander Popham, of Littlecote, Wiltshire was an English politician. He is now remembered for his role as patron of the philosopher John Locke....
to speak ‘plainly and distinctly, and with a good and graceful tone’. Wallis later claimed credit for this, leading Holder to accuse Wallis of 'rifling his Neighbours, and adorning himself with their spoyls’.
Contributions to mathematics
Wallis made significant contributions to trigonometryTrigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, and the analysis of infinite series. In his Opera Mathematica I (1695) Wallis introduced the term "continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
".
Wallis rejected as absurd the now usual idea of a negative number as being less than nothing, but accepted the view that it is something greater than infinity. (The argument that negative numbers are greater than infinity involves the quotient
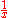and considering what happens as x approaches and then crosses the point x = 0 from the positive side.) Despite this he is generally credited as the originator of the idea of the number lineNumber line
In basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point. Often the integers are shown as specially-marked points evenly spaced on the line...
where numbers are represented geometrically in a line with the positive numbers increasing to the right and negative numbers to the left.
Analytical geometry
In 1655, Wallis published a treatise on conic sections in which they were defined analytically. This was the earliest book in which these curves are considered and defined as curves of the second degree. It helped to remove some of the perceived difficulty and obscurity of René DescartesRené Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
' work on analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
.
It was in the Treatise on the Conic Sections that John Wallis popularised the symbol ∞ for infinity. He wrote, “I suppose any plane (following the Geometry of Indivisibles of Cavalieri) to be made up of an infinite number of parallel lines, or as I would prefer, of an infinite number of parallelograms of the same altitude; (let the altitude of each one of these be an infinitely small part,
of the whole altitude, and let the symbol ∞ denote Infinity) and the altitude of all to make up the altitude of the figure.”Integral calculus
Arithmetica Infinitorum, the most important of Wallis's works, was published in 1656. In this treatise the methods of analysis of Descartes and CavalieriBonaventura Cavalieri
Bonaventura Francesco Cavalieri was an Italian mathematician. He is known for his work on the problems of optics and motion, work on the precursors of infinitesimal calculus, and the introduction of logarithms to Italy...
were systematised and extended, but some ideals were open to criticism. He begins, after a short tract on conic sections, by developing the standard notation for powers, extending them from positive integers to rational numbers:
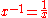
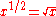
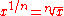
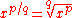
Leaving the numerous algebraic applications of this discovery, he next proceeds to find, by integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, the area enclosed between the curve y = xm, the axis of x, and any ordinate x = h, and he proves that the ratio of this area to that of the parallelogram on the same base and of the same height is 1/(m + 1), extending Cavalieri's quadrature formula. He apparently assumed that the same result would be true also for the curve y = axm, where a is any constant, and m any number positive or negative; but he discusses only the case of the parabola in which m = 2, and that of the hyperbola in which m = −1. In the latter case, his interpretation of the result is incorrect. He then shows that similar results may be written down for any curve of the form
and hence that, if the ordinate y of a curve can be expanded in powers of x, its area can be determined: thus he says that if the equation of the curve is y = x0 + x1 + x2 + ..., its area would be x + x2/2 + x3/3 + ... He then applies this to the quadrature
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
of the curves y = (x − x2)0, y = (x − x2)1, y = (x − x2)2, etc., taken between the limits x = 0 and x = 1. He shows that the areas are respectively 1, 1/6, 1/30, 1/140, etc. He next considers curves of the form y = x1/m and establishes the theorem that the area bounded by this curve and the lines x = 0 and x = 1 is equal to the area of the rectangle on the same base and of the same altitude as m : m + 1. This is equivalent to computing
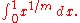
He illustrates this by the parabola, in which case m = 2. He states, but does not prove, the corresponding result for a curve of the form y = xp/q.
Wallis showed considerable ingenuity in reducing the equations of curves to the forms given above, but, as he was unacquainted with the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
, he could not effect the quadrature of the circle, whose equation is
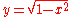, since he was unable to expand this in powers of x. He laid down, however, the principle of interpolationInterpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
. Thus, as the ordinate of the circle
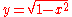is the geometrical meanGeometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
between the ordinates of the curves
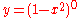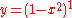and , it might be supposed that, as an approximation, the area of the semicircle 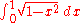which is 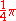might be taken as the geometrical mean between the values ofthat is, 1 and
; this is equivalent to taking 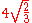or 3.26... as the value of π. But, Wallis argued, we have in fact a series 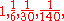... and therefore the term interpolated between 1 and ought to be chosen so as to obey the law of this series. This, by an elaborate method that is not described here in detail, leads to a value for the interpolated term which is equivalent to taking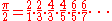(which is now known as the Wallis product).
In this work also the formation and properties of continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s are discussed, the subject having been brought into prominence by Brouncker's use of these fractions.
A few years later, in 1659, Wallis published a tract containing the solution of the problems on the cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
which had been proposed by Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
. In this he incidentally explained how the principles laid down in his Arithmetica Infinitorum could be used for the rectification of algebraic curves; and gave a solution of the problem to rectify (i.e. find the length of) the semi-cubical parabola x3 = ay2, which had been discovered in 1657 by his pupil William Neile
William Neile
William Neile was an English mathematician and founder member of the Royal Society. His major mathematical work, the rectification of the semicubical parabola, was carried out when he was aged nineteen, and was published by John Wallis...
. Since all attempts to rectify the ellipse and hyperbola had been (necessarily) ineffectual, it had been supposed that no curves could be rectified, as indeed Descartes had definitely asserted to be the case. The logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
had been rectified by Evangelista Torricelli
Evangelista Torricelli
Evangelista Torricelli was an Italian physicist and mathematician, best known for his invention of the barometer.-Biography:Evangelista Torricelli was born in Faenza, part of the Papal States...
, and was the first curved line (other than the circle) whose length was determined, but the extension by Neil and Wallis to an algebraic curve was novel. The cycloid was the next curve rectified; this was done by Wren
Christopher Wren
Sir Christopher Wren FRS is one of the most highly acclaimed English architects in history.He used to be accorded responsibility for rebuilding 51 churches in the City of London after the Great Fire in 1666, including his masterpiece, St. Paul's Cathedral, on Ludgate Hill, completed in 1710...
in 1658.
Early in 1658 a similar discovery, independent of that of Neil, was made by van Heuraët, and this was published by van Schooten in his edition of Descartes's Geometria in 1659. Van Heuraët's method is as follows. He supposes the curve to be referred to rectangular axes; if this be so, and if (x, y) be the coordinates of any point on it, and n be the length of the normal, and if another point whose coordinates are (x, η) be taken such that η : h = n : y, where h is a constant; then, if ds be the element of the length of the required curve, we have by similar triangles ds : dx = n : y. Therefore h ds = η dx. Hence, if the area of the locus of the point (x, η) can be found, the first curve can be rectified. In this way van Heuraët effected the rectification of the curve y3 = ax2 but added that the rectification of the parabola y2 = ax is impossible since it requires the quadrature of the hyperbola. The solutions given by Neile and Wallis are somewhat similar to that given by van Heuraët, though no general rule is enunciated, and the analysis is clumsy. A third method was suggested by Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
in 1660, but it is inelegant and laborious.
Collision of bodies
The theory of the collision of bodies was propounded by the Royal SocietyRoyal Society
The Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...
in 1668 for the consideration of mathematicians. Wallis, Christopher Wren
Christopher Wren
Sir Christopher Wren FRS is one of the most highly acclaimed English architects in history.He used to be accorded responsibility for rebuilding 51 churches in the City of London after the Great Fire in 1666, including his masterpiece, St. Paul's Cathedral, on Ludgate Hill, completed in 1710...
, and Christian Huygens sent correct and similar solutions, all depending on what is now called the conservation of momentum; but, while Wren and Huygens confined their theory to perfectly elastic bodies (elastic collision
Elastic collision
An elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter...
), Wallis considered also imperfectly elastic bodies (inelastic collision
Inelastic collision
An inelastic collision, in contrast to an elastic collision, is a collision in which kinetic energy is not conserved.In collisions of macroscopic bodies, some kinetic energy is turned into vibrational energy of the atoms, causing a heating effect, and the bodies are deformed.The molecules of a gas...
). This was followed in 1669 by a work on statics
Statics
Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
(centres of gravity), and in 1670 by one on dynamics
Analytical dynamics
In classical mechanics, analytical dynamics, or more briefly dynamics, is concerned about the relationship between motion of bodies and its causes, namely the forces acting on the bodies and the properties of the bodies...
: these provide a convenient synopsis of what was then known on the subject
Algebra
In 1685 Wallis published Algebra, preceded by a historical account of the development of the subject, which contains a great deal of valuable information. The second edition, issued in 1693 and forming the second volume of his Opera, was considerably enlarged. This algebra is noteworthy as containing the first systematic use of formulae. A given magnitude is here represented by the numerical ratio which it bears to the unit of the same kind of magnitude: thus, when Wallis wants to compare two lengths he regards each as containing so many units of length. This perhaps will be made clearer by noting that the relation between the space described in any time by a particle moving with a uniform velocity is denoted by Wallis by the formula- s = vt,
where s is the number representing the ratio of the space described to the unit of length; while the previous writers would have denoted the same relation by stating what is equivalent to the proposition
- s1 : s2 = v1t1 : v2t2.
Geometry
He is usually credited with the proof of the Pythagorean theoremPythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
using similar triangles. However, Thabit Ibn Qurra
Thabit ibn Qurra
' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
(AD 901), an Arab mathematician, had produced a generalisation of the Pythagorean theorem applicable to all triangles six centuries earlier. It is a reasonable conjecture that Wallis was aware of Thabit's work.
Wallis was also inspired by the works of Islamic mathematician Sadr al-Tusi, the son of Nasir al-Din al-Tusi
Nasir al-Din al-Tusi
Khawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
, particularly by al-Tusi's book written in 1298 on the parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
. The book was based on his father's thoughts which presented one of the earliest arguments for a non-Euclidean hypothesis equivalent to the parallel postulate. After reading this, Wallis then wrote about his ideas as he developed his own thoughts about the postulate, trying to prove it also with similar triangles.
He found that Euclid's fifth postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
is equivalent to the one currently named "Wallis postulate" after him. This postulate states that "There is no upper limit for the area of a triangle". This result was encompassed in a trend trying to deduce Euclid's fifth from the other four postulates which today is known to be impossible. It is quite remarkable that, unlike other authors, he realised that the unbounded growth for the area of a triangle was not guaranteed by the four first postulates.
Calculator
One aspect of Wallis's mathematical skills has not yet been mentioned, namely his great ability to do mental calculations. He slept badly and often did mental calculations as he lay awake in his bed. One night he calculated in his head the square root of a number with 53 digits. In the morning he dictated the 27-digit square root of the number, still entirely from memory. It was a feat that was rightly considered remarkable, and Henry OldenburgHenry Oldenburg
Henry Oldenburg was a German theologian known as a diplomat and a natural philosopher. He was one of the foremost intelligencers of Europe of the seventeenth century, with a network of correspondents to rival those of Fabri de Peiresc, Marin Mersenne and Ismaël Boulliau...
, the Secretary of the Royal Society, sent a colleague to investigate how Wallis did it. It was considered important enough to merit discussion in the Philosophical Transactions of the Royal Society of 1685.
Controversy with Hobbes
A long-running debate between Wallis and Thomas HobbesThomas Hobbes
Thomas Hobbes of Malmesbury , in some older texts Thomas Hobbs of Malmsbury, was an English philosopher, best known today for his work on political philosophy...
arose in the mid-1650s, when mathematicians criticised errors in the work De corpore
De Corpore
De Corpore is a 1655 book by Thomas Hobbes. As its full Latin title Elementorum philosophiae sectio prima De corpore implies, it was part of a larger work, conceived as a trilogy. De Cive had already appeared, while De Homine would be published in 1658...
by Hobbes. It continued into the 1670s, having gathered in the later claims of Hobbes on squaring the circle
Squaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
, and the wider beliefs on both sides.
Music theory
Wallis translated into Latin works of PtolemyPtolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
, Bryennius, and Porphyrius's commentary on Ptolemy. He also published three letters to Henry Oldenburg
Henry Oldenburg
Henry Oldenburg was a German theologian known as a diplomat and a natural philosopher. He was one of the foremost intelligencers of Europe of the seventeenth century, with a network of correspondents to rival those of Fabri de Peiresc, Marin Mersenne and Ismaël Boulliau...
concerning tuning. He approved of equal temperament that was being used in England's organs.
Other works
His Institutio logicae, published in 1687, was very popular. The Grammatica linguae Anglicanae was a work on English grammarEnglish grammar
English grammar is the body of rules that describe the structure of expressions in the English language. This includes the structure of words, phrases, clauses and sentences...
, that remained in print well into the eighteenth century. He also published on theology.
Family
On 14 March 1645 he married Susanna Glyde (16??-16 March 1687) with three children:- John Wallis (26 December 1650-1???) married Elizabeth Harris (−1693) in 1 February 1682 with three children
- Anne Wallis (1656-1???), married Sir John Blencowe in 1675, with issue
- Elizabeth Wallis (1656–1700), married William Benson of Towcester with no issue
In fiction
Wallis is portrayed in an unfavourable way in the historical mystery novel An Instance of the FingerpostAn Instance of the Fingerpost
An Instance of the Fingerpost is a 1997 historical mystery novel by Iain Pears.-Synopsis:A murder in 17th-century Oxford is related from the contradictory points of view of four of the characters, all of them unreliable narrators...
by Iain Pears
Iain Pears
Iain Pears is an English art historian, novelist and journalist. He was educated at Warwick School, Warwick, Wadham College and Wolfson College, Oxford. Before writing, he worked as a reporter for the BBC, Channel 4 and ZDF and correspondent for Reuters from 1982 to 1990 in Italy, France, UK and...
.
See also
- Wallis’s conical edgeWallis’s conical edgeWallis's conical edge is a ruled surface given by the parametric equations:where a, b and c are constants.Wallis's conical edge is also a kind of right conoid.Figure 2 shows that the Wallis's conical edge is generated by a moving line....
- John Wallis Academy – former Christ Church school in Ashford renamed in 2010
- Invisible CollegeInvisible CollegeThe Invisible College has been described as a precursor group to the Royal Society of London, consisting of a number of natural philosophers around Robert Boyle...