Alexander's trick
Encyclopedia
Alexander's trick, also known as the Alexander trick, is a basic result in geometric topology
, named after J. W. Alexander
.
s of the n-dimension
al ball
which agree on the boundary
sphere
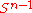are isotopic.
More generally, two homeomorphisms of Dn that are isotopic on the boundary are isotopic.
If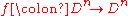
satisfies 
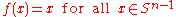, then an isotopy connecting f to the identity is given by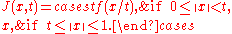
Visually, the homeomorphism is 'straightened out' from the boundary, 'squeezing'
down to the origin. William Thurston
calls this "combing all the tangles to one point".
The subtlety is that at
, 
"disappears": the germ
at the origin "jumps" from an infinitely stretched version of
to the identity. Each of the steps in the homotopy could be smoothed (smooth the transition), but the homotopy (the overall map) has a singularity at 
. This underlines that the Alexander trick is a PL construction, but not smooth.
General case: isotopic on boundary implies isotopic
If
are two homeomorphisms that agree on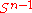 
, then 
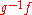is the identity on 
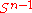, so we have an isotopy 
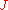from the identity to 
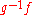. The map 
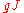is then an isotopy from 
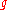to 
.
of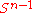
can be extended to a homeomorphism of the entire ball 
.
However, this is much easier to prove than the result discussed above: it is called radial extension (or coning) and is also true piecewise-linearly, but not smoothly.
Concretely, let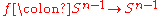
be a homeomorphism, then
defines a homeomorphism of the ball.
Exotic sphere
The failure of smooth radial extension and the success of PL radial extension
yield exotic sphere
s via twisted spheres.
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
, named after J. W. Alexander
James Waddell Alexander II
James Waddell Alexander II was a mathematician and topologist of the pre-World War II era and part of an influential Princeton topology elite, which included Oswald Veblen, Solomon Lefschetz, and others...
.
Statement
Two homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s of the n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
which agree on the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
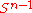are isotopic.More generally, two homeomorphisms of Dn that are isotopic on the boundary are isotopic.
Proof
Base case: every homeomorphism which fixes the boundary is isotopic to the identity relative to the boundary.If
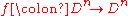satisfies 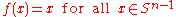, then an isotopy connecting f to the identity is given by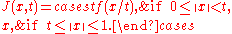Visually, the homeomorphism is 'straightened out' from the boundary, 'squeezing'
down to the origin. William ThurstonWilliam Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
calls this "combing all the tangles to one point".
The subtlety is that at
, "disappears": the germGerm (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
at the origin "jumps" from an infinitely stretched version of
to the identity. Each of the steps in the homotopy could be smoothed (smooth the transition), but the homotopy (the overall map) has a singularity at . This underlines that the Alexander trick is a PL construction, but not smooth.General case: isotopic on boundary implies isotopic
If
are two homeomorphisms that agree on 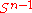, then 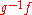is the identity on 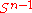, so we have an isotopy 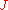from the identity to 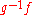. The map 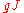is then an isotopy from 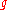to .Radial extension
Some authors use the term Alexander trick for the statement that every homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
of
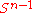can be extended to a homeomorphism of the entire ball .However, this is much easier to prove than the result discussed above: it is called radial extension (or coning) and is also true piecewise-linearly, but not smoothly.
Concretely, let
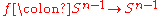be a homeomorphism, thendefines a homeomorphism of the ball.
Exotic sphereExotic sphereIn differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s
The failure of smooth radial extension and the success of PL radial extensionyield exotic sphere
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s via twisted spheres.