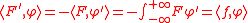In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 — specifically, in integration theory

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

 — the Alexiewicz norm is an integral norm

Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

 associated to the Henstock–Kurzweil integral. The Alexiewicz norm turns the space of Henstock–Kurzweil integrable functions into a topological vector space

Topological vector space

In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...

 that is barrelled

Barrelled space

In functional analysis and related areas of mathematics, barrelled spaces are Hausdorff topological vector spaces for which every barrelled set in the space is a neighbourhood for the zero vector. A barrelled set or a barrel in a topological vector space is a set which is convex, balanced,...

 but not complete

Complete space

In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....

. The Alexiewicz norm is named after the Polish

Poland

Poland , officially the Republic of Poland , is a country in Central Europe bordered by Germany to the west; the Czech Republic and Slovakia to the south; Ukraine, Belarus and Lithuania to the east; and the Baltic Sea and Kaliningrad Oblast, a Russian exclave, to the north...

 mathematician Andrzej Alexiewicz

Andrzej Alexiewicz

Andrzej Alexiewicz was a Polish mathematician, a disciple of the Lwow School of Mathematics. Alexiewicz was an expert at functional analysis and continued and edited the work of Stefan Banach....

, who introduced it in 1948.

Definition

Let HK(R) denote the space of all functions f: R → R that have finite Henstock–Kurzweil integral. Define the Alexiewicz semi-norm of f ∈ HK(R) by
This defines a semi-norm on HK(R); if functions that are equal Lebesgue

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

-almost everywhere

Almost everywhere

In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...

 are identified, then this procedure defines a bona fide norm on the quotient

Quotient space

In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...

 of HK(R) by the equivalence relation

Equivalence relation

In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...

 of equality almost everywhere. (Note that the only constant function f: R → R that is integrable is the one with constant value zero.)

Properties

• The Alexiewicz norm endows HK(R) with a topology that is barrelled but incomplete.
• The Alexiewicz norm as defined above is equivalent to the norm defined by

• The completion of HK(R) with respect to the Alexiewicz norm is often denoted A(R) and is a subspace of the space of tempered distribution
  Distribution (mathematics)
  In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
  
  s, the dual of Schwartz space. More precisely, A(R) consists of those tempered distributions that are distributional derivatives of functions in the collection

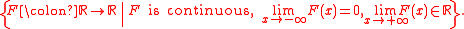
Therefore, if f ∈ A(R), then f is a tempered distribution and there exists a continuous function F in the above collection such that

for every compactly supported C^∞

Smooth function

In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...

 test function φ: R → R. In this case, it holds that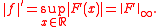

• The translation operator is continuous with respect to the Alexiewicz norm. That is, if for f ∈ HK(R) and x ∈ R the translation T_xf of f by x is defined by

then