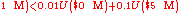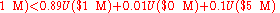Allais paradox
Encyclopedia
The Allais paradox is a choice problem designed by Maurice Allais
to show an inconsistency of actual observed choices with the predictions of expected utility theory.
Several studies involving hypothetical and small monetary payoffs, and recently involving health outcomes, have supported the assertion that when presented with a choice between 1A and 1B, most people would choose 1A. Likewise, when presented with a choice between 2A and 2B, most people would choose 2B. Allais further asserted that it was reasonable to choose 1A alone or 2B alone.
However, that the same person (who chose 1A alone or 2B alone) would choose both 1A and 2B together is inconsistent with expected utility theory. According to expected utility theory, the person should choose either 1A and 2A or 1B and 2B.
The inconsistency stems from the fact that in expected utility theory, equal outcomes added to each of the two choices should have no effect on the relative desirability of one gamble over the other; equal outcomes should "cancel out". Each experiment gives the same outcome 89% of the time (starting from the top row and moving down, both 1A and 1B give an outcome of $1 million, and both 2A and 2B give an outcome of nothing). If this 89% ‘common consequence’ is disregarded, then the gambles will be left offering the same choice.
It may help to re-write the payoffs. After disregarding the 89% chance of winning — the same outcome — then 1B is left offering a 1% chance of winning nothing and a 10% chance of winning $5 million, while 2B is also left offering a 1% chance of winning nothing and a 10% chance of winning $5 million. Hence, choice 1B and 2B can be seen as the same choice. In the same manner, 1A and 2A should also now be seen as the same choice.
Allais presented his paradox as a counterexample
to the independence axiom.
Independence means that if an agent is indifferent between simple lotteries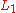
and 
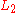, the agent is also indifferent between 
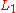mixed with an arbitrary simple lottery 
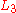with probability 
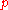and 
mixed with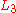 
with the same probability 
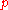. Violating this principle is known as the "common consequence" problem (or "common consequence" effect). The idea of the common consequence problem is that as the prize offered by 
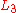increases, 
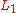and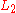 
become consolation prizes, and the agent will modify preferences between the two lotteries so as to minimize risk and disappointment in case they do not win the higher prize offered by 
.
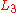Difficulties such as this gave rise to a number of alternatives to, and generalizations
of, the theory, notably including prospect theory
, developed by Daniel Kahneman
and Amos Tversky
, weighted utility (Chew), and rank-dependent expected utility
by John Quiggin
. The point of these models was to allow a wider range of behavior than was consistent with expected utility theory.
Also relevant here is the framing
theory of Daniel Kahneman
and Amos Tversky
. Identical items will result in different choices if presented to agents differently (i.e. a surgery with a 70% survival rate vs. a 30% chance of death).
The main point Allais wished to make is that the independence axiom of expected utility theory may not be a valid axiom. The independence axiom states that two identical outcomes within a gamble should be treated as irrelevant to the analysis of the gamble as a whole. However, this overlooks the notion of complementarities, the fact your choice in one part of a gamble may depend on the possible outcome in the other part of the gamble. In the above choice, 1B, there is a 1% chance of getting nothing. However, this 1% chance of getting nothing also carries with it a great sense of disappointment if you were to pick that gamble and lose, knowing you could have won with 100% certainty if you had chosen 1A. This feeling of disappointment, however, is contingent on the outcome in the other portion of the gamble (i.e. the feeling of certainty). Hence, Allais argues that it is not possible to evaluate portions of gambles or choices independently of the other choices presented, as the independence axiom requires, and thus is a poor judge of our rational action (1B cannot be valued independently of 1A as the independence or sure thing principle requires of us). We don't act irrationally when choosing 1A and 2B; rather expected utility theory is not robust enough to capture such "bounded rationality
" choices that in this case arise because of complementarities.
Because the typical individual prefers 1A to 1B and 2B to 2A, we can write conclude that the expected utilities of the preferred is greater than the expected utilities of the second choices, or,
We can rewrite the latter equation (Experiment 2) as
which contradicts the first bet (Experiment 1), which shows the player prefers the sure thing over the gamble.
Maurice Allais
Maurice Félix Charles Allais was a French economist, and was the 1988 winner of the Nobel Memorial Prize in Economics "for his pioneering contributions to the theory of markets and efficient utilization of resources."...
to show an inconsistency of actual observed choices with the predictions of expected utility theory.
Statement of the Problem
The Allais paradox arises when comparing participants' choices in two different experiments, each of which consists of a choice between two gambles, A and B. The payoffs for each gamble in each experiment are as follows:| Experiment 1 | Experiment 2 | ||||||
| Gamble 1A | Gamble 1B | Gamble 2A | Gamble 2B | ||||
| Winnings | Chance | Winnings | Chance | Winnings | Chance | Winnings | Chance |
| $1 million | 100% | $1 million | 89% | Nothing | 89% | Nothing | 90% |
| Nothing | 1% | $1 million | 11% | ||||
| $5 million | 10% | $5 million | 10% | ||||
Several studies involving hypothetical and small monetary payoffs, and recently involving health outcomes, have supported the assertion that when presented with a choice between 1A and 1B, most people would choose 1A. Likewise, when presented with a choice between 2A and 2B, most people would choose 2B. Allais further asserted that it was reasonable to choose 1A alone or 2B alone.
However, that the same person (who chose 1A alone or 2B alone) would choose both 1A and 2B together is inconsistent with expected utility theory. According to expected utility theory, the person should choose either 1A and 2A or 1B and 2B.
The inconsistency stems from the fact that in expected utility theory, equal outcomes added to each of the two choices should have no effect on the relative desirability of one gamble over the other; equal outcomes should "cancel out". Each experiment gives the same outcome 89% of the time (starting from the top row and moving down, both 1A and 1B give an outcome of $1 million, and both 2A and 2B give an outcome of nothing). If this 89% ‘common consequence’ is disregarded, then the gambles will be left offering the same choice.
It may help to re-write the payoffs. After disregarding the 89% chance of winning — the same outcome — then 1B is left offering a 1% chance of winning nothing and a 10% chance of winning $5 million, while 2B is also left offering a 1% chance of winning nothing and a 10% chance of winning $5 million. Hence, choice 1B and 2B can be seen as the same choice. In the same manner, 1A and 2A should also now be seen as the same choice.
| Experiment 1 | Experiment 2 | ||||||
| Gamble 1A | Gamble 1B | Gamble 2A | Gamble 2B | ||||
| Winnings | Chance | Winnings | Chance | Winnings | Chance | Winnings | Chance |
| $1 million | 89% | $1 million | 89% | Nothing | 89% | Nothing | 89% |
| $1 million | 11% | Nothing | 1% | $1 million | 11% | Nothing | 1% |
| $5 million | 10% | $5 million | 10% | ||||
Allais presented his paradox as a counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
to the independence axiom.
Independence means that if an agent is indifferent between simple lotteries
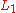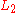and , the agent is also indifferent between 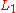mixed with an arbitrary simple lottery 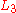with probability 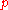and mixed with 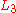with the same probability 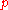. Violating this principle is known as the "common consequence" problem (or "common consequence" effect). The idea of the common consequence problem is that as the prize offered by 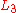increases, 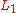and 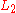become consolation prizes, and the agent will modify preferences between the two lotteries so as to minimize risk and disappointment in case they do not win the higher prize offered by 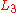.Difficulties such as this gave rise to a number of alternatives to, and generalizations
Generalized expected utility
The expected utility model developed by John von Neumann and Oskar Morgenstern dominated decision theory from its formulation in 1944 until the late 1970s, not only as a prescriptive, but also as a descriptive model, despite powerful criticism from Maurice Allais and Daniel Ellsberg who showed...
of, the theory, notably including prospect theory
Prospect theory
Prospect theory is a theory that describes decisions between alternatives that involve risk i.e. where the probabilities of outcomes are known. The model is descriptive: it tries to model real-life choices, rather than optimal decisions.-Model:...
, developed by Daniel Kahneman
Daniel Kahneman
Daniel Kahneman is an Israeli-American psychologist and Nobel laureate. He is notable for his work on the psychology of judgment and decision-making, behavioral economics and hedonic psychology....
and Amos Tversky
Amos Tversky
Amos Nathan Tversky, was a cognitive and mathematical psychologist, a pioneer of cognitive science, a longtime collaborator of Daniel Kahneman, and a key figure in the discovery of systematic human cognitive bias and handling of risk. Much of his early work concerned the foundations of measurement...
, weighted utility (Chew), and rank-dependent expected utility
Rank-dependent expected utility
The rank-dependent expected utility model is a generalized expected utility model of choice under uncertainty, designed to explain the behaviour observed in the Allais paradox, as well as for the observation that many people both purchase lottery tickets and insure against losses .A...
by John Quiggin
John Quiggin
John Quiggin is an Australian economist and professor at the University of Queensland. Quiggin studied at the Australian National University, obtaining bachelor's degrees in Arts and Economics in 1978 and 1980 respectively, and completing a master's degree in Economics in 1984. Quiggin was awarded...
. The point of these models was to allow a wider range of behavior than was consistent with expected utility theory.
Also relevant here is the framing
Framing (social sciences)
A frame in social theory consists of a schema of interpretation — that is, a collection of anecdotes and stereotypes—that individuals rely on to understand and respond to events. In simpler terms, people build a series of mental filters through biological and cultural influences. They use these...
theory of Daniel Kahneman
Daniel Kahneman
Daniel Kahneman is an Israeli-American psychologist and Nobel laureate. He is notable for his work on the psychology of judgment and decision-making, behavioral economics and hedonic psychology....
and Amos Tversky
Amos Tversky
Amos Nathan Tversky, was a cognitive and mathematical psychologist, a pioneer of cognitive science, a longtime collaborator of Daniel Kahneman, and a key figure in the discovery of systematic human cognitive bias and handling of risk. Much of his early work concerned the foundations of measurement...
. Identical items will result in different choices if presented to agents differently (i.e. a surgery with a 70% survival rate vs. a 30% chance of death).
The main point Allais wished to make is that the independence axiom of expected utility theory may not be a valid axiom. The independence axiom states that two identical outcomes within a gamble should be treated as irrelevant to the analysis of the gamble as a whole. However, this overlooks the notion of complementarities, the fact your choice in one part of a gamble may depend on the possible outcome in the other part of the gamble. In the above choice, 1B, there is a 1% chance of getting nothing. However, this 1% chance of getting nothing also carries with it a great sense of disappointment if you were to pick that gamble and lose, knowing you could have won with 100% certainty if you had chosen 1A. This feeling of disappointment, however, is contingent on the outcome in the other portion of the gamble (i.e. the feeling of certainty). Hence, Allais argues that it is not possible to evaluate portions of gambles or choices independently of the other choices presented, as the independence axiom requires, and thus is a poor judge of our rational action (1B cannot be valued independently of 1A as the independence or sure thing principle requires of us). We don't act irrationally when choosing 1A and 2B; rather expected utility theory is not robust enough to capture such "bounded rationality
Bounded rationality
Bounded rationality is the idea that in decision making, rationality of individuals is limited by the information they have, the cognitive limitations of their minds, and the finite amount of time they have to make a decision...
" choices that in this case arise because of complementarities.
Mathematical proof of inconsistency
Using the values above and a utility function U(W), where W is wealth, we can demonstrate exactly how the paradox manifests.Because the typical individual prefers 1A to 1B and 2B to 2A, we can write conclude that the expected utilities of the preferred is greater than the expected utilities of the second choices, or,
Experiment 1
Experiment 2
We can rewrite the latter equation (Experiment 2) as
which contradicts the first bet (Experiment 1), which shows the player prefers the sure thing over the gamble.