Prospect theory
Encyclopedia
Risk
Risk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
i.e. where the probabilities of outcomes are known. The model is descriptive: it tries to model real-life choices, rather than optimal decision
Optimal decision
An optimal decision is a decision such that no other available decision options will lead to a better outcome. It is an important concept in decision theory. In order to compare the different decision outcomes, one commonly assigns a relative utility to each of them...
s.
Model
The theory was developed by Daniel KahnemanDaniel Kahneman
Daniel Kahneman is an Israeli-American psychologist and Nobel laureate. He is notable for his work on the psychology of judgment and decision-making, behavioral economics and hedonic psychology....
, a professor at Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
's Department of Psychology
Princeton University Department of Psychology
The Princeton University Department of Psychology, located in Green Hall, is an academic department of Princeton University on the corner of Washington St. and William St. in Princeton, New Jersey. For over a century, the department has been one of the most notable psychology departments in the...
, and Amos Tversky
Amos Tversky
Amos Nathan Tversky, was a cognitive and mathematical psychologist, a pioneer of cognitive science, a longtime collaborator of Daniel Kahneman, and a key figure in the discovery of systematic human cognitive bias and handling of risk. Much of his early work concerned the foundations of measurement...
in 1979 as a psychologically
Psychology
Psychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
more accurate description of preferences compared to expected utility theory
Expected utility hypothesis
In economics, game theory, and decision theory the expected utility hypothesis is a theory of utility in which "betting preferences" of people with regard to uncertain outcomes are represented by a function of the payouts , the probabilities of occurrence, risk aversion, and the different utility...
. It describes how people choose between probabilistic alternatives and evaluate potential losses and gain
Gain (finance)
In finance, gain is a profit or an increase in value of an investment such as a stock or bond. Gain is calculated by fair market value or the proceeds from the sale of the investment minus the sum of the purchase price and all costs associated with it...
s. In the original formulation the term prospect referred to a lottery
Lottery
A lottery is a form of gambling which involves the drawing of lots for a prize.Lottery is outlawed by some governments, while others endorse it to the extent of organizing a national or state lottery. It is common to find some degree of regulation of lottery by governments...
.
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
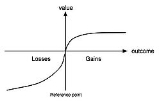
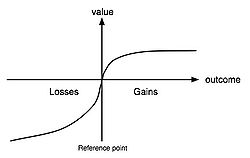
. In particular, people decide which outcomes they see as basically identical, set a reference point and then consider lesser outcomes as losses and greater ones as gains. In the following evaluation phase, people behave as if they would compute a value (utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
), based on the potential outcomes and their respective probabilities, and then choose the alternative having a higher utility.
The formula that Kahneman and Tversky assume for the evaluation phase is (in its simplest form) given by
,where
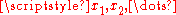are the potential outcomes and 
their respective probabilities. 
is a so-called value function that assigns a value to an outcome. The value function (sketched in the Figure) that passes through the reference point is s-shaped and asymmetrical. Losses hurt more than gains feel good (loss aversionLoss aversion
In economics and decision theory, loss aversion refers to people's tendency to strongly prefer avoiding losses to acquiring gains. Some studies suggest that losses are twice as powerful, psychologically, as gains....
). This differs greatly from expected utility theory, in which a rational agent is indifferent to the reference point. In expected utility theory, the individual only cares about absolute wealth, not relative wealth in any given situation. The function
is a probability weighting function and expresses that people tend to overreact to small probability events, but underreact to medium and large probabilities.To see how Prospect Theory (PT) can be applied in an example, consider the decision to buy insurance. Assuming the probability of the insured risk is 1%, the potential loss is $1,000 and the premium is $15. If we apply PT, we first need to set a reference point. This could be the current wealth or the worst case (losing $1,000). If we set the frame to the current wealth, the decision would be to either pay $15 for sure (which gives the PT-utility of
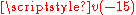) or a lottery with outcomes $0 (probability 99%) or −$1,000 (probability 1%) which yields the PT-utility of 
. These expressions can be computed numerically. For typical value and weighting functions, the latter expression could be larger due to the convexity of 
in losses, and hence the insurance looks unattractive. If we set the frame to −$1,000, both alternatives are set in gains. The concavity of the value function in gains can then lead to a preference for buying the insurance.We see in this example that a strong overweighting of small probabilities can also undo the effect of the convexity of
in losses: the potential outcome of losing $1,000 is overweighted.The interplay of overweighting of small probabilities and concavity-convexity of the value function leads to the so-called fourfold pattern of risk attitudes: risk-averse behavior in gains involving moderate probabilities and of small probability losses; risk-seeking behavior in losses involving moderate probabilities and of small probability gains.
Applications
Some behaviors observed in economicsEconomics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, like the disposition effect
Disposition effect
The disposition effect is an anomaly discovered in behavioral finance. It relates to the tendency of investors to sell shares whose price has increased, while keeping assets that have dropped in value...
or the reversing of risk aversion
Risk aversion
Risk aversion is a concept in psychology, economics, and finance, based on the behavior of humans while exposed to uncertainty....
/risk seeking in case of gains or losses (termed the reflection effect), can also be explained by referring to the prospect theory.
The pseudocertainty effect
Pseudocertainty effect
The pseudocertainty effect is a concept from prospect theory. It refers to people's tendency to perceive an outcome as certain while in fact it is uncertain...
is the observation that people may be risk-averse or risk-acceptant depending on the amounts involved and on whether the gamble relates to becoming better off or worse off. This is a possible explanation for why the same person may buy both an insurance
Insurance
In law and economics, insurance is a form of risk management primarily used to hedge against the risk of a contingent, uncertain loss. Insurance is defined as the equitable transfer of the risk of a loss, from one entity to another, in exchange for payment. An insurer is a company selling the...
policy and a lottery
Lottery
A lottery is a form of gambling which involves the drawing of lots for a prize.Lottery is outlawed by some governments, while others endorse it to the extent of organizing a national or state lottery. It is common to find some degree of regulation of lottery by governments...
ticket.
An important implication of prospect theory is that the way economic agents subjectively frame an outcome or transaction in their mind affects the utility they expect or receive. This aspect has been widely used in behavioral economics and mental accounting
Mental accounting
A concept first named by Richard Thaler , mental accounting attempts to describe the process whereby people code, categorize and evaluate economic outcomes....
. Framing and prospect theory has been applied to a diverse range of situations which appear inconsistent with standard economic rationality: the equity premium puzzle
Equity premium puzzle
The equity premium puzzle is a term coined in 1985 by economists Rajnish Mehra and Edward C. Prescott. It is based on the observation that in order to reconcile the much higher returns of stocks compared to government bonds in the United States, individuals must have implausibly high risk aversion...
, the excess returns puzzle and long swings/PPP puzzle of exchange rates through the endogenous prospect theory of Imperfect Knowledge Economics, the status quo bias
Status quo bias
The status quo bias is a cognitive bias for the status quo; in other words, people tend not to change an established behavior unless the incentive to change is compelling...
, various gambling and betting puzzles, intertemporal consumption
Intertemporal consumption
Economic theories of intertemporal consumption seek to explain people's preferences in relation to consumption and saving over the course of their life...
, and the endowment effect
Endowment effect
In behavioral economics, the endowment effect is a hypothesis that people value a good or service more once their property right to it has been established. In other words, people place a higher value on objects they own than objects that they do not...
.
Another possible implication for economics is that utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
might be reference based, in contrast with additive utility functions underlying much of neo-classical economics. This means people consider not only the value they receive, but also the value received by others. This hypothesis is consistent with psychological research into happiness
Happiness
Happiness is a mental state of well-being characterized by positive emotions ranging from contentment to intense joy. A variety of biological, psychological, religious, and philosophical approaches have striven to define happiness and identify its sources....
, which finds subjective measures of wellbeing are relatively stable over time, even in the face of large increases in the standard of living (Easterlin, 1974; Frank, 1997).
Military historian John A. Lynn argues that prospect theory provides an intriguing if not completely verifiable framework of analysis for understanding Louis XIV's foreign policy
Foreign policy
A country's foreign policy, also called the foreign relations policy, consists of self-interest strategies chosen by the state to safeguard its national interests and to achieve its goals within international relations milieu. The approaches are strategically employed to interact with other countries...
nearer to the end of his reign (Lynn, pp. 43–44).
Limits and extensions
The original version of prospect theory gave rise to violations of first-order stochastic dominanceStochastic dominance
Stochastic dominance is a form of stochastic ordering. The term is used in decision theory and decision analysis to refer to situations where one gamble can be ranked as superior to another gamble. It is based on preferences regarding outcomes...
. That is, prospect A might be preferred to prospect B even if the probability of receiving a value x or greater is at least as high under prospect B as it is under prospect A for all values of x, and is greater for some value of x. Later theoretical improvements overcame this problem, but at the cost of introducing intransitivity
Intransitivity
In mathematics, the term intransitivity is used for related, but different, properties of binary relations:- Intransitivity :A relation is transitive if, whenever it relates some A to some B, and that B to some C, it also relates that A to that C...
in preferences. A revised version, called cumulative prospect theory
Cumulative prospect theory
Cumulative prospect theory is a model for descriptive decisions under risk which was introduced by Amos Tversky and Daniel Kahneman in 1992 . It is a further development and variant of prospect theory...
overcame this problem by using a probability weighting function derived from Rank-dependent expected utility
Rank-dependent expected utility
The rank-dependent expected utility model is a generalized expected utility model of choice under uncertainty, designed to explain the behaviour observed in the Allais paradox, as well as for the observation that many people both purchase lottery tickets and insure against losses .A...
theory. Cumulative prospect theory can also be used for infinitely many or even continuous outcomes (e.g., if the outcome can be any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
).