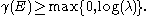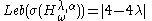Almost Mathieu operator
Encyclopedia
In mathematical physics
, the almost Mathieu operator arises in the study of the quantum Hall effect. It is given by
acting as a self-adjoint operator
on the Hilbert space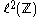
. Here 
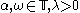are parameters. In pure mathematics, its importance comes from the fact of being one of the best-understood examples of an ergodic Schrödinger operator. For example, three problems (now all solved) of Barry Simon
's fifteen problems about Schrödinger operators "for the twenty-first century" featured the almost Mathieu operator.
For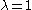
, the almost Mathieu operator is sometimes called Harper's equation.
is a rational number, then 
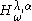
is a periodic operator and by Floquet theory its spectrum is purely
absolutely continuous.
Now to the case when
is irrational.
Since the transformation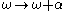
is minimal, it follows that the spectrum of 
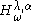does not depend on 
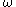. On the other hand, by ergodicity, the supports of absolutely continuous, singular continuous, and pure point parts of the spectrum are almost surely independent of 
.
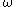It is now known, that
That the spectral measures are singular when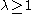
follows (through the work of Last and Simon)
from the lower bound on the Lyapunov exponent
given by
This lower bound was proved independently by Avron, Simon and Michael Herman, after an earlier almost rigorous argument of Aubry and André. In fact, when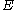
belongs to the spectrum, the inequality becomes an equality (the Aubry-André formula), proved by Jean Bourgain
and Svetlana Jitomirskaya.
Another striking characteristic of the almost Mathieu operator is that its spectrum is a Cantor set
for all irrational
and 
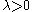. This was shown by Avila and Jitomirskaya solving the by-then famous "Ten Martini Problem" (also one of Simon's problems) after several earlier results (including generically
and almost surely
with respect to the parameters).
Furthermore, the measure of the spectrum of the almost Mathieu operator is known to be
for all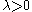
. For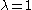 
this means that the spectrum has zero measure (this was first proposed by Douglas Hofstadter
and later became one of Simon's problems). For
, the formula was discovered numerically by Aubry and André and proved by Jitomirskaya and Krasovsky.
The study of the spectrum for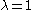
leads to the Hofstadter's butterfly
, where the spectrum is shown as a set.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the almost Mathieu operator arises in the study of the quantum Hall effect. It is given by
acting as a self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
on the Hilbert space
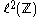. Here 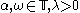are parameters. In pure mathematics, its importance comes from the fact of being one of the best-understood examples of an ergodic Schrödinger operator. For example, three problems (now all solved) of Barry SimonBarry Simon
Barry Simon is an eminent American mathematical physicist and the IBM Professor of Mathematics and Theoretical Physics at Caltech, known for his prolific contributions in spectral theory, functional analysis, and nonrelativistic quantum mechanics , including the connections to atomic and...
's fifteen problems about Schrödinger operators "for the twenty-first century" featured the almost Mathieu operator.
For
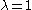, the almost Mathieu operator is sometimes called Harper's equation.The spectral type
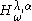
If is a rational number, then is a periodic operator and by Floquet theory its spectrum is purely
absolutely continuous.
Now to the case when
is irrational.Since the transformation
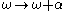is minimal, it follows that the spectrum of 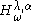does not depend on 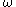. On the other hand, by ergodicity, the supports of absolutely continuous, singular continuous, and pure point parts of the spectrum are almost surely independent of 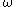.It is now known, that
- For
, 
has surely purely absolutely continuous spectrum. (This was one of Simon's problems.) - For
, 
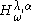has almost surely purely singular continuous spectrum. (It is not known whether eigenvalues can exist for exceptional parameters.) - For
, 
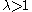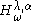has almost surely pure point spectrum and exhibits Anderson localizationAnderson localizationIn condensed matter physics, Anderson localization, also known as strong localization, is the absence of diffusion of waves in a disordered medium. This phenomenon is named after the American physicist P. W...
. (It is known that almost surely can not be replaced by surely.)
That the spectral measures are singular when
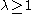follows (through the work of Last and Simon)from the lower bound on the Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
given by
This lower bound was proved independently by Avron, Simon and Michael Herman, after an earlier almost rigorous argument of Aubry and André. In fact, when
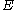belongs to the spectrum, the inequality becomes an equality (the Aubry-André formula), proved by Jean BourgainJean Bourgain
Jean Bourgain is a Belgian mathematician. He has been a faculty member at the University of Illinois, Urbana-Champaign and, from 1985 until 1995, professor at Institut des Hautes Études Scientifiques at Bures-sur-Yvette in France, and since 1994 at the Institute for Advanced Study in Princeton,...
and Svetlana Jitomirskaya.
The structure of the spectrum
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
for all irrational
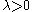and . This was shown by Avila and Jitomirskaya solving the by-then famous "Ten Martini Problem" (also one of Simon's problems) after several earlier results (including genericallyand almost surely
with respect to the parameters).
Furthermore, the measure of the spectrum of the almost Mathieu operator is known to be
for all
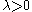. For 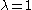this means that the spectrum has zero measure (this was first proposed by Douglas HofstadterDouglas Hofstadter
Douglas Richard Hofstadter is an American academic whose research focuses on consciousness, analogy-making, artistic creation, literary translation, and discovery in mathematics and physics...
and later became one of Simon's problems). For
, the formula was discovered numerically by Aubry and André and proved by Jitomirskaya and Krasovsky.The study of the spectrum for
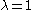leads to the Hofstadter's butterflyHofstadter's butterfly
Hofstadter's butterfly is the name of a fractal structure discovered by Douglas Hofstadter, which he described in 1976 in an article on the energy levels of Bloch electrons in magnetic fields. It gives a graphical representation of the spectrum of the almost Mathieu operator for \lambda = 1 at...
, where the spectrum is shown as a set.