
Almost flat manifold
Encyclopedia
In mathematics
, a smooth compact
manifold
M is called almost flat if for any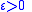 there is a Riemannian metric
there is a Riemannian metric  on M such that
on M such that 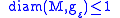 and
and
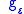 is
is  -flat, i.e. for sectional curvature of
-flat, i.e. for sectional curvature of 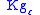 we have
we have 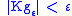 .
.
In fact, given n, there is a positive number such that if a n-dimensional manifold admits an
such that if a n-dimensional manifold admits an 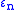 -flat metric with diameter
-flat metric with diameter 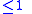 then it is almost flat. On the other hand you can fix the bound of sectional curvature and finally you get the diameter going to zero, so the almost flat manifold is a special case of a collapsing manifold
then it is almost flat. On the other hand you can fix the bound of sectional curvature and finally you get the diameter going to zero, so the almost flat manifold is a special case of a collapsing manifold
, which is collapsing along all directions.
According to the Gromov—Ruh theorem, M is almost flat if and only if it is infranil. In particular, it is a finite factor of a nilmanifold
, which is the total space of a principal torus bundle over a principal torus bundle over a torus.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a smooth compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M is called almost flat if for any
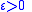 there is a Riemannian metric
there is a Riemannian metric  on M such that
on M such that 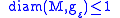 and
and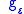 is
is  -flat, i.e. for sectional curvature of
-flat, i.e. for sectional curvature of 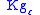 we have
we have 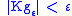 .
.In fact, given n, there is a positive number
 such that if a n-dimensional manifold admits an
such that if a n-dimensional manifold admits an 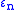 -flat metric with diameter
-flat metric with diameter 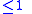 then it is almost flat. On the other hand you can fix the bound of sectional curvature and finally you get the diameter going to zero, so the almost flat manifold is a special case of a collapsing manifold
then it is almost flat. On the other hand you can fix the bound of sectional curvature and finally you get the diameter going to zero, so the almost flat manifold is a special case of a collapsing manifoldCollapsing manifold
In Riemannian geometry, a collapsing or collapsed manifold is an n-dimensional manifold M that admits a sequence of Riemannian metrics gn, such that as n goes to infinity the manifold is close to a k-dimensional space, where k In Riemannian geometry, a collapsing or collapsed manifold is an...
, which is collapsing along all directions.
According to the Gromov—Ruh theorem, M is almost flat if and only if it is infranil. In particular, it is a finite factor of a nilmanifold
Nilmanifold
In mathematics, a nilmanifold is a differentiable manifold which has a transitive nilpotent group of diffeomorphisms acting on it. As such, a nilmanifold is an example of a homogeneous space and is diffeomorphic to the quotient space N/H, the quotient of a nilpotent Lie group N modulo a closed...
, which is the total space of a principal torus bundle over a principal torus bundle over a torus.

